九年级第一学期期末考试数学试题
一．选择题(每小题3分，共24分)
01．方程x2+4x+4=0的根的情况是（ ）。
A、有两个不相等的实数根 B、有两个相等的实数根
C、有一个实数根 D、没有实数根
02．如图所示，该几何体的主视图是（ ）。
 |
03．关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0，则a的值为（ ）。
A、1 B、-1 C、1或-1 D、0.5
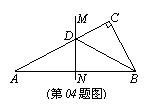
04．如图，在△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连结BD，若cos∠BDC=
，则BC的长是（ ）。
A、4cm B、6cm C、8cm D、10cm
05．在□ABCD中，对角线AC和BD相交于点O，如果AC=10，BD=12，AB=m，那么m的取值范围是（ ）。
A、2＜m＜22 B、1＜m＜11 C、10＜m＜12 D、5＜m＜6
06．如图，两个标有数字的轮子分别被等分为4部分和3部分，它们可以分别绕轮子中心旋转，旋转停止时，每个轮子上方的箭头各指着轮子上的一个数字，这两个数字的和为偶数的概率是（ ）。
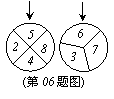
A、
B、
C、
D、
07．在平面直角坐标系中，若A(a，6)、B(2，a)、C(0，2)三点在同一条直线上，则a的值为（ ）。
A、4或-2 B、4或-1 C、-4或1 D、-4或2
08．如图，有一矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F，则△CEF的面积为（ ）。
A、4 B、6 C、8 D、10
二．填空题(每小题3分，共24分)
09．台湾是我国最大的岛屿，总面积为35989.76km2，这个数用科学记数法表示(保留两位有效数字)为 。
10．计算(1+
)0+(
)-1+2cos30°= 。
11．已知反比例函数
的图象分布在第二、四象限，则一次函数y=kx+b中，y随x的增大而 (填“增大”、“减小”、“不变”)。
12．一天晚上，某人在路灯下距路灯竿6米远时，发现他在地面上的影子是3米长，则当他离路灯竿10米远时，他的影子长是 米。
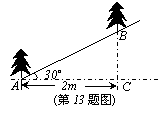
13．如图，沿倾斜角为30°的山坡植树，要求相邻两颗树间的水平距离AC为2m，那么相邻两棵树的斜坡距离AB约为
m(结果精确到0.1m，
≈1.732，≈1.414)。
 | |||||
 | |||||
 |
14．已知：a2+a-1=0，则a3+2a2+2006= 。
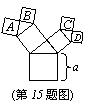
15．如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm，则正方形A、B、C、D的面积之和为 cm2。
16．如图是我市将要开发的一块长方形的土地，长为xkm，宽为3km，建筑开发商将这块土地分为甲、乙、丙三部分，其中甲和乙均为正方形，现计划甲地建住宅区，乙地建商业区，丙地开辟成小区公园，若已知丙地的面积为2km2，则x的值为 。
三．解答题(共9个小题，满分72分)
17．用适当方法解下列方程(每小题5分，共10分)
(1)x2-10x+25=7 (2)(x-1)2+2x(x-1)=0
18．(4分)楼房、旗杆在路灯下的影子如图所示，试确定路灯灯泡的位置，再作出小树在路灯下的影子。(不写作法，保留作图痕迹)
 |
19．(6分)在围棋盒中有x颗黑色棋子和y颗白色棋子，从盒中随机地取出一个棋子，如果它是黑色棋子的概率是
。
(1)试写出y与x的函数关系式；
(2)若往盒中再放进10颗黑色棋子，则取得黑色棋子的概率变为
，求x和y的值。
20．(8分)如图，在△ABC中，AC=BC，∠C=90°，AD是∠BAC的角平分线，DE⊥AB，垂足为E。
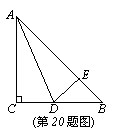(1)已知CD=
，求AC的长；
(2)求证：AB-AC=CD。
21．(8分)如果点P是x轴正半轴上的一个动点，过点P作x轴的垂线PA，交双曲线
于点A，连接OA。
(1)如图①，当点P在x轴的正方向上运动时，Rt△AOP的面积大小是否变化？若不变，请求出Rt△AOP的面积；若改变，试说明理由；
(2)如图②，在x轴上点P的右侧有一点D，过点D作x轴的垂线交双曲线于点B，连结BO交AP于点C。设△AOC的面积为S1，梯形BCPD的面积为S2，则S1与S2大小关系是S1 S2(填“＞”或“＜”或“=”)。
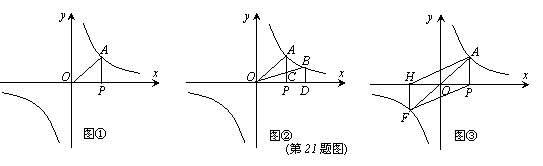(3)如图③，AO的延长线与双曲线
的另一个交点为F，FH垂直于x轴，垂足为点H，连结AH、PF，求四边形APFH的面积。
22．(8分)一艘渔船在A处观测到东北方向有一小岛C，已知小岛C周围4.8海里范围内是水产养殖场。渔船沿北偏东30°方向航行10海里到达B处，在B处测得小岛C在北偏东60°方向，这时渔船改变航行向正东(即BD)方向航行，这艘渔船是否有进入养殖场的危险？
23．(8分)某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克。经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克。现该商场要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应涨价多少元？
24．(10分)我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形。请解答下列问题：
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；
(2)探究：当等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和与其中一条对角线的大小关系，并证明你的结论。
25．(10分)如图，菱形ABCD的边长为24厘米，∠A＝60°，点P从点A出发沿线路AB→BD作匀速运动，点Q从点D同时出发沿线路DC→CB→BA作匀速运动。
(1)求BD的长；
(2)已知点P、Q运动的速度分别为4厘米/秒，5厘米/秒，经过12秒后，P、Q分别到达M、N两点，若按角的大小进行分类，请你确定△AMN是哪一类三角形，并说明理由；
(3)设(2)中的点P、Q分别从M、N同时沿原路返回，点P的速度不变，点Q的速度改变为a厘米/秒，经过3秒后，P、Q分别到达E、F两点，若△BEF与(2)中的△AMN相似，试求a的值。