九年级数学第二学期阶段性测试（一）
试 卷
亲爱的同学：
好的开端是成功的一半，希望你们稳扎稳打，在考试中获得好成绩！
请注意：全卷共三大题25小题，满分150分。
一、选择题。（本题有12小题，每小题4分，共48分）
1、下列运算正确的是（ ）
A、a+a=a2 B、a2·a=2a3 C、(2a)2÷a=4a D、(―ab)2=―ab2
2、我县经济发展步伐不断加快，综合实力显著增强，其中外向型经济发展迅速，近四年来实际利用外资1640万美元。1640万美元用科学记数法表示为（ ）
A、1.64×103美元 B、1.64×107美元 C、0.164×108美元 D、164×105美元
3、计算
的结果为（ ）
A、4
B、
C、
D、16
4、若等腰三角形底角为72°，则顶角为（ ）
A、108° B、72° C、54° D、36°
5、不等式2―x<1的解是（ ）
A、x>1 B、x>―1 C、x<1 D、x<―1
6、夏天，一杯开水放在桌子上，杯中水的温度T（℃）随时间t变化的关系大致图象（ ）
T（℃）
T（℃）
T（℃） T（℃）
O t O t O t O t
A B C D
7、在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（ ）
A、小明的影子比小强的影子长
B、小明的影子比小强的影子短
y
C、小明的影子和小强的影子一样长 D、无法判断谁的影子长
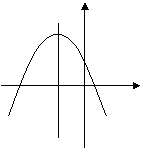
8、已知抛物线y=―x2+bx+c的部分图象如图所示，若y<0，
则x的取值范围是（ ）
A、―2.5<x<
B、―1.5<x<
-1 0 x
C、x>或x<—2.5 D、x<或x>—2.5
y
9、如图，AP切圆O于点P，OA交圆O于B，且AB=1，
P
AP=
，则阴影部分的面积S等于（ ）
O
B
A
A、
B、
C、
D、无法确定
10、如图，把一个正方形纸片三次对折后沿虚线剪下（1）、（2）两部分，则展开（2）得（ ）
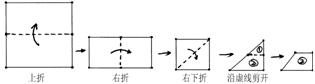
A B C D
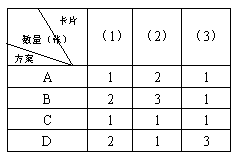11、有若干张如图所示的正方形和长方形卡片，表中所列四种方案能拼成邻边长分别是a+b和2a+b的矩形是（ ）
a （1） b （2） b （3）
a b a
12、已知P是线段AB的黄金分割点，点P将AB分成m、n两部分（m>n），以m为边长的正方形面积是S1，以（m+n）和n为边长的矩形的面积为S2，则S1与S2的大小关系是（ ）
A、S1>S2 B、S1=S2 C、S1<S2 D、无法确定
二、填空题。（本题6小题，每小题5分，共30分）
13、在等式3×□－2×□=15的两个方格内分别填入一个数，使这两个数是互为相反数且等式成立，则第一个方格内的数是________。
A
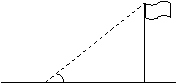
14、小辉想知道校园内旗杆的高（如右图），他测得CB=10m，
∠ACB=50°，请你帮他算出旗杆高AB约________米
（保留三个有效数字）。（注：旗杆垂直于地面，供选数据： 50°
sin50°≈0.766，cos50°≈0.643，tan50°≈1.192） c B
15、从标有1、3、4、6、8的五张卡片中随机抽取两张，和为偶数的概率是________。
16、甲乙两种糖果，售价分别为20元/千克和24元/千克，根据市场调查发现，将这两种糖果按一定比例混合后销售，取得了较好的销售效果。现在糖果的售价有了调整：甲种糖果的售价上涨了8%，乙种糖果的售价下降了10%，如果这两种混合糖果的售价恰好保持不变，那么甲、乙糖果的混合比例应为_________。
17、如图，若把四根木条钉成的矩形木框变形为平行四边形ABCD
A D
的形状，并使面积为矩形的一半，则这个平行四边形的一个最
小内角的值等于________。 B C
18、在一列数1、2、3、4、……、1000中，数字0出现的次数共是_____次。
三、解答题。（本题有7题，共72分。）
19、（8分）（1）计算：
（2）解方程：2x2―4x―5=0
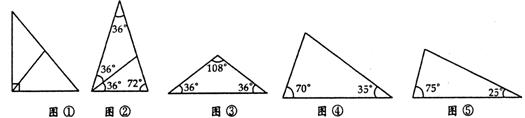
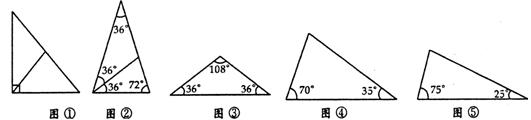
20、(10分)我们知道：直角三角形斜边上的中线等于斜边的一半,说明斜边上的中线可把直角三角形分成两个等腰三角形(图①)。又比如,顶角为36°的等腰三角形也能分成两个等腰三角形（图②）。
（1）试试看，你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗？
（2）△ABC中，有一内角为36°，过某一顶点的直线将△ABC分成两个等腰三角形，则满足上述条件的不同形状（相似的认为是同一形状）的△ABC最多有5种，除了图②、图③中的两种，还有三种，请你画出来。
21、（8分）阅读材料：符号“
”称为二阶行列式，规定它的运算法则为：
= ad―bc，例如 
的计算方法为 =2×3－4×5=―14。
请根据阅读材料完成：
x 
（1）化简二阶行列式 x2―1 1
（2）若 
=1003，试求代数式4a―2b+2007的值。
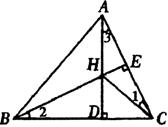
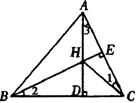22、（12分）已知：如图△ABC中，高AD和BE相交于点H，且HA=HC。
（1）求证：∠1=∠2。
（2）用直尺和圆规画出经过B、H、C三点的⊙O（不写画法）。
（3）证明EC是⊙O的切线。
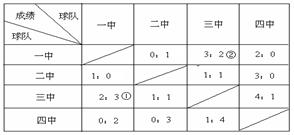23、（本题10分）下表是某市4所中学举行男子足球单循环赛的成绩登记表．表中①与②表示的是同一场比赛，在这场比赛中一中进了3个球，三中进了2个球，即一中以3：2胜三中，或者说三中以2：3负于一中,其余依次类推．按照比赛规则胜一场得3分,平一场得1分,负一场得0分．
（1）本次足球单循环赛共进行了几场比
赛？你能排出他们的名次吗？
（2）求各场比赛的平均进球数；
（3）求各场比赛进球数的众数和中位数．
24、（12分）光华农机租赁公司共有50台联合收割机，其中甲型20台，乙型30台。现将这50台联合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区。
两地区与该农机租赁公司商定的每天的租赁价格见下表：
| 每台甲型收割机的租金 | 每台乙型收割机的租金 | |
| A地区 | 1800元 | 1600元 |
| B地区 | 1600元 | 1200元 |
（1）设派往A地区x台乙型联合收割机，租赁公司这50台联合收割机一天获得的租金为y（元），求y与x间的函数关系式，并写出x的取值范围；
（2）若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来；
（3）如果要使这50台联合收割机每天获得的租金最高，请你为光华农机租赁公司提出一条合理建议。
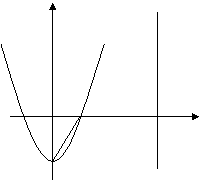
25、（12分）如图，二次函数y=2x2―2的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，直线x=m（m>1）与x轴交于点D（直线x=m平行于y轴）。
（1）求A、B、C三点坐标。
（2）在直线x=m(m>1)上有一点P（点P在第一象限内），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求P的坐标。（用含m的代数式表示）。
（3）在（2）成立的条件下，试问：抛物线y=2x2―2上是否存在一点Q，使得四边形ABPQ为平行四边形？若存在这样的点Q，请求出m的值；若不存在，请说明理由。
y
A O B D x
C x=m
九年级数学第二学期阶段性测试（一）答题卷
一、选择题。（本题有12小题，每小题4分，共48分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题。（本题6小题，每小题5分，共30分）
13、______ 14、______ 15、______ 16、______ 17、______ 18、_____
三、解答题。（本题有7题，共72分）
19、(8分)
(1)计算： (2)解方程：2x2―4x―5=0
20、（10分）
（1）
（2）
21、（8分）（1）
（2）
22、（12分）（1）
 |
（2）
（3）
23、（10分）（1）（4分）
（2）（3分）
（3）（3分）
24、（12分）（1）
（2）
（3）
25、（12分）（1）
（2）
（3）
数学参考答案
一、选择题。（本题有12小题，每小题4分，共48分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | C | D | A | B | D | C | C | A | D | B |
二、填空题。（本题6小题，每小题5分，共30分）
13、3 14、11.9 15、
16、3∶2 17、30° 18、192
三、解答题。（本题7小题，共72分）
19、（8分）
（1）计算：
解原式=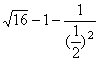
= 4―1―4 ……………… 3分
= ―1 ……………………1分
（2）解方程：2x2―4x―5=0
解法一：这里a=2，b=―4，c=―5
b2―4ac = (―4)2―4×2×(―5) = 16+40 = 56 ………………1分
∴x=
………………………2分
∴x1=
，x2=
………………………………1分
解法二：x2―2x=
……………………1分
x2―2x+1=+1
(x―1)2=
……………………2分
∴x―1=±
∴x1=1+
，x2=1― …………1分
20、（10分）（1）正确画出图③、④、⑤各得2分。
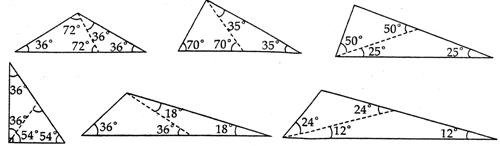
（2）画出第一种得2分，第二种1分，第三种1分。
21、（8分）
x
（1）解 x2―1 1
=x·1―(x2―1)· ………………2分
=x―(x+1)(x―1)· …………… 1分
=x―(x+1)=―1 …………………………1分
（2）根据 = 1003得：b―2a = 1003 …… 1分
原式=2(2a―b)+2007
=2×(―1003)+2007 ……………………2分
=―2006+2007=1 ………………………1分
22、证明：（1）在△AHC中，
∵HA=HC
∴∠1=∠2 ………………1分
∵AD⊥BC，BE⊥AC，∠AHE=∠BHD，
∴∠3=∠2 ………………2分
∴∠1=∠2 ………………1分
（2）画图正确即得4分。
（3）连结CO并延长交⊙O于F，连结FH，则
∠F+∠FCH=90° ………………2分
由（1）知∠1=∠2
∵∠F=∠2
∴∠F=∠1 ………………1分
∴∠1+∠FCH=90°
∴EC⊥FC，EC是⊙）的切线 …………1分
23、（1）（4分）6场比赛；一中、二中、三中、四中的得分分别是6分、7分、4分、0分。
所以二中是第一名，一中是第二名，三中是第三名，四中是第四名。
（2）（3分）平均进球数为：
（1+5+2+2+3+5）=3（球）
（3）（3分）各场比赛进球数的众数为2和5，中位数是25。
24、（1）若派往A地区的乙型收割机为x台，则派往A地区的甲型收割机为（30―x）台；派往B地区的乙型收割机为（30―x）台，派往B地区的甲型收割机为（x―10）台。
∴y=1600x+1800 (30―x)+1200 (30―x)+1600 (x―10)
=200x+74000 …………3分
x的取值范围是：10≤x≤30（x为t整数） …………1分
（2）由题意得200x+74000≥79600 ………………2分
解得x≥28，又10≤x≤30
∴x取28、29、30这三个值。
∴有3种分配方案 ……………………1分
①当x=28时，即派往A地区甲型收割机2台，乙型28台；
派往B地区甲型收割机18台，乙型2台。
②当x=29时，即派往A地区甲型收割机1台，乙型29台；
派往B地区甲型收割机19台，乙型1台。
③当x=30时，即30台乙型收割机全部派往A地区；
20台甲型收割机全部派往B地区。 ………………2分
（3）由于一次函数y=200x+74000的y值随x增大而增大，所以
当x=30时，y取得最大值， y取大值=200×30+74000=80000元 ……………2分
即建议农机租赁公司将30台乙型收割机全部派往A地区；20台甲型收割机全部派往B地区，可使公司获得的租金最高。 ………………1分
25、（12分）
解：（1）令y=0，得2x2―2=0，解得x=±1 ………………2分
点A坐标为（―1，0），点B为（1，0） …………1分
令x=0，得y=―2，所以C点坐标为（0，―2） ……1分
（2）①当△PDB∽△COB时，有
∵BD=m－1，OC=2，OB=1
∴
∴PD=2（m－1）
∴P1（m，2m－2） ………………2分
②当△PDB∽△BOC时，
∴
∴PD=（m―1）=m―
∴P2=（m，
） ………………2分
（3）假设抛物线y=2x－2上存在一点Q，使得四边形ABPQ为平行四边形
∴PQ=AB=2，点Q的横坐标为m―2
当P1为（m，2m―2）时，点Q1坐标为（m―2，m―2）
∵点Q1在抛物线y=2x2－2的图象上
∴2m―2=2(m―2)2―2
整理为m2―5m+4=0
∴m1=4，m2=1（舍去） …………………………2分
当P2为（m，）
∵点Q2在抛物线上
化为4m2―17m+13=0
解得m3=
，m4=1（舍去） ……………………2分
∴m的值为4，