九年级数学第二学期期中素质检测卷
卷一
一.选择题（本题有10小题，每小题4分，共40分。每小题只有一个选项是正确的，不选、错选、多选均不给分）
1.实数3的相反数 （ ）
A． 
B．
C．3 D．-3
2.2006年国民经济持续快速增长，嘉兴市人均GDP突破5000美元。据省统计局初步核算，全市地区生产总值约1343亿元，用科学记数法表示为（ ）元
A．
B．
C．
D．
3.下列图形中，既是轴对称图形又是中心对称图形的是( )
 |
4. 函数
中,自变量x的取值范围是( )
A. 
B. 
C. 
D. 
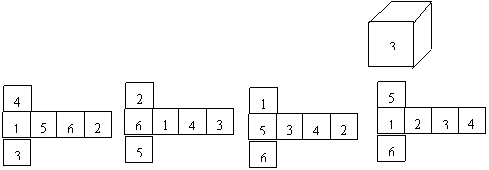5. 如图：正方体的六个面标有1，2，3，4，5，6六个数字，而且相对两个面的数字之和相等，下列各图是它的展开图的是（ ）
2
1
A B C D
6. 如果2m, 1-m, 3m这三个实数在数轴上所对应的点从左到右依次排列, 那么m的取值范围是( )
A．
B．
C．
D．
７.李明想打开他的玩具保险箱,但是他忘记了该保险箱的密码,只记得该密码有2个数字且每个数字都在0至4(包括0和4)这个范围内,那么他第一次尝试便可打开保险箱的可能是( )
A．
B．
C． 
D． 
|
|
|
|
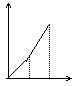
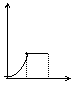
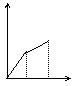
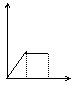
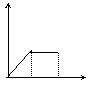v(千米/时)
| ||||||
|
| |||||
|
0 t1 t2 t (时) t1 t2 t (时) t1 t2 t (时) t1 t2 t (时) t1 t2 t (时)
A B C D
9.嘉兴乌镇旅游节期间, 几名同学租一辆面包车前去游览, 面包车的租价为180元, 出发时又增加了两名同学,结果每个同学比原来少分担了3元车费. 若设参加游览的同学共有x人, 则可得方程( )
A. 
B.
C. 
D.
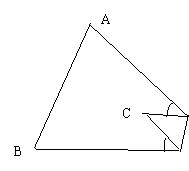
10. 三角形纸片ABC中,∠A=65°, ∠B=75°,
将纸片的一角折叠,使点C落在△ABC内,如图,
若∠1=20°,则∠2的度数为（ ）.
1
A. 60° B. 45° C. 40° D. 20°
2
卷二
二. 填空题（本题有6小题，每小题5分，满分30分）
11. 分解因式:x2-4= .
12. 已知
,则代数式
的值是
.
13. 把抛物线
的图象向右平移2个单位,再向下平移3个单位,所得图象的解析式是
.
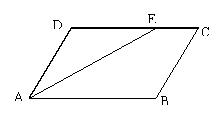
14.如图, ABCD中,AE平分∠DAB,∠B=100°,
y
则∠DAE= 度
x
(第14题图) (第15题图)
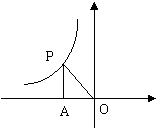
15.如图：反比例函数的图象上有一点P，PA⊥x轴于A，△AOP的面积为2，则反比例函数的解析式为 。
16.定义：用逗号将2个表达式连起来称为逗号表达式，它的一般表达式为：“表达式1，表达式2”，而整个逗号表达式的值等于表达式2的值：如“2+3，4+7”的值为11，现已知“a-b,a+b”的值为4；“a-2b, b”的值为7，
则“a+b,a+3b”= 。
三.解答题（共8题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17. 计算: 
18. 先化简代数式:
, 再取你自己喜欢的一个x的值代入这个代数式,并求出它的值。
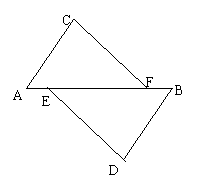
19.已知,如图,E,F是AB上的两点.AE=BF,
又因为AC∥DB,且AC=DB,,
求证: CF=DE.
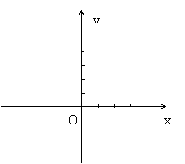20. 已知一次函数的图象经过点
和点
,完成下列各题:
(1) 在给定的坐标系中画出这个函数的图象;
(2) 求这个一次函数的解析式。
21.如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．
（1）在图1中，以格点为顶点画一个三角形，使三角形的三边长分别为3、
、2
．
（2）在图2中，线段AB的端点在格点上，请画出以AB为一边的三角形，使这个三角形的面积为6（要求至少画出3个）．
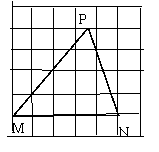
（3）在图3中，△MNP的顶点M、N在格点上，P在小正方形的边上，问这个三角形的面积相当于多少个小方格的面积？在你解出答案后，说说你的解题方法．
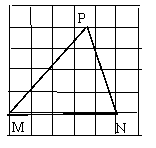
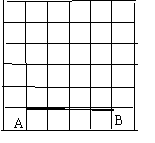
图1 图2 图3
22. 某风景区对5个旅游景点的门票价格进行了调整,根据统计调价前后各景点的游客人数基本不变,有关数据如下表所示:
| 景点 | A | B | C | D | E |
| 原价(元) | 10 | 10 | 15 | 20 | 25 |
| 现价(元) | 5 | 5 | 15 | 25 | 30 |
| 平均日人数(千人) | 1 | 1 | 2 | 3 | 2 |
（1）该景区称调整前后这5个景点的门票的平均收费不变,平均日收入持平,问风景区是怎样计算的?
（2）另一方面,游客认为调整收费后风景区的平均日收入相对于调价前实际上增加了约9.4℅,问游客是怎样计算的?
（3）你认为风景区和游客哪一个的说法比较能反映整体实际?
23. 如图,在直角坐标系中,以01
为圆心的⊙01与x轴交于C,D两点与y轴交于A,B两点,连结AC。
（1）点E在AB上,EA=EC,求证:
;
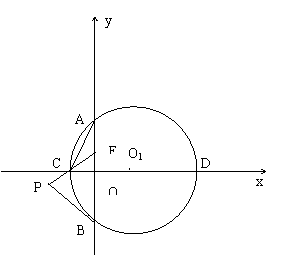（2）在(1)的结论下,延长EC到P,连结PB,若PB=PE,试判断PB与⊙01的位置关系,并说明理由;
（3）如果
,⊙01的半径为4,求(2)中点P的坐标。
24.某科技公司投资2000万元，成功研制并批量生产一种市场需要量很大的高科技替代产品，已知生产每件产品的成本为40元，在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量就减少1万件，销售单价为x(元)时，年销售量为y(万件)，年获利（年获利 = 年销售额 — 生产成本 — 投资）为z(万元)
⑴ 试写出y与x之间的函数关系式；
⑵ 试写出z与x之间的函数关系式 ；
⑶ 计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别是多少万件？
⑷ 公司计划：在第一年按年获利最大确定的销售单价进行销售；第二年年获利不低于1130万元，请你借助函数图象的性质，说明第二年的销售单价x(元)应确定在什么范围内？
九年级数学第二学期期中素质检测卷答卷
卷一
一.选择题 (本大题有10小题，每小题4分，满分40分）
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
卷二
二.填空题（本大题有6小题，每小题5分，满分30分）
11、 12、 13、
14、 15、 16、
三.解答题（共8题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17. 计算:
18. 先化简代数式:, 再取你自己喜欢的一个x的值代入这个代数式,并求出它的值。
 |
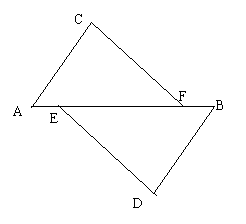19.已知,如图,E,F是AB上的两点.AE=BF,
又因为AC∥DB,且AC=DB,,
求证: CF=DE.
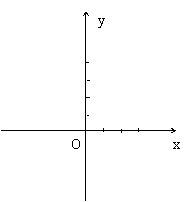20. 已知一次函数的图象经过点和点,完成下列各题:
(3) 在给定的坐标系中画出这个函数的图象;
(4) 求这个一次函数的解析式。
21.如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．
（1）在图1中，以格点为顶点画一个三角形，使三角形的三边长分别为3、、2．
（2）在图2中，线段AB的端点在格点上，请画出以AB为一边的三角形，使这个三角形的面积为6（要求至少画出3个）．
（3）在图3中，△MNP的顶点M、N在格点上，P在小正方形的边上，问这个三角形的面积相当于多少个小方格的面积？在你解出答案后，说说你的解题方法．
|
| |||||||||
图1 图2 图3
22. 某风景区对5个旅游景点的门票价格进行了调整,根据统计调价前后各景点的游客人数基本不变,有关数据如下表所示:
| 景点 | A | B | C | D | E |
| 原价(元) | 10 | 10 | 15 | 20 | 25 |
| 现价(元) | 5 | 5 | 15 | 25 | 30 |
| 平均日人数(千人) | 1 | 1 | 2 | 3 | 2 |
(1) 该景区称调整前后这5个景点的门票的平均收费不变,平均日收入持平,问风景区是怎样计算的?
(2) 另一方面,游客认为调整收费后风景区的平均日收入相对于调价前实际上增加了约9.4℅,问游客是怎样计算的?
(3) 你认为风景区和游客哪一个的说法比较能反映整体实际?
23. 如图,在直角坐标系中,以01为圆心的⊙01与x轴交于C,D两点与y轴交于A,B两点,连结AC。
(1)
点E在AB上,EA=EC,求证:;
(2)
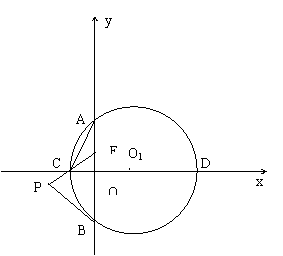在(1)的结论下,延长EC到P,连结PB,若PB=PE,试判断PB与⊙01的位置关系,并说明理由;
(3)
如果,⊙01的半径为4,求(2)中点P的坐标。
24.某科技公司投资2000万元，成功研制并批量生产一种市场需要量很大的高科技替代产品，已知生产每件产品的成本为40元，在销售过程中发现：当销售单价定为100元时，年销售量为20万件；销售单价每增加10元，年销售量就减少1万件，销售单价为x(元)时，年销售量为y(万件)，年获利（年获利 = 年销售额 — 生产成本 — 投资）为z(万元)
⑴ 试写出y与x之间的函数关系式；
⑵ 试写出z与x之间的函数关系式 ；
⑶ 计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别是多少万件？
⑷ 公司计划：在第一年按年获利最大确定的销售单价进行销售；第二年年获利不低于1130万元，请你借助函数图象的性质，说明第二年的销售单价x(元)应确定在什么范围内？