初三数学第一学期期末模拟测试
班级 姓名 学号 成绩
一、选择题:(本题共30分,每小题3分)
在每题的四个备选答案中只有一个是正确的,请将正确答案前的字母填在括号中.
1、 已知两圆的半径分别为3和5,且它们的圆心距为8,则这两个圆的位置关系为( )
(A) 外离 (B)外切 (C)相交 (D)内含
2、
已知数据3,5,![]() ,10的平均数是6,则
,10的平均数是6,则![]() 的值为( )
的值为( )
(A)4 (B)5 (C)6 (D)7
3、在图形“圆,平行四边形,矩形,正方形”中,既是轴对称图形又是中心对称图形的有( )
 (A)一个 (B)两个 (C)三个 (D)四个
(A)一个 (B)两个 (C)三个 (D)四个
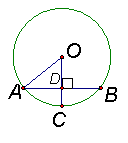
4、如图,已知![]() 中,半径
中,半径![]() 垂直于弦
垂直于弦![]() ,垂足为
,垂足为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5、下列方程中,为一元二次方程的是 ( )
(A) ![]() (B)
(B) ![]()
(C)![]() (D)
(D) ![]()
 6.如图5,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中数据,计算耕地的面积为
6.如图5,在宽为20m,长为30m的矩形地面上修建两条同样宽的道路,余下部分作为耕地. 根据图中数据,计算耕地的面积为
(A) 600m2 (B) 551m2
(C) 550 m 2 (D) 500m2
7.一元二次方程![]() 的根的情况是( )
的根的情况是( )
(A)有两个相等的实数根 (B)有两个不相等的实数根 (C) 无实数根(D)不能确定
8.若圆锥的母线长为4cm,底面半径为3cm,则圆锥的侧面展开图的面积是( )
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() ;
;
 9.如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )
9.如图,⊙O中,弦AD∥BC,DA=DC,∠AOC=160°,则∠BCO等于( )
(A)20°; (B)30°; (C)40°; (D)50°;
10.设计一个商标图案:先作矩形ABCD,使AB=2BC,AB=8,再以点A为圆心、AD的长为半径作半圆,交BA的延长线于F,连FC。图中阴影部分就是商标图案,该商标图案的面积等于( )
(A)4π+8;(B)4π+16;(C)3π+8;(D)3π+16;
二、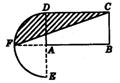 填空题:(本题共18分,每空3分)
填空题:(本题共18分,每空3分)
1、已知一个圆形细菌的直径长约为![]() 那么
那么
这个细菌的直径长用科学记数表示为 米.
2、已知分式![]() 的值为零,那么
的值为零,那么![]() 的值为
.
的值为
.
3、若方程![]() 是关于
是关于![]() 的一元二次方程,则
的一元二次方程,则![]() 的取值范围是 .
的取值范围是 .
4、投掷一枚质地均匀的骰子(它是一种各面上分别标有点数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的正方体的玩具),掷一次得到点数为“
的正方体的玩具),掷一次得到点数为“![]() ”的概率为
.
”的概率为
.
5、有一张圆形的纸片,如果不借助作图工具找它的圆心,你的方法是 .
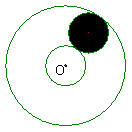 6、如图,这是一个滚珠轴承的示意图,其中内、外圆的半径分别为
6、如图,这是一个滚珠轴承的示意图,其中内、外圆的半径分别为![]() 和
和![]() ,如果在内、外圆之间放半径为2的滚珠(有阴影的圆表示滚珠),请你猜想在内、外圆之间最多可以放
个滚珠.
,如果在内、外圆之间放半径为2的滚珠(有阴影的圆表示滚珠),请你猜想在内、外圆之间最多可以放
个滚珠.
三、解答题:(本题共30分,每小题6分)
1、解方程![]() .
.
解:
2、计算: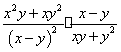 .
.
解:
3、计算:![]() .
.
解:
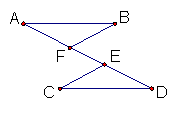 4、已知:如图,
4、已知:如图,![]() ∥
∥![]() ,
,![]() ,
,![]() .
.
求证:△![]() ≌△
≌△![]() .
.
证明
:
5、已知:如图,点![]() 是
是![]() 平分线
平分线![]() 上一点,
上一点,![]() .
.
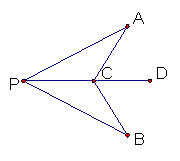 求证:
求证:![]() .
.
证明:
四、作图与解答题:(本题8分)
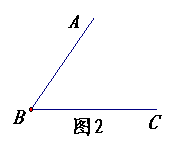
已知:如图,![]() .(作图要求保留作图痕迹)
.(作图要求保留作图痕迹)
(1)
求作:![]() ,使
,使![]() ;(2分)
;(2分)
(2)
求作:![]() 的平分线
的平分线![]() ;(2分)
;(2分)
(3)
如图(3),![]() 是
是![]() 的平分线
的平分线![]() 上任意一点,以
上任意一点,以![]() 为圆心的⊙O与
为圆心的⊙O与![]() 相切于
相切于
![]() 点.说明⊙O与
点.说明⊙O与![]() 相切.(4分)
相切.(4分)
五、解答题:(本题10分,每小题5分)
1、已知关于![]() 的方程
的方程![]() 的一个根为
的一个根为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:
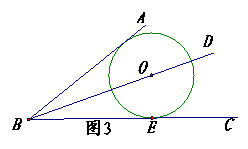
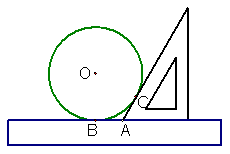 2、已知:如图,为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有
2、已知:如图,为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有![]() 角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点
角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点![]() 、点
、点![]() ),若量得
),若量得![]() ,试求圆的半径以及BC的弧长.
,试求圆的半径以及BC的弧长.
解
六、(本题24分,每小题8分)
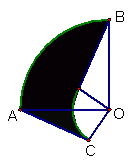 1、已知:如图,扇形
1、已知:如图,扇形![]() 与扇形
与扇形![]() 有一部分叠放在一起,且它们的圆心角都是
有一部分叠放在一起,且它们的圆心角都是![]() ,连结
,连结![]() 、
、![]() ,若
,若![]() ,
,![]() ,求阴影部分的面积.
,求阴影部分的面积.
解:
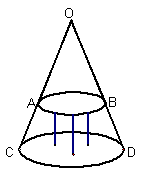 2、如图,这是圆桌正上方的灯泡
2、如图,这是圆桌正上方的灯泡![]() (把灯泡看作一个点),发出的光线照射在桌面后在地面上形成阴影的示意图,已知桌面直径为
(把灯泡看作一个点),发出的光线照射在桌面后在地面上形成阴影的示意图,已知桌面直径为![]() 米,桌面距地面
米,桌面距地面![]() 米,若灯泡离地面
米,若灯泡离地面![]() 米,求地面上阴影部分的面积.
米,求地面上阴影部分的面积.
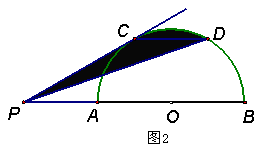
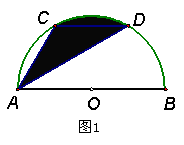
3、已知![]() 是半圆的直径,
是半圆的直径,![]() ∥
∥![]() ,
,![]() ,求:(1)如图1,若
,求:(1)如图1,若![]() 、
、![]() 是半圆上的三分之一点,求阴影部分的面积;(2)如图2,若点
是半圆上的三分之一点,求阴影部分的面积;(2)如图2,若点![]() 是
是![]() 延长线上的点,
延长线上的点,![]() 是切线,当其他条件不变时,说明此图中的阴影部分的面积与图1中阴影部分面积之间的关系.
是切线,当其他条件不变时,说明此图中的阴影部分的面积与图1中阴影部分面积之间的关系.
 解:
解:
参考答案
一、 选择:
1、B 2、C 3、C 4、D 5、D 6、B 7、A 8、B 9、B 10、A
二.填空:
1、1.5×10-5 2.X=![]() 3.m≠-2
4、
3.m≠-2
4、![]() 5、略 6、6
5、略 6、6
三、解答题:
1、解:x2-x+3x-3=0
x2+2x-3=0
(x+3)(x-1)=0
x1=-3 x2=1
2.原式=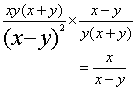
3.原式=9-3×9+1=-17
4.证明:∵AB∥CD∴∠A=∠D
∵AE=DF ∴AF=DE
∵AB=CD
∴△ABF≌△CDE
5.证明:因为AC平分∠APB所以∠APC=∠BPC
又因为PA=PB,所以△APC≌△BPC(SAS)
所以∠ACP=∠BCP
所以∠ACD=∠BCD
四、作图题:(略)
五、
1.解:∵关于X的方程3x2-(m+1)x-2=0的一个根为2
∴3×22-2(m+1)-2=0
∴m=4
将m=4代入4a2-4am+m2+m-2b=0得
4a2-16a+16+4-2b=0
∴(2a-4)2+4-2b=0
∴2a-4=0,4-2b=0
a=2,b=2
∴(ab)m=(2×2)4=256
2.解:连结OA,OB,OC
∵AB,AC分别切圆O于点B,C
∴OB⊥AB,OC⊥AC
∴∠BAC=120
∴∠OAB=60 ∠ BAC=60
∵AB=5
∴OB=5![]()
∴![]() 的长=
的长=![]()
六、1.解:∵∠AOD+∠BOD=∠AOD+∠AOC=90°
∴∠ BOD=∠AOC
又∵OA=OB,OC=OD
∴△AOC≌△BOD
S阴=S扇形OAB-S扇形OCD=![]()
2.解:设阴影部分的直径为d,由题意得
![]()
解得:d=2
S阴=![]() 2=
2=![]() 2=
2=![]()
3.解:(1)连结OC,OD
∵AB∥CD
∴ S△ACD=S△OCD
∴S阴=S扇形OCD
∵C,D是半圆上的三分之一点
∴∠COD=60°
∴S扇形OCD=![]()
(2)连结AC,AD
∵ AB∥CD
∴S△PCD=S△ACD
∴其它条件不变时,两图中的阴影部分面积相等