初三数学二模试卷
一、选择题（每小题3分，共30分，每小题给出4个答案，其中只有一个正确，把所选答案的编号写在题目前面的括号内）
1. 25的算术平方根是
A. 5 B.
±5 C.
D.
±
2. 计算
的结果是
A. 3 B. 9 C. －3 D. －9
3. 甲、乙两个样本，甲样本的方差是0.105，乙样本的方差是0.055，那么样本
A. 甲的波动比乙的波动大
B. 乙的波动比甲的波动大
C. 甲、乙的波动大小一样
D. 甲、乙的波动大小无法确定
4. 小明家新买了一台17英寸液晶电脑显示器，则下列表示该显示器厚度数据的是
A. 6毫米 B. 6厘米 C. 6分米 D. 6米
5. 如图，A、B两点被池塘隔开，在AB外任选一点C，连结AC、BC分别取其三等分点M、N量得MN=38m。则AB的长是
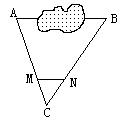
A. 76m B. 104m C. 114m D. 152m
6. 在湖笔文化节前，为美化城市，需在绿化带上放置一定数量的圆柱形花柱，花柱底面直径1.2米，高为3米，则一个花柱的侧面积是
A. 
B.
C. 
D.
7. 如果两圆有且只有两条公切线，那么这两个圆的位置关系是
A. 外离 B. 外切 C. 相交 D. 内切
8. 一个给定的三角形被平行于一边的直线截成一个小三角形和一个梯形，若小三角形和梯形的面积分别是y和x，则y关于x的函数图形大致为
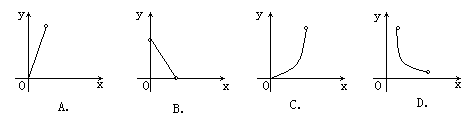
9. 某市政府计划2年内将市区人均住房面积由现在的a平方米提高到b平方米。设每年人均住房面积增长率为x，则x满足的方程是
A. 
B. 
C. 
D. 
10. 如图，在一次函数
的图象上取点P，作PA⊥x轴，PB⊥y轴；垂足为B，且矩形OAPB的面积为2，则这样的点P个数共有
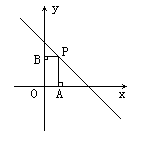
A. 1 B. 2 C. 3 D. 4
二、填空题（每小题3分，共30分）
11. 3的相反数是____________。
12. 函数
的自变量x的取值范围是____________。
13. 方程
的根为____________。
14. 已知反比例函数的图像经过点（－2，－4），则它的解析式为____________。
15. △ABC中，∠A=50°，∠B=60°，则∠C=____________度。
16. 不等式
的最大整数解是____________。
17. 如图，在△ABC中，∠ACB=90°，BC=6，AB=9，CD⊥AB，则BD=____________。
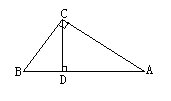
18. 如图，已知∠1=∠2，若再增加一个条件就能使结论“AB：AD=BC：DE”成立，则这个条件可以是____________。
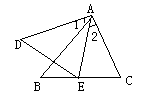
19. 如图，⊙O的半径为3cm，过直径BA延长线上一点P，作直线分别交⊙O于C、D，若C是PD中点，且PC=2PA，则PA=____________cm。
20. 已知直线
与x轴、y轴分别交于点A和点B，过B点的抛物线
的顶点为C，如果△ABC恰为等边三角形，则b的值为____________。
三、解答题（共60分）
21. （本小题满分8分）
计算：
22. （本小题满分8分）
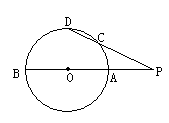
解方程组：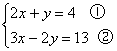
23. （本小题满分10分）
已知，如图，正方形ABCD中，E为CD边上一点，F为BC延长线上一点，且CE=CF，
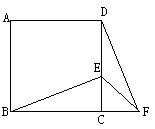
（1）求证：△BCE≌△DCF
（2）若∠FDC=28°，求∠BEF的度数。
24. （本小题满分10分）
新新广告公司将一块广告牌制作任务交给师徒二人，已知师傅单独完成这项任务比徒弟单独完成少用2天，现由徒弟先做1天，师徒再合作2天可完成。
（1）求：师徒二人单独完成这项任务各需几天？
（2）广告牌任务完成后得报酬540元，师徒二人按底薪（基本工资）加工作量进行分配：即每人每天底薪若干元，余下按每人实际完成工作量分配，最后师徒二人所得报酬相同。现已知徒弟每天底薪20元，问师傅每天底薪多少元？
25. （本小题满分12分）
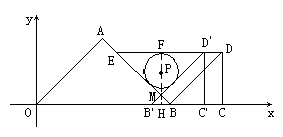
如图1，在x轴正半轴上以OB为斜边、BC为直角边向第一象限分别作等腰Rt△AOB和等腰Rt△CDB。OA=8，BC=4，在∠ABD内有一半径为1，且与AB、BD相切的⊙P。
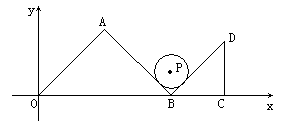
图1
（1）直接写出⊙P的圆心坐标为：________________；
（2）若△CDB在x轴上以每秒2个单位的速度向左匀速平移，⊙P同时相应在BA和BD上滑动，且保持与BA、BD相切，至⊙P终止运动，设运动时间为t秒，试用含t的代数式表示P点坐标；并证明P点的横、纵坐标之和为定值；
（3）如图2，过D点作x轴的平行线交AB于E，D'B'与AB交于M，在满足（2）的前提下，t取何值时，⊙P可成为△D'EM的内切圆。
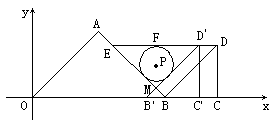
图2
26. （本小题满分12分）
已知，抛物线
过点P（1，－2）、Q（－1，2），且与x轴交于A（x1，0）、B（x2，0）两点（A在B左侧），与y轴交于C点。
（1）填空：b的值为___________，a与c的关系式是：___________。
（2）若
，且
（O为坐标原点），求抛物线的解析式；（可直接使用（1）中的结论）；
（3）若抛物线的顶点为点M，是否存在开口向下的抛物线，使得△MAB的外接圆半径为
？若存在，求出抛物线的解析式；若不存在，请说明理由。
四、自选题（两小题，共10分）
27. （本小题满分3分）
已知，抛物线（其中a为负整数）经过点A（－1，4）及点B（2，1），且与x轴有两个交点，则
的最小值为___________。
28. （本小题满分7分）
如图，△ABC是圆内接正三角形，D是BC弧上任意一点，试探求线段BD、DC、DE之间的关系并予证明。
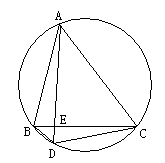
[参考答案]
一、选择题
1. A 2. C 3. D 4. B 5. C
6. A 7. C 8. B 9. C 10. D
二、填空题
11. －3 12. x≠1
13. 
14. 
15.
70
16. 9 17. 4
18. ∠B=∠D
19. 
20.
三、解答题：
21. 解：原式
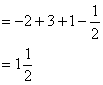
22. 解：①×2+②得
把代入①式，得
∴方程组的解为
23. （1）证：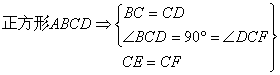 
（2）
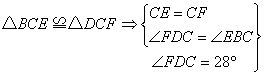
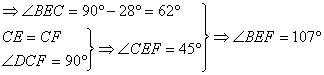
24. 解：（1）设师徒二人单独完成这项任务分别需x天、y天
则：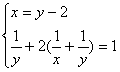
解得：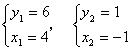
（经检验不合题意舍去）
答：师徒二人单独完成这项任务分别需4天、6天。
（2）设师傅每天底薪z元，则
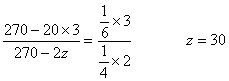（元）
答：师傅每天的底薪为30元。
25. （1）（
）
（2）运动t秒时，B'B=2t，△BMB'仍为等腰直角三角形。
过M作MH⊥x轴于H，MH=t
∴OH=
，
∴P点坐标为（
）
P点横、纵坐标之和为
定值。
（3）若⊙P为△D'EM的内切圆
则FM+MH=DC
即
∴当时，⊙P可成为△D'EM的内切圆。
26. （1）－2 a+c=0
当x=1时，有
①
当x=－1时，有
②
①－②得
，①+②得
（2）若
∴抛物线在x轴的两交点必有：
又∵
∵，∴
，
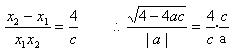
∴抛物线为：
（3）若△MAB的外接圆的半径为，则
∴存在为
或
27. 解：∵，过A（－1，4），B（2，1）
∴
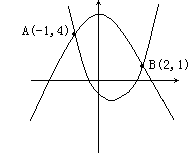
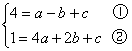
①－②得
∴
∴
，∴当a=－1时，
最小值=5。
28. 
证：延长CD至H，使DH=BD，△ABC为正三角形，
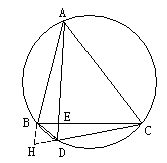
∴∠BDC=120°，∴△DBH为正三角形，
∴BD+DC=HC
又可证：△ABD≌△CBH，
∴BD+DC=HC=AD
又∵可证：△ABD∽△CED
∴
∴
∴
∴