初三数学期末复习试卷(1)
一、选择题
1.下列计算正确的是( )
(A) ![]() =0 (B)
=0 (B)![]() =-15
(C)
=-15
(C)![]() (D)
(D) ![]()
2. 下列各式![]() ,
,![]() ,
,![]() ,
,![]() 中,分式的个数是( )
中,分式的个数是( )
(A)0 (B)1 (C)2 (D) 3
3. 下列语句中表示命题的是( )
(A) 画一条线段. (B) 作线段AB的垂直平分线.
(C) 等边三角形是中心对称图形吗? (D) 平行四边形对角线相等.
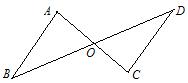 4. 如图,已知O是线段AC和BD的中点,要说明△ABO≌△CDO,以下回答最合理的是(
)
4. 如图,已知O是线段AC和BD的中点,要说明△ABO≌△CDO,以下回答最合理的是(
)
(A) 添加条件∠A=∠C
(B) 添加条件AB=CD
(C) 不需要添加条件
(D) △ABO和△CDO不可能全等
5.“从布袋中取出一个红球的概率为0”,这句话的含义是( )
(A) 布袋中红球很少 (B) 布袋中没有球
(C) 布袋中没有红球 (D) 不能确定
6.在下列考察中,是抽样调查的是( )
(A) 了解全校学生人数 (B) 调查某厂生产的鱼罐头质量
(C) 调查苏州市出租车数量 (D) 了解全班同学的家庭经济状况
7. 若方程![]() 的一个根为
的一个根为![]() ,则k及另一个根的值为( )
,则k及另一个根的值为( )
(A)
7 ,3 (B) -7,3 (C) ![]() ,6 (D)
,6 (D) ![]() ,6
,6
8. 已知两圆的半径分别为8和5,圆心距为5,那么这两圆的位置关系是( )
(A) 内切 (B) 外切 (C) 相交 (D) 外离
9. 如图,已知∠BPC=50°,∠ABC=60°,则∠ACB是( )
(A) 40° (B) 50° (C) 60° (D) 70°
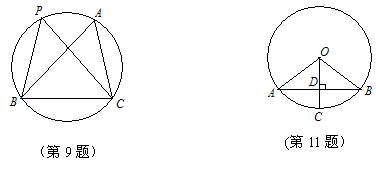
10.方程![]() 的左边配成完全平方后所得方程为 ( )
的左边配成完全平方后所得方程为 ( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
11. 如图,已知⊙O中,半径OC垂直于弦AB,垂足为D,若OD=3,OA=5,则AB的长为( )
(A) 2 (B) 4 (C) 6 (D) 8
12. 下面几个抽样调查选取样本的方法合理的有( )
(1)为调查我国的人均国民收入状况,只在苏州市进行调查;
(2)为估计苏州市中考数学成绩,抽取所有学号尾数是0和5中考学生进行调查;
(3)为调查苏州市中学生的健康状况,共调查10名中学生的健康状况.
(A) 0个 (B) 1个 (C) 2个 (D) 3个
13. 甲盒中有红球2只,白球1只,乙盒中有白球2只,红球1只,某人随机从甲盒或乙盒中摸出一只球,该球恰好是甲盒中白球的概率是( )
(A)![]() ( B)
( B)![]() (C)
(C)![]() (D)
(D)![]()
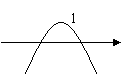
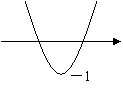
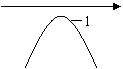
14.
|
|
|
|
 | |||||||
 | |||||||
 | |||||||
|
|
|
|
|
|
|
|
(A ) (B ) (C) ( D)
15.已知两圆的半径分别为1和4,圆心距为3,则两圆的公切线的条数是( )
(A)1 (B)2 (C)3 (D)4
 二、填空题
二、填空题
16. 当![]() ________时,分式
________时,分式![]() 的值小于零。
的值小于零。
17.方程![]() 的解是
.
的解是
.
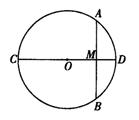
18. 如图,CD是⊙O的直径,CD⊥AB于M,已知AB=8,MD=2,
 则⊙O的半径为___________。
则⊙O的半径为___________。
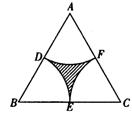
19. 如图,在边长为1的等边三角形ABC中,分别以三个顶点为圆心,![]() 长 为半径画弧交三边于D、E、F,则图中阴影部分的面积是______。
长 为半径画弧交三边于D、E、F,则图中阴影部分的面积是______。
20.一圆锥的底面半径为2cm,母线长为5cm,则此圆锥的侧面积为 .
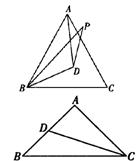 21. 如图,已知D为等边△ABC内的一点,AD=BD,∠DBP=∠DBC,BA=BP,则∠BPD=_________度。
21. 如图,已知D为等边△ABC内的一点,AD=BD,∠DBP=∠DBC,BA=BP,则∠BPD=_________度。
22. 如图,在△ABC中,∠A=2∠B,CD平分∠ACB,且AC=4cm,AD=2cm,则BC=__________cm。
23. 如下图左,图①为装有1黑、1白、1黄三只球的不透明方盒,图②为一转盘(转盘被分成相等的3个扇形区域)。甲、乙两人做游戏,若甲“摸、转同色”(如从盒中摸出黑球并且转盘转动后指针也停止在黑色区域,则甲胜);若甲“摸、转不同色”(如从盒中摸出黑球但转盘转动后指针停止在白色区域,则乙胜),你认为此游戏公平吗?答:__________(填“公平”或“偏向于谁”)
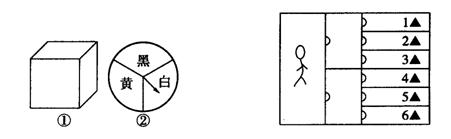
24. 如上图右,某人进入迷宫,迷宫中有8扇门,6个按钮,其中3号按钮为迷宫开关,则此人一次就能打开迷宫开关的概率是__________。
三、解答题
25. 计算:![]()
26. 解方程: ![]()
27. 化简求值:![]() ,其中
,其中![]()
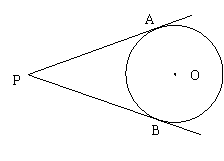 28. 如图所示,PA、PB是⊙O的切线,A、B为切点,
28. 如图所示,PA、PB是⊙O的切线,A、B为切点,![]() ,点C是⊙O上不同于A、B的任意一点,求
,点C是⊙O上不同于A、B的任意一点,求![]() 的度数。
的度数。
29. x1,x2是关于x的一元二次方程x2-kx+k-1=0的两个实数根,求y=( x1-2x2)( 2x1-x2)的最小值。
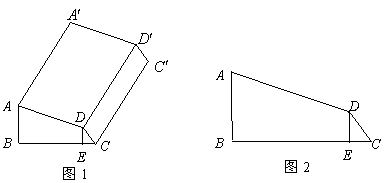
30. 小明家准备建造长为28米的蔬菜大棚,示意图如图(1).它的横截面为如图(2)所示的四边形![]() ,已知
,已知![]() 米,
米,![]() 米,
米,![]() ,
,![]() ,
,![]() 到
到![]() 的距离
的距离![]() 为1米.矩形棚顶
为1米.矩形棚顶![]() 及矩形
及矩形![]() 由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
 (下列数据可供参考
(下列数据可供参考![]() )
)
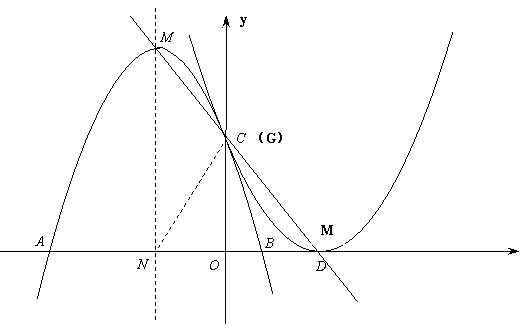
31. 已知抛物线![]() 与y轴的交点为C,顶点为M,直线CM的解析式
与y轴的交点为C,顶点为M,直线CM的解析式![]() 并且线段CM的长为
并且线段CM的长为![]()
(1) 求抛物线的解析式。
(2) 设抛物线与x轴有两个交点A(x1 ,0)、B(x2 ,0),且点A在B的左侧,求线段AB的长。
(3) 若以AB为直径作⊙N,请你判断直线CM与⊙N的位置关系,并说明理由。
 |
参考答案
一、1---5 DADCC 6---10 BBCDA 11---15 DBDCA
二、 16. ![]() 或
或![]() 17.
17. ![]() 18. 5 19.
18. 5 19. ![]()
20. ![]()
![]() 21. 30(提示:连结DC) 22. 6(提示:在CB上截取CE=CA,连结DE) 23. 偏向于乙 24.
21. 30(提示:连结DC) 22. 6(提示:在CB上截取CE=CA,连结DE) 23. 偏向于乙 24. ![]()
三、 25. ![]() 26.
26. ![]()
27.![]()
28. 连接OA、OB,在AB弧上任取一点C,
∵PA、PB是⊙O的切线,A、B为切点,连接AC、BC,
∴![]() ,
,
∵![]() ,在四边形OAPB中,可得
,在四边形OAPB中,可得![]()
(1) 若C点在劣弧AB上,则![]()
(2) 若C点在优弧AB上,则![]()
29.![]() ,故当k=
,故当k=![]() 时,y有最小值
时,y有最小值![]() 。
。
30.
过![]() 作
作![]() 于
于![]() ,
,

![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]() 总造价为
总造价为![]() (元).
(元).
31.
 |
(1)解法一:由已知,直线CM:y=-x+2与y轴交于点C(0,2)抛物线![]() 过点C(0,2),所以c=2,抛物线
过点C(0,2),所以c=2,抛物线![]() 的顶点M
的顶点M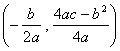 在直线CM上,所以
在直线CM上,所以![]()
若b=0,点C、M重合,不合题意,舍去,所以b=-2。即M![]()
过M点作y轴的垂线,垂足为Q,在![]()
所以,![]() ,解得,
,解得,![]() 。
。
∴所求抛物线为:![]() 或
或![]() (4分)以下同下。
(4分)以下同下。
(1)解法二:由题意得C(0 , 2),设点M的坐标为M(x ,y)
∵点M在直线![]() 上,∴
上,∴![]()
由勾股定理得![]() ,∵
,∵![]()
![]()
∴![]() =
=![]() ,即
,即![]()
解方程组 ![]() 得
得![]()
![]()
∴M(-2,4) 或 M‘ (2,0)
当M(-2,4)时,设抛物线解析式为![]() ,∵抛物线过(0,2)点,
,∵抛物线过(0,2)点,
∴![]() ,∴
,∴![]()
当M‘(2,0)时,设抛物线解析式为![]()
∵抛物线过(0,2)点,∴![]() ,∴
,∴![]()
∴所求抛物线为:![]() 或
或![]()
(2)∵抛物线与x轴有两个交点,
∴![]() 不合题意,舍去。
不合题意,舍去。
∴抛物线应为:![]()
抛物线与x轴有两个交点且点A在B的左侧,∴![]() ,得
,得
![]()
(3)∵AB是⊙N的直径,∴r =![]() , N(-2,0),又∵M(-2,4),∴MN = 4
, N(-2,0),又∵M(-2,4),∴MN = 4
设直线![]() 与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
与x轴交于点D,则D(2,0),∴DN = 4,可得MN = DN,∴
![]() ,作NG⊥CM于G,在
,作NG⊥CM于G,在![]()
![]() = r
= r
即圆心到直线CM的距离等于⊙N的半径
∴直线CM与⊙N相切