初三数学期末复习试卷(2)
一、选择题
1.方程![]() 的左边配成完全平方后所得方程为( )
的左边配成完全平方后所得方程为( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) 以上答案都不对
(D) 以上答案都不对
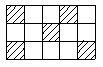 2.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
2.一只小狗在如图的方砖上走来走去,最终停在阴影方砖上的概率是( )
(A) (B) (C) (D)
3.利用尺规作图不能唯一作出三角形的是( )
(A) 已知三边 (B) 已知两边及夹角
(C) 已知两角及夹边 (D) 已知两边及其中一边的对角
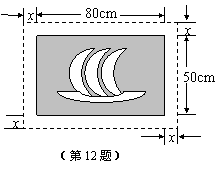 4. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色
4. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色
纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积
是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是( )
(A)x2+130x-1400=0 (B) x2+65x-350=0
(C) x2-130x-1400=0 (D) x2-65x-350=0
5. 用一把带有刻度的直角尺,
①可以画出两条平行的直线![]() 与
与![]() ,如图(1);②可以画出∠AOB的平分线OP,如图(2);
,如图(1);②可以画出∠AOB的平分线OP,如图(2);
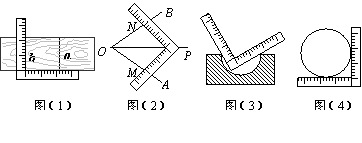 ③可以检验工件的凹面是否成半圆,如图(3);④可以量出一个圆的半径,如图(4).
③可以检验工件的凹面是否成半圆,如图(3);④可以量出一个圆的半径,如图(4).
上述四个方法中,正确的个数是( )
(A)1个 (B)2个 (C)3个 (D)4个
6.⊙O的半径为3,⊙A的半径为1,OA=2, 那么⊙O与⊙A的位置关系是( )
(A) 外离 (B) 外切 (C) 内切 (D) 相交
7. 如图甲,在正方形铁皮上剪下一个圆形和扇形,使之恰好围城图乙所示的一个圆锥模型。设圆的半径为r,扇形的半径为R,则圆的半径与扇形的半径之间的关系为( )
 (A) R=2r (B) R=
(A) R=2r (B) R=![]() r
r
(C)R=3r (D)R=4r
二、填空题
8.若分式![]() 的值为0,则x=
的值为0,则x=
 9.关于
9.关于![]() 的一元二次方程
的一元二次方程![]() 的一个根是0,则
的一个根是0,则![]() 的值为 。
的值为 。
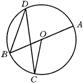
10.如图,在⊙O中,AB是⊙O的直径,∠D=40°,则∠AOC的度数为_____
11.二次函数 ![]() 的图像向下平移1个单位,得到的图像的表达式是
的图像向下平移1个单位,得到的图像的表达式是
 .
.
12.如图D、E是△ABC中BC边上的两点,AD=AE,请你
再附加一个条件
,使△ABE≌△ACD。
13.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平
放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按
如图所示的方法得到相关数据,进而可求得铁环的半径,若测得
PA=5cm,则铁环的半径是 cm。
三、解答题
14.计算:![]()
15.解方程:- =
16.已知x=2是方程x2-3x+m=0的一个根,则方程的另一个根和m的值。
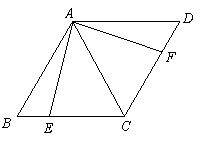
17.
如图,菱形![]() 中,
中,![]() 分别为
分别为![]() 上的点,且
上的点,且![]() .求证:
.求证:![]() .
.
 |
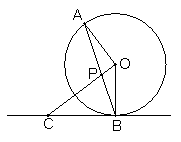 18.
如图,AB是⊙O的弦,CO⊥OA,OC交AB于点P,且PC=BC,BC是⊙O的切线吗?证明你的结论。
18.
如图,AB是⊙O的弦,CO⊥OA,OC交AB于点P,且PC=BC,BC是⊙O的切线吗?证明你的结论。
19.甲、乙两超市同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会,在一个纸盒里装有2个红球和2个白球,除颜色外,其它全部相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券的多少(如下表).
甲超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
乙超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
20. 如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;

 (2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
 |
21.已知抛物线![]() 经过
经过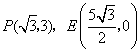 及原点
及原点![]() .
.
(1)求抛物线的解析式.
(2)过![]() 点作平行于
点作平行于![]() 轴的直线
轴的直线![]() 交
交![]() 轴于
轴于![]() 点,在抛物线对称轴右侧且位于直线
点,在抛物线对称轴右侧且位于直线![]() 下方的抛物线上,任取一点
下方的抛物线上,任取一点![]() ,过点
,过点![]() 作直线
作直线![]() 平行于
平行于![]() 轴交
轴交![]() 轴于
轴于![]() 点,交直线
点,交直线![]() 于
于![]() 点,直线
点,直线![]() 与直线
与直线![]() 及两坐标轴围成矩形
及两坐标轴围成矩形![]() (如图).是否存在点
(如图).是否存在点![]() ,使得
,使得![]() 与
与![]() 相似?若存在,求出
相似?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
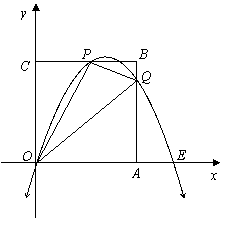 (3)如果符合(2)中的
(3)如果符合(2)中的![]() 点在
点在![]() 轴的上方,连结
轴的上方,连结![]() ,矩形
,矩形![]() 内的四个三角形
内的四个三角形![]() 之间存在怎样的关系?为什么?
之间存在怎样的关系?为什么?
参考答案
一、1---7 ABDBCCD
二、8. 1
9. -1 10.![]() 11.
11. ![]() 12. AB=AC…等 13.
12. AB=AC…等 13. ![]()
三、14. 4
15. ![]() 16.
1,2
16.
1,2
17. 答:BC是⊙O的切线
证明:∵PC=BC
∴∠CPB=∠CBP
又∵∠CPB=∠APO
∴∠APO=∠CBP
又∵BO=AO
∴∠OAB=∠OBA
∴∠APO+∠OAB=∠CBP+∠OBA
又∵OA⊥CO
∴∠APO+∠OAB=900
∴∠CBP+∠OBA=900
∴OB⊥BC
又∵CB过半径OB外端
∴CB是⊙O切线
18.因为四边形![]() 是菱形,所以
是菱形,所以![]()
因为![]() ,所以
,所以![]()
在![]() 与
与![]() 中,
中,
因为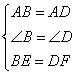 ,所以
,所以![]() 所以
所以![]() .
.
19.去甲超市购物一次摸奖获10元礼金券的概率是![]() (甲)
(甲)![]()
去乙超市购物一次摸奖获10元礼金券的概率是![]() (乙)
(乙)![]()
所以我选择去甲超市购物.
20.解:(1)BM=FN.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴ ∠ABD =∠F =45°,OB = OF.
又∵∠BOM=∠FON, ∴ △OBM≌△OFN .
∴ BM=FN.
(2)BM=FN仍然成立.
证明:∵△GEF是等腰直角三角形,四边形ABCD是正方形,
∴∠DBA=∠GFE=45°,OB=OF.∴∠MBO=∠NFO=135°.
又∵∠MOB=∠NOF, ∴ △OBM≌△OFN .∴ BM=FN.
21.解:(1)由已知可得:
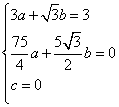 解之得,
解之得,![]() .
.
因而得,抛物线的解析式为:![]() .
.
(2)存在.
设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() ,要使
,要使![]() ,则有
,则有![]() ,即
,即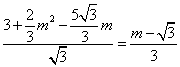 ,解之得,
,解之得,![]() .
.
当![]() 时,
时,![]() ,即为
,即为![]() 点,所以得
点,所以得![]()
要使![]() ,则有
,则有![]() ,即
,即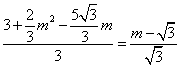
解之得,![]() ,当
,当![]() 时,即为
时,即为![]() 点,
点,
当![]() 时,
时,![]() ,所以得
,所以得![]() .故存在两个
.故存在两个![]() 点使得
点使得![]() 与
与![]() 相似.
相似.
![]() 点的坐标为
点的坐标为![]() .
.
(3)在![]() 中,因为
中,因为![]() .所以
.所以![]() .
.
当![]() 点的坐标为
点的坐标为![]() 时,
时,![]() .
.
所以![]() .
.
因此,![]() 都是直角三角形.
都是直角三角形.
又在![]() 中,因为
中,因为![]() .所以
.所以![]() .
.
即有![]() .
.
所以![]() ,又因为
,又因为![]()
![]() ,所以
,所以![]() .
.