解直角三角形测验
一、 选择题
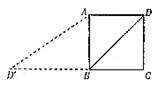
1、如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于（ ）
(A)．1 (B)．
(C)．
(D)．
2、如果
是锐角，且
，那么
的值是（ ）．
（A）
（B）
（C）
（D）
3、等腰三角形底边长为10㎝，周长为36cm，那么底角的余弦等于（ ）．
（A）
（B）
（C）
（D）
4、. 以下不能构成三角形三边长的数组是 ( )
（A）（1，
，2） （B）（，
，
） （C）（3，4，5） （D）（32，42，52）
5、在Rt△ABC中，∠C＝90°，下列式子中正确的是（ ）．
（A）
（B）
（C）
（D）
6、在矩形ABCD中，DE⊥AC于E，设∠ADE=
，且
,
AB = 4, 则AD的长为（ ）．
（A）3 （B）
（C）
（D）
7、某市在“旧城改造”中计划在一
块如图所示的三角形空地上种植某种草皮以美
化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（ ）．
（A）450a元 （B）225a元 （C）150a元 （D）300a元
8、已知α为锐角，tan（90°－α）=
，则α的度数为（ ）
（A）30° （B）45° （C）60° （D）75°
9、在△ABC中，∠C=90°，BC=5，AB=13，则sinA的值是( )
（A）
（B）
（C）
（D）
10、如果∠a是等边三角形的一个内角，那么cosa的值等于（ ）．
（A）
（B）
（C）
（D）1
二、 填空题
11、如图，在△ABC中，若∠A＝30°，∠B＝45°，AC＝
，
则BC＝
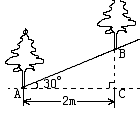12、如图，沿倾斜角为30°的山坡植树，要求相邻两棵树的水
平距离AC为2m，那么相邻两棵树的斜坡距离AB
为 m。(精确到0.1m)
13、离旗杆20米处的地方用测角仪测得旗杆顶的仰角为， 如果测角仪高为1.5米．那么旗杆的高为
米（用含的三角函数表示）．
14、校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米。一只小鸟从一
棵树的顶端飞到另一棵树的顶端，小鸟至少要飞__________米。
15、某校自行车棚的人字架棚顶为等腰三角形，
D是AB的中点，中柱CD = 1米，∠A=27°，
则跨度AB的长为 (精确到0.01米)。
三、 解答题
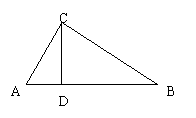16、已知：如图，在ΔABC中，∠ACB＝90°，CD⊥AB，垂足为D，若∠B＝30°，CD＝6，求AB的长．
17、如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为
，路基高度为5.8米，求路基下底宽（精确到0.1米）.
18、为申办2010年冬奥会，须改变哈尔滨市的交通状况。在大直街拓宽工程中，要伐掉一棵树AB，在地面上事先划定以B为圆心，半径与AB等长的圆形危险区，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°，树的底部B点的俯角为30°.
问：距离B点8米远的保护物是否在危险区内？
19、如图，某一水库大坝的横断面是梯形ABCD，坝顶宽CD＝5米，斜坡AD＝16
米，坝高 6米，斜坡BC的坡度
.求斜坡AD的坡角∠A（精确到1分）和坝底宽AB．（精确到0.1米）
20. 在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：
（1） 
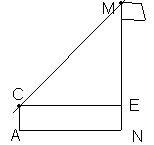在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；
（2） 量出测点A到旗杆底部N的水平距离AN＝m;
（3） 量出测倾器的高度AC＝h。
根据上述测量数据，即可求出旗杆的高度MN。
如果测量工具不变，请参照上述过程，重新设计一个方案测量某小山高度（如图2）
1）
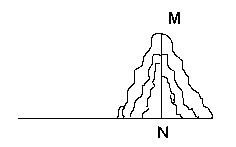在图2中，画出你测量小山高度MN的示意图
（标上适当的字母）
2）写出你的设计方案。 （（图2）
答案: 一、选择题
1、B 2、C 3、A 4、D 5、B 6、B 7、C 8、A 9、A 10、A
二、填空题
11、
12、2.3
13、1.5 +20tan 14、13 15、3.93米
三、解答题
16、8 17、18.1米
18、可求出AB= 4米
∵8＞4
∴距离B点8米远的保护物不在危险区内
19、 ∠A =22 01′ AB=37.8米
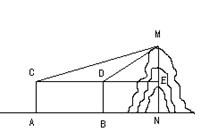
20、1）
2)方案如下：
（1） 测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；
（2） 测点B处安置测倾器，测得旗杆顶部M的仰角∠MDE＝
；
（3） 量出测点A到测点B的水平距离AB＝m;
（4） 量出测倾器的高度AC＝h。
根据上述测量数据可以求出小山MN的高度