初三数学第四次模拟试题及答案
一、填空题（本大题共10小题，每小题3分，共30分．）
1．
的倒数的相反数是 ．
2．若方程x2－2kx+3=0的一个根是3，则k= ．
3．若
互为相反数，则a2003+b2004= ．
4．因式分解x3－9x= ．
5．一次函数y=kx+b当x=0时，y＞0；当y=0时，x＜0，则此一次函数的图象不经过第 象限．
6．一组数据由3个4和5个9组成，则这组数据的平均数是 （精确到0．1）．
7．⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2相外切，则O1 O2= ．
8．如图，我们面向平面镜看到身后墙上的数字如下：
，那么转身后看身后墙上数字从左到右读为
.
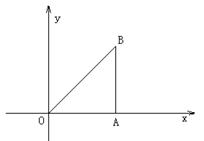
第9题图
9．如图，在直角坐标系中，点A（4，0），B（4，4），则线段AB 长为 ．
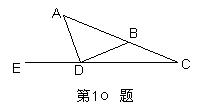
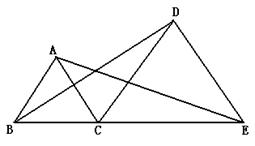
10． 如图：已知AD=DB=BC，∠C=250，则∠ADE = 度
二、选择题（本大题共6小题，每小题3分，共18分．把下列各题中唯一正确答案的序号填在题后的括号内．）
11．小强买了4本书，每本书的价格在18．95～24．95元之间，那么买这4本书花钱数为（ ）
（A）25～50元 （B）50～75元
（C）75～100元 （D）多于100元
12．点M（3－a，a+1）在第二象限，则a的取值范围是（ ）
（A）a＞－1 （B）－1＜a＜3
（C）a＜－1 （D）a＞3
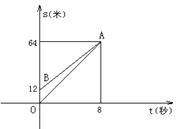
13．如图，OA、BA分别表示甲、乙两名学生运动的一次函数图象，图中s和t分别表示运动路程和时间，根据图象可以知道快者的速度比慢者的速度每秒快（ ）
（A）2．5米 （B）2米 （C）1．5米 （D）1米
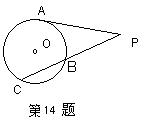
14．P是⊙O外一点，PA切⊙O于A，割线PBC
交⊙O于点B、C，若PB=BC=3，则PA的长是（ ）
（A）9 （B）3
（C）
（D）18
第13题图 第15题图
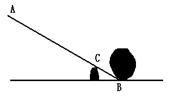
15．如图，用杠杆撬石头B时，C是支点，用力压杠杆A端时，杠杆绕C点转动，另一端B向上翘起，石头就被撬动，当B端向上翘10cm时，石头就能滚动，若AC：BC=5：1，要使石头能滚动，A端要下压（ ）
（A）100cm （B）60cm （C）50cm （D）10cm
16．一个形如圆锥冰淇淋纸筒，其底面直径为6cm，母线长为10cm，围成这样的冰淇淋纸筒所需纸片的面积是（ ）
（A）60
cm2 （B）30cm2
（C）28cm2
（D）15cm2
三、（本大题共4小题，每小题5分，共20分．）
17．先化简，再求值：
．其中a=－3．
18．某校初三学生在2004年物理、化学、生物实验操作考试中，成绩情况如图所示：
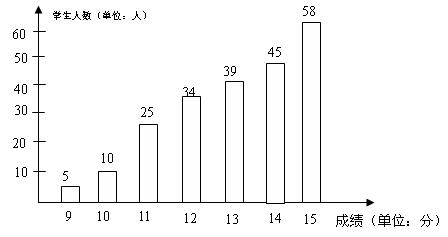
①该校初三学生在这次物理、化学、生物实验操作考试中，学生成绩的众数是＿＿＿，
②该校初三学生在这次物理、化学、生物实验操作考试中，学生成绩的平均数是＿＿＿，
③若确定得分在12分以上（含12分）的成绩为优秀，则该校初三学生成绩的优秀率是＿＿＿＿＿（保留两位有效数字）。
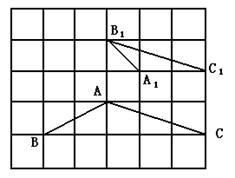
19．如图，在正方形网络上有两个三角形△A1B1C1和△ABC．
求证：△A1B1C1∽△ABC．
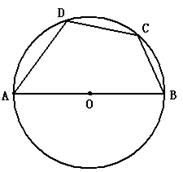
20．已知：如图，AB是⊙O的直径，弦BC=CD，∠A=50°，求∠B、∠C、∠D的度数．
四、（本大题共2小题，每小题8分，共16分．）
21． 如图，B、C、E三点在一条直线上，△ABC和△DCE均为等边三角形，连结AE、DB．（1）求证：AE=DB；（2）如果把△DCE绕点C顺时针再旋转一个角度，（1）中的结论还成立吗（只写出结论即可）？
22．（1）当k为何值时，一次函数
的图象与二次函数
的图象有两个交点.
（2）试写出k的一个数值，使这两个函数图象的交点的横坐标一个大于1，一个小于1.
五、（本大题共2小题，每小题8分，共16分．）
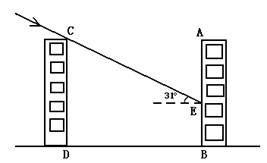
23．如图，小张家居住的甲楼AB面向正南，现计划在他家居住的楼前修建一座乙楼CD，楼高约为18米，两楼之间的距离为20米，已知冬天的太阳最低时，光线与水平线的夹角为31°．
（1）试求乙楼CD的影子落在甲楼AB上的高BE的长；（精确到0．01m）
（2）若让乙楼的影子刚好不影响甲楼，则两楼之间的距离至少应是多少米？（精确到0．01m）（参考数据：sin31°≈0。515，cos31°≈0.857,tan31°≈0.601）
24．某厂生产一种玩具赛车，成本为每辆16元，现有两种销售方式：第一种是直接由厂门市部销售，每辆售价为20元，但需每月支出固定费用是1500元；第二种是批发给文化用品及玩具模型商店销售，批发价为每辆18元，又知这两种销售方式均需缴纳税款为销售金额的5% 。
（1）求该厂这两种销售方式的月利润y（元）与售出辆数x（辆）的函数关系式；
（2）每月销售出多少辆车时，两种销售方式所获利润相等？
（3）若该厂今年5月份有1500辆，应如何安排销售就能获利最大？最大利润是多少？
六、（本大题共2小题，每小题10分，共20分．）
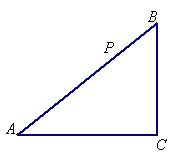
25．如图，在△ABC中∠C
=
.P为AB上一动点，且点P不与点A和B重合，过点P作PE⊥AB交AC 边(或者CB边)于E点，点E不与点C重合，可将△ABC分割成一个小三角形和一个四边形,若AB=5，AC = 4；设AP的长为x，分割的四边形的周长为y，
求y与x之间的函数关系式,并求出x的取值范围．
26. 已知:在直角坐标糸中，A、B两点是抛物线y=x2-（m-3）x-m与x轴的交点（A在B的右侧），x1, x2分别是A、B两点的横坐标, 且∣x1-x2∣=3.
（1）当m>0时，求抛物线的函数解析式.
（2）如果（1）中所求抛物线与y轴交于点C,问y轴上是否存在点D（不含与C重合的点）,使得以D、O、A为顶点的三角形与ΔAOC相似？若存在,请求出D点的坐标；若不存在,请说明理由。
（3）一次函数
y =kx+b的图象经过抛物线的顶点，且当 k>0 时，图象与两坐标轴所围成的面积是
，求一次函数的解析式。
数学第四次模拟考试答案
一、1．3 2．2 3．0 4．x(x+3)(x－3) 5．四 6．7．1 7．7 8． 12315 9． 4 10．75°
二、11．C 12．D 13．C 14．C 15．C 16．B
三、17．解：原式=
=
．当a=－3时，上式=
．
18．解： 15，13，81%
19．证明：AB=
，AC=
，BC=5，A1B1=
，A1C1=2，B1C1=，
∴
，∴△ABC∽△A1B1C1．
20．∠B=65°，∠C=130°，∠D=115°．
四、21．（1）证明：∵△ABC、△DCE均为正三角形，
∴BC=AC，DC=EC，∠ACB=∠DCE=60°．
∵∠BCD=60°+∠ACD，∠ACE=60°+∠ACD，∴∠BCD=∠ACE．
在△BCD和△ACE中，BC=AC，∠BCD=∠ACE，DC=EC，
∴△BCD≌△ACE．∴AE=DB．
（2）如果把△DCE绕点C顺时针再旋转一个角度，（1）中的结论仍成立．
22．解：由已知得，x2-9x-2k+2=0,△=81+8k-8>0,k>
,
设两交点横坐标为m,n,则有(m-1)(n-1)<0,mn-(m+n)+1<0,得-2k+2-9+1<0,
所以k>-3,所以k=略。
五、23．解：（1）过E作EG∥FD交CD于G点．
在Rt△CGE中，∵∠CEG=31°，
∴CG=CE·tan31°=20×0．6009=12．017（m）．∴BE=DG=CD－CG=5．983≈5．98（m）．
答：乙楼CD的影子落在甲楼AB的高约为5．98m．
（2）在Rt△CDF中，DF=CD·cot31°=18×1．644=29．957≈29．96（m）．
答：两楼之间的距离至少是29．96m．
24． （1）第一种销售方式：y=（4x+1500）(1-5%);即y=3.8x-1425
第二种销售方式：y=2x(1-5%),即y=1.9x
(2)当3.8x-1425=1.9x时，x=750,所以当每月销售750台时，两种方式获利相等
（3）当x=1500,按方案一，y=4275;按方案二，y=2850
所以按方案一获利最大，获利4275元。
六、25． 当E在AC上，PE:AP=3:4,AE:AP=5:4,四边形PECB周长y=12-x-5x/4+3x/4,
所以 y=-1.5x+12 (0<x<3.2)
当E在BC上时，四边形ACEP周长 y=12-PB-BE+PE,所以 y=
.(3.2<x<5)
26．解：(1) 由已知得 x1+x2=m-2,x1x2=-m,( x1+x2)-4 x1x2=9,得 （m-3）2+4m=0
m1=0,m2=2 因为m>0,所以 m=2.则解析式为 y=x2+x-2.
（2）由（1）知，A（1，0），B（-2，0），C（0，-2），
若相似，则OA：OD=OD：OA或OD=OC，所以有OD=
，或OD=2，
所以存在，D（0，2）或（0，
）或（0，）。
（3）抛物线的顶点坐标为（-，
），
=-k-b;
,解得b1=1,b2=-1.8,k1=2.5.k2=0.9
所以解析式为y=2.5x+1或y=0.9x-1