初三数学第一次模拟试试题
（考试时间：90分钟，满分：130分）
注意：1、本试卷分第一部分选择题和第二部分非选择题。
2、考生答卷前，必须将自己的姓名、考试号用黑色钢笔或圆珠笔填写地试卷和答题卡的相应位置，再用2B铅笔将考试号、科目涂在答题卡上相应的小框内
第一部分 选择题（共30分）
注意：考生必须将所选答案的字母标号用2B铅笔填涂到答题卡上相应的题号内，答在试卷上无效。
一、选择题：（每题给出四个答案，只有一个答案是正确的。每题3分，共30分。）
1．
的倒数是
（A）一3 （B）
（C）3 （D）
2、下列实数
，sin30°，0.1414，
中，无理数的个数是
A、2个 B、3个 C、4个 D、5个
3、等腰三角形一边长为4，一边长9，它的周长是
A、17 B、22 C、17或22 D、13
4．若a＞0，b＜－2，则点（a，b＋2）应在（ ）
（A）第一象限 （B）第二象限 （C）第三象限
（D）第四象限
5．(03台湾)下列为四个二次函数的图形，哪一个函数在x=2时有最大值3? ( )
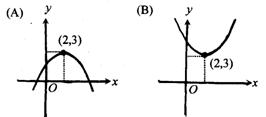
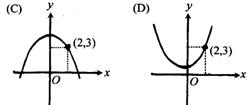
6．(03台湾)下列有关机率的叙述，何者正确? ( )
(A)投掷一枚图钉，针尖朝上、朝下的概率一样
(B)投掷一枚公正硬币，正面朝上的概率是
(C)统一发票有“中奖”与“不中奖”二种情形，所以中奖概率是
(D)投掷一粒均匀骰子，每一种点数出现的概率都是
，所以每投六次，必须出现一次“1点”
7． 把不等式组
的解集表示在数轴上，正确的是（ ）．
（A） （B） （C） （D）
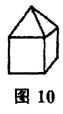
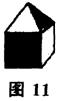
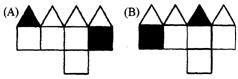
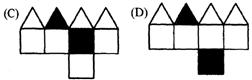
8. (03台湾)图1 O是由白色纸板拼成的立体图形，将此立体图形中的两面涂上颜色，如图11图10所示．下列四个图形中哪一个是图11的展开图? ( )
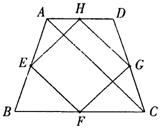
9．某花木场有一块等腰梯形ABCD的空地（如图），其各边的中点分别是点E、F、G、H，测量得对角线AC＝10米，现想用篱笆围成四边形EFGH场地，则需篱笆总长度是
A．40米
B．30米 C．20米
D．10米
10. 星期天晚饭后，小红从家里出去散步，下图描述了她散步过程中离家的距离s（米）与散步所用时间t（分）之间的函数关系．依据图象，下面描述符合小红散步情景的是（ ）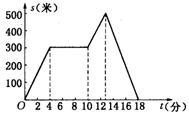
（A）从家出发，到了一个公共阅报栏，看了一会儿报，就回家了
（B）从家出发，到了一个公共阅报栏，看了一会儿报后，继续向前走了一段，然后回家了
（C）从家出发，一直散步（没有停留），然后回家了
（D）从家出发，散了一会儿步，就找同学去了，18分钟后才开始返回
二．填空题：（本大题共5小题，每小题3分，共15分
11、写出三个既是轴对称图形又是中心对称图形的图形 。
12．如图，点C、D在BE上，∠1＝∠2，BD＝EC，请补充一个条件：
，
使△ABC≌△FED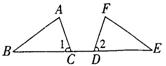
13．一年定期的存款，年息为1.98％，到期取款时需扣除利息的20％作为利息税上缴国库，假如某人存入一年的定期储蓄2000元，到期后可得本息和是 元。
14. 如图，点O是∠EPF的平分线上一点，⊙O和∠EPF的两边分别交于点A、B和C、D，根据上述条件，可以推出
．（要求：填写一个你认为正确的结论即可，不再标注其他字母，不写推理过程）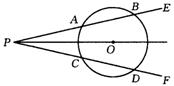
15．圆锥母线长5cm，底面半径长3cm，那么它的侧面展开图的圆心角是
三、解答下列各题：（每题6分，共30分）
16．计算：
17. 某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原售价的7折出售给一山区学校，结果每件盈利0.2元（盈利＝售价－进货价）．问该文具每件的进货价是多少元？
18．如图4，AB、AC分别是菱形ABCD的一条边和一条对角线，请用尺规把这个菱形补充完整．（保留作图痕迹，要求写作法）
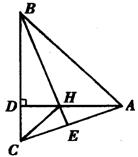
19．如图，△BDA、△HDC都是等腰直角三角形，且D在BC上，BH的延长线与 AC交于点E，请你在图中找出一对全等三角形，并写出证明过程．
20、反比例函数
的图象经过点A(2 ，3)，
⑴求这个函数的解析式；
⑵请判断点B(1 ，6)是否在这个反比例函数的图象上，并说明理由。
四．解答下列各题：（第21,22各8分，23,24题各9分，共34分）
21．某班有若干名学生参加数学竞赛，现将其成绩（得分均为整数）进行整理分成四个小组，并且列出频率分布表和作出部分频率分布直方图如下：
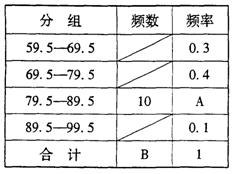
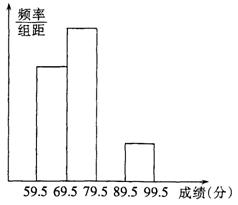
请你根据上表和上图，解答下列问题：
（1）从上表中可知，第三小组的频率A＝
.（2分）
该班参赛的学生人数B＝
人．（3分）
（2） 在上图中补全这个频率分布直方图．（3分）
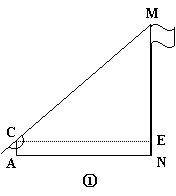
22．在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案（如图①所示）：
(1)在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=
;
(3)量出测倾器的高度AC=
.
根据上述测量数据，即可求出旗杆的高度MN.
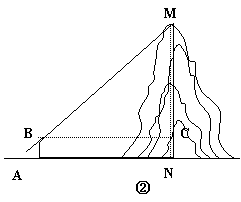
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图②）的方案：
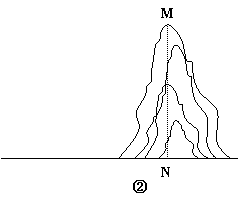(1)在图②中，画出你测量小山高度MN的示意图（标上适当字母）；
(2)写出你设计的方案.
 |
23、如图，△ABC中，AB=AC，过BC上一点D作BC的垂线，交BA延长线与P，交AC于Q。（1）判断△APQ的形状，并证明你的结论；
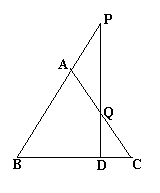（2）若∠B=60°，AB=AC=2，设CD=x，四边形ABDQ的面积为y，求y与x之间的函数关系式，并写出x的取值范围。
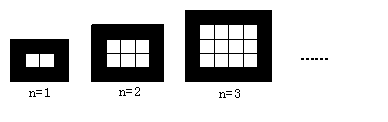
24．如图，用同样规格黑白两色的正方形瓷砖铺设地面，请观察图形并解答有关问题：
（1）在第n个图形中，需用白瓷砖、黑瓷砖各多少块？
（均用含n的代数式表示）
（2）按上述的铺设方案，设铺一块这样的矩形地面共用506块瓷砖，且黑瓷砖每块4元，白瓷砖每块3元，问一共需花多少元前购买瓷砖？
（3）是否存在黑白瓷砖块数相等的情形？请通过计算来说明？
五．解答下列各题：（第25题10分，26题11分）
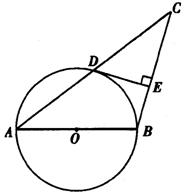
25．如图11，已知：AB是⊙O的直径，⊙O过AC的中点D，DE⊥BC，垂足为E．求证：①DE是⊙O的切线； ②
＝CE·CB．
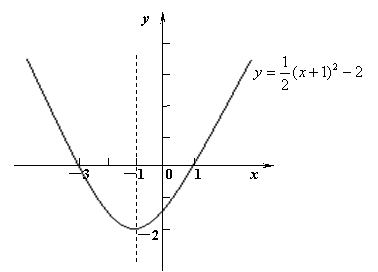
26．如图，抛物线
，
（1）设此抛物线与x轴交点为A、B（A在B的左边），请你求出A、B两点的坐标；
（2）有一条直线
，试利用图象法求出该直线与抛物线的交点坐标；
（3）P是抛物线上的一个动点，问是否存在一点P，使S△ABP=4,若存在,则有几个这样的点P,并写出它们的坐标.
参考答案：
一．1．A 2。A，3 B，4 D，5 A，6 B，7 C，8C，9C，10B
二．11，圆，正方形，菱形等
12，∠A＝∠F等
13， 2031.68
14，AB＝CD
15 216°
三．
16，解：原式＝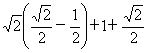
＝2
17．解：设该文具每件的进货价是x元
(x+2)×70%＝X＋0.2
X＝4（元）
答：设该文具每件的进货价是4元。
18．作法：（1）连接BC
（2）分别以点A，C为圆心，AB为半画弧，两弧交于点D，
（3）连接AD，CD
∴四边形ABCD为所求的菱形
19．解：△BDH≌△ADC
理由如下：∵△BDA和△HDC都是等腰直角三角形
∴BD＝DA，BDA＝ADC
DH＝DC
∴△BDH≌△ADC
20．解（1）反比例函数的图象经过点A(2 ，3
K＝6，
（2）点B(1 ，6)在这个反比例函数的图象上，理由如下：
∵当X＝1时，Y＝6
∴点B(1 ，6)在这个反比例函数的图象上
21．（1）0.2
（2）50
（3）
22．（1）如图：
（2）
(1)在测点A处安置测倾器，测得旗杆顶部M的仰角∠MBC=α;
(2)量出测点A到旗杆底部N的水平距离AN=;
(3)量出测倾器的高度AB=.
根据上述测量数据，即可求出旗杆的高度MN.
23．（1）△APQ为等腰三角形
理由如下：∵AB＝AC， ∴∠B＝∠C
又 ∠QDC＝90°
∴∠DQC＋∠C＝90°
∠P＋∠B＝90° ∴∠DQC＝∠P
又∵∠AQP＝∠DQC， ∠P＝∠AQP ∴AP＝AQ
（2）依题意可得：∵∠B＝60，AB＝AC＝2 ∴△ABC是等边三角形，S△ABC＝
过点A作AE⊥BC于点E，AE＝ ，
∵QD⊥BC ∴△CQD∽△CAE ∴
，∴QD＝X
S△QDC＝
Y＝S△ABC－S△QDC＝－ （0＜X＜1
24（1）n(n+1),, 4n+6
(2)∵n(n+1)+4n+6=506
∴n=20
∴20(20+1)×3+(4×20+6)×4=1604
（3）不存在
25．证明：（1）连接OD，DB
∵AB是直径，∴∠ADB＝90°
又∵△CDB≌△ADB
∴∠CBD＝∠ABD
∵OD＝OB
∠ABD＝∠ODB
∵DE⊥BC
∴∠CBD＋∠BDE＝90°
∴DE⊥OD
∴DE是为O的切线
（2）从（1）知，∠BDC＝90°，DE⊥BC，∴△CED∽△CDB ∴＝CE·CB
26（1）A（－3,0），B（1.0）
（2）交点坐标为（1,0）和（－1，－2）
（3）存在，P
P
P
P