中考数学真题演练4
一、选择题
1.(重庆市)如图,OA,BA分别表示甲、乙两名学生运动的一次函数图象,图中s和t分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快 ( )
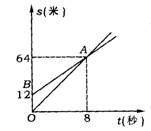
(A)2.5米 (B)2米 (C)1.5米 (D)1米
2.(沈阳市)两个物体A、B所受压强分别为PA(帕)与PB(帕)(PA、PB为常数),它们所受压力F(牛)与受力面积S(米2)的函数关系图象分别是射线lA、lB.如图所示,则 ( )
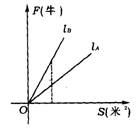
(A)PA<PB (B)PA=PB
(C)PA>PB (D)PA≤PB
3.(甘肃省)受力面积为S(米2)(S为常数,S≠0)的物体,所受的压强P(帕)压力F(牛)的函数关系为P=![]() ,则这个函数的图象是 ( )
,则这个函数的图象是 ( )
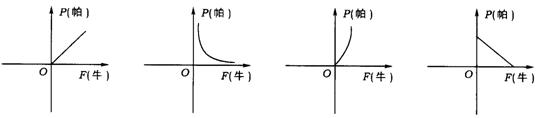
(A) (B) (C) (D)
4.(济南市)一游泳池长90米,甲、乙二人分别在游泳池相对两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,图中的实线和虚线分别为甲、乙与游泳池一边的距离随游泳时间的变化而变化图象.若不计转向时间,则从开始起到3分钟止他们相遇的次数为 ( )
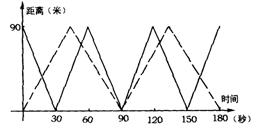
(A)2次 (B)3次 (C)4次 (D)5次
5.(吉林省)吉林省某大学的校门是一抛物线形水泥建筑物,大门的地面宽度为8米,两侧距离地面4米高处各有一个挂校名横匾的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计) ( )
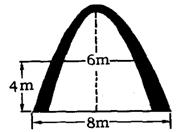
(A)9.2米 (B)9.1米 (C)9米 (D)5.1米
6.(安徽省)一段导线,在0℃时的电阻为2欧,温度每增加1℃,电阻增加0.008欧,那么电阻R欧表示为温度t℃的函数关系式为 ( )
(A)R=0.008t (B)R=2+0.008t
(C)R=2.008t (D)R=2t+0.008
7.(北京市西城区)如果一定值电阻R两端所加电压为5伏时,通过它的电流为1安,那么通过这一电阻电流I随它两端U变化的图象是 ( )
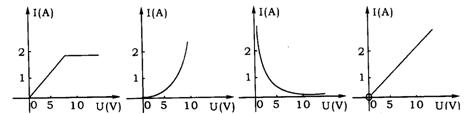
(A) (B) (C) (D)
8.(贵阳市)某天早晨,小强从家出发,以v1的速度前往学校,途中在一饮食店吃早点,之后以v2的速度向学校行进.已知v1>v2,下面的图象中表示小强从家到学校的时间t(分钟)与路程s(千米)之间的关系是 ( )
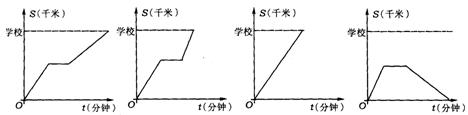
(A) (B) (C) (D)
9.(广东省)某装满水的水池按一定的速度放掉水池的一半水后,停止放水并立即按一定的速度注水,水池注满后,停止注水,又立即按一定的速度放完水池的水.若水池的存水量为v(立方米),放水或注水的时间为t(分钟),则v与t的关系的大致图象只能是 ( )
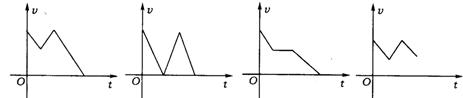
(A) (B) (C) (D)
10.(武汉市)某校举行趣味运动会,甲、乙两名学生同时从A地到B地,甲先骑自行车到B地后跑步回A地,乙则是先跑步到B地后骑自行车回A地(骑自行车速度快于跑步的速度),最后两人恰好同时回到A地.已知甲骑自行车比乙骑自行车的速度快.若学生离开A地的距离s与所用时间t的函数关系用图象表示如下(实线表示甲的图象,虚线表示乙的图象),则正确的是 ( )
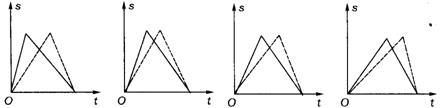
(A) (B) (C) (D)
11.(沈阳市)李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校.在课堂上,李老师请学生画出自行车行进路程x(千米)与行进时间t(小时)的函数图象的示意图,同学们画出的示意图如下,你认为正确的是 ( )
(A)① (B)② (C)③ (D)④
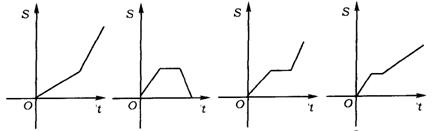
① ② ③ ④
12.(苏州市)如图,l甲、l乙分别是甲、乙两弹簧的长y(cm)与所挂物体质量x(kg)之间的函数关系的图象,设甲弹簧每挂1kg物体的伸长的长度为k甲cm,乙弹簧每挂1kg物体伸长的长度为k乙cm,则k甲与k乙的大小关系 ( )
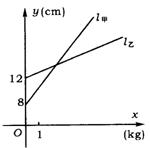
(A)k甲>k乙 (B)k甲=k乙
(C)k甲<k乙 (D)不能确定
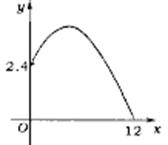
13.(武汉市)为了备战世界杯,中国足球队在某次训练中,一队员在距离球门13米处的挑射.正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-![]() ;②-
;②-![]() <a<0;③a-b+c>0;④0<b<-12 a.其中正确的结论是 ( )
<a<0;③a-b+c>0;④0<b<-12 a.其中正确的结论是 ( )
(A)①② (B)①④ (C)②③ (D)②④
二、填空题
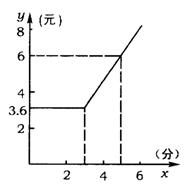
1.(长沙市)长沙向北京打长途电话,设通话时间x(分),需付电话费y(元).通话3分钟以内话费为3.6元,请你根据如图中y随x变化的图象,找出通话5分钟,需付电话费_______元.
三、解答题
1.(嘉兴、舟山、衢州)已知金属棒的长度l是温度t的一次函数,现有一根金属棒,在0℃时的长度是200cm,温度每升高1℃.它就伸长0.002cm
(1)求这根金属棒的长度l与温度t的函数关系式;
(2)当温度为100℃时,求这根金属棒的长度;
(3)当这根金属棒加热后长度伸长201.6cm时,求金属棒的温度.
2.(山西省)如图,公路上有A、B、C三站,一辆汽车在上午8时从离A站10千米的P地出发向C匀速前进,15分钟后离A站20千米.
![]()
(1)设出发x小时后,汽车离A站y千米,写出y与x之间的函数关系式;
(2)当汽车行驶到离A站150千米的B站时,接到通知要在中午12点超过B站30千米的C站,汽车若按原速能否按时到达?若能,是在几点几分到达;若不能,车速最少应提高到多少?
3.(南京市)声音在空气中传播的速度y(米/秒)(简称音速)是气温x(℃)的一次函数.下表列出了一组不同气温时的音速:
| 气温x(℃) | 0 | 5 | 10 | 15 | 20 |
| 音速y(米/秒) | 331 | 334 | 337 | 340 | 343 |
(1)求x与y之间的函数关系式;
(2)气温x=22(℃)时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放的烟花所在地约相距多远?
4.(海南省)我省某水果种植场今年喜获丰收,据估计,可收获荔枝和芒果共200吨.按合同,每吨荔枝售价为人民币0.3万元,每吨芒果售价为人民币0.5万元.现设销售这两种水果的总收入为人民币y万元,荔枝的产量为x吨(0<x<200).
(1)请写出y关于x的函数关系式;
(2)若估计芒果产量不小于荔枝和芒果总产量的20%,但不大于60%.请求出y值的范围.
5.(吉林省)一定质量的二氧化碳,当它的体积V=5m3时,它的密度r=19.8kg/m3.
(1)求出r与V的函数关系式;
(2)求当V=9m3时二氧化碳密度r.
6.(济南市)某风景区集体门票的收费标准是:20人以内(含20人),每人25元;超过20人,超过的部分,每人10元.
(1)写出应收门票费y(元)与游览人数x(人)(x≥20)之间的函数关系式;
(2)利用(1)中的函数关系式计算:某班54名学生去该风景区游览时,为购门票共花了多少元?
7.(广州市)某自行车保管站在某个星期日接受保管的自行车共有3500辆,其中变速车保管费是每辆一次0.5元,一般车保管费是每辆一次0.3元.
(1)若设一辆车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3500辆自行车中,变速车的辆次数小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.
8.(山东省)某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图所示.
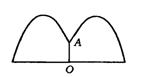
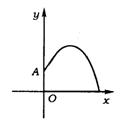
建立如图所示直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+x+![]() .
.
请回答下列问题:
(1)柱子OA的高度为多少米?
(2)喷出的水流距水平面最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
9.(河北省)某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).
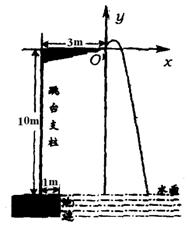
在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10![]() 米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边的距离为4米,同时,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3![]() 米,问此次跳水会不会失误?并通过计算说明理由.
米,问此次跳水会不会失误?并通过计算说明理由.
10.(吉林省)为了保护学生的视力,课桌椅的高度都是按一定的比例配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度:
| 第一套 | 第二套 | |
| 椅子高度x(cm) | 40.0 | 37.0 |
| 桌子高度y(cm) | 75.0 | 70.2 |
(1)请确定y与x的函数关系式(不要求写出x的取值范围);
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌,它们是否配套?请通过计算说明理由.
11.(南京市)在某一电路中,保持电压不变,电流I(安培)与电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培.
(1)求出I与R之间的函数关系式;
(2)当电流I=0.5安培时,求电阻R的值.
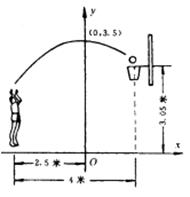
12.(吉林省)如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈,已知篮圈心到中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的解析式;
(2)该运动员身高1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?
注:抛物线y=ax2+bx+c的顶点坐标为(-![]() ,
,![]() ).
).
13.(安徽省)心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系:y=-0.1x2+2.6x+43(0≤x≤30).y值越大,表示接受能力越强.
(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐步降低?
(2)第10分时,学生的接受能力是多少?
(3)第几分时,学生的接受能力最强?
14.(沈阳市)随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势.试用你所学的函数知识解决下列问题:
(1)求入学儿童人数y(人)与年份x(年)的函数关系式;
(2)利用所求函数关系式,预测该地区从哪一年起入学儿童的人数不超过1000人?
| 年份(x) | 2000 | 2001 | 2002 | … |
| 入学和儿童人数(y) | 2520 | 2330 | 2140 | … |
15.(昆明市)某同学在做电学实验时,记录下电压y(伏特)与电流x(安培)有如下对应关系:
| x(安培) | … | 2 | 4 | 6 | 8 | 10 | … |
| y(伏特) | … | 15 | 12 | 9 | 6 | 3 | … |
请在平面直角坐标系中:
(1)通过描点连线,观察并求出y与x之间的函数关系式(不要求确定自变量x的取值范围);
(2)当电流是5安培时,电压是多少伏特?
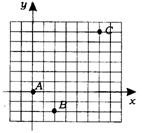
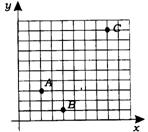
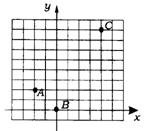
16.(广东省)在图的方格纸上有A、B、C三点(每个小方格的边长为1个单位长度).
(1)在给出的直角坐标系中(或舍去该直角坐标系,在自己另建立适当的直角坐标系中),分别写出点A、B、C的坐标;
(2)根据你得出的A、B、C三点的坐标,求图象经过这三点的二次函数的解析式.
参考答案
一、选择题
1.C 2.A 3.A 4.D 5.B 6.B 7.D 8.A 9.A 10.B 11.C 12.A 13.B
二、填空题
1.6
三、解答题
1.(1)金属棒的长度l与温度t的函数关系式是l=0.002t+200;
(2)当t=100℃时,t=0.002×100+200=200.2,
∴ 当温度为100℃时,这根金属棒的长度是200.2cm;
(3)由题意得201.6=0.002t+200,解得t=800.
∴ 当这根金属棒的长度伸长201.6cm时,金属棒的温度是800℃.
2.(1)汽车匀速前进的速度为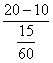 =40(千米/时)
=40(千米/时)
(2)当y=150+30=180时,40x+10=180,
解得x=4.25(小时),
8+4.25=12.25,因此汽车若按原速不能按时到达,
当y=150时,40x+10=150,解得x=3.5(小时)
设汽车按时到达C站,车速最少应提高到每小时v千米.
依题意得[(12-8)-3.5]v=30,∴ v=60(千米/时)
答:车速最少应提高到每小时60千米.
3.(1)设y=kx+b. ∵ x=0时,y=331;x=5时,y=334,∴ ![]()
∴ 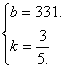 ∴ 所求函数关系式是y=
∴ 所求函数关系式是y=![]() x+331.
x+331.
(2)当x=22时,y=![]() ×22+331=344.2(米/秒).344.2×5=1721(米).
×22+331=344.2(米/秒).344.2×5=1721(米).
∴ 此人与燃放的烟花所在地约相距1721米
4.(1)因为荔枝为x吨,所以芒果为(200-x)吨,依题意,得
y=0.3x+0.5(200-x)=-0.2 x+100
即所求函数关系式为:y=-0.2 x+100(0<x<200=
(2)芒果产量最小值为200×20%=40(吨),此时,x=200-40=160(吨);最大值为:200×60%=120(吨),此时,x=200-120=80(吨).由函数关系式y=-0.2 ×80+100=84(万元).最小值为:y=-0.2×160+100=68(万元).∴ y值的范围为68万元≤y≤84万元.
5.(1)设二氧化碳质量为mkg
将V=5m3, r=19.8代入r=![]() ,得m=9.9(kg)
,得m=9.9(kg)
所求函数关系式为r=![]() .
.
(2)V=9代入r=![]() 得,r=1.1(kg/m3)
得,r=1.1(kg/m3)
6.(1)y=500+10(x-20)(x为整数,且x≥20).
(2)当x=54时,y=500+10(54-20)=840.
∴ 某班为购门票共花了840元.
7.(1)根据题意,得y=0.3x+0.5(3500-x).
y=-0.2x+1750.(x是正整数,0≤x≤3500)
(2)变速车停放的辆次不小于3500的25%,但不于3500的40%,也就是一般自行车停放辆次是在3500×60%与3500×75%之间.
当x=3500×60%=2100时,y=-0.2×2100+1750=1330;
当x=3500×75%=2625时,y=-0.2×3625+1750=1225.
这个星期日保管站保管费的收在1225元至1330元之间.
8.(1)抛物线y=-x2+x+![]() 与y轴交于A(0,
与y轴交于A(0,![]() ),
),
∴ 柱子OA的高度为12.5米.
(2)抛物线y=-x2+x+![]() 的顶点坐标是
的顶点坐标是![]() ,
,
∴ 喷出的水流距水平面的最大高度是2.25米.
(3)抛物线y=-x2+x+![]() 与x轴的两个交点是(
与x轴的两个交点是(![]() ,0),(-
,0),(-![]() ,0),而x≥0,
,0),而x≥0,
∴ x=-![]() 不合题意,舍去.
不合题意,舍去.
∴ 不计其他因素,水池的半径至少要2.5米,才能使喷出的水流不至于落在水池外.
9.(1)在给定的直角坐标系下,设最高点为A,入水点为B,
抛物线的解析式为:y=ax 2+bx+c
由题意知,O、B两点坐标依次为(0,0),(2,-10),且顶点A的纵坐标为![]() ,所以
,所以
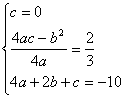
解得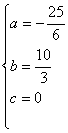 ,或
,或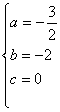 .
.
∵ 抛物线对称轴在y轴右侧,∴ -![]() >0,
>0,
又∵ 抛物线开口向下,∴ a<0,
∴ b>0,∴ a=-![]() ,b=
,b=![]() ,c=0
,c=0
∴ 抛物线的解析式为:y=-![]() x2+
x2+![]() x.
x.
(2)当运动员在空中距池边的水平距离为3![]() 米时,
米时,
即 x=3![]() -2=
-2=![]() 时,y=
时,y=![]() ×=-
×=-![]() .
.
∴ 此时运动员距水面的高为:10-![]() =
=![]() <5.
<5.
因此,此次试跳会出现失误.
10.(1)设y=kx+b,则有![]()
解得![]() ∴ y=1.6x=11.
∴ y=1.6x=11.
(2)当x=42.0时,y=1.6×42.0+11=78.2.
∴ 这套桌椅是配套的.
11.(1)设I=![]() .当R=5时,I=2,可得k=10,所以函数关系式为I=
.当R=5时,I=2,可得k=10,所以函数关系式为I=![]() ,
,
IR=10.
(2)当I=0.5时,可得R=20(欧姆).
12.(1)设所求抛物线y=ax 2+bx+c,顶点(0,3.5)和(1.5,3.05)在抛物线上
∴ 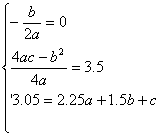 ,解得
,解得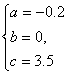
∴ y=-0.2x 2+3.5.
(2)当x=-2.5时.y=-0.2×(-2.5)2+3.5=2.25.
2.25-1.8-0.25=0.20(米).
答:球出手时,他距离地面高度为0.20米.
13.(1)y=-0.12+2.6x+43=-0.1(x-13)2+59.9.所以,当0≤x≤13时,学生的接受能力逐步增加.当0<x≤13时,学生的接受能力逐步下降.
(2)当x=10时,y=-0.1(10-13)2+59.9=59.第10分时,学生的接受能力为59.
(3)x=13时,y取得最大值,所以,在第13分时,学生的接受能力最强.
14.(1)解法一:设y=kx+b.由于直线 y=kx+b过(2000,2520),(2001,2300)两点,故有![]() 解得
解得![]() ∴ y=-190x+382520过点(2002,2140),所以y=-190x+382520较好地描述了这一变化趋势.故所求函数关系式为y=-190x+382520.
∴ y=-190x+382520过点(2002,2140),所以y=-190x+382520较好地描述了这一变化趋势.故所求函数关系式为y=-190x+382520.
解法二:设y=ax2+bx+c.由于y=ax2+bx+c过(2000,2520),(2001,2330),(2002,2140)三点,故有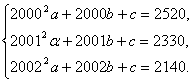 解得a=0,b=-190,c=382520.∴ y=-190x+382520.
解得a=0,b=-190,c=382520.∴ y=-190x+382520.
因为y=-190x+382520过(2000,2520),(2001,2330),(2002,2140)三点,所以y=-190x+382520较好的描述了这一变化趋势.故所求函数关系式为y=-190x+382520.
(2)设x年时,入学人数为1000人.由题意得:-190x+382520=1000,解得:x=2008.
答:从2008年起入学儿童的人数不超过1000人.
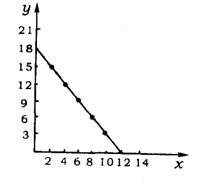
15.(1)描点连线,画出如图,发现:y与x之间的函数关系式为y=kx+b.代入5个已知点中的任意两个列出方程组如![]() 求出解析式为y=-1.5x+18.
求出解析式为y=-1.5x+18.
(2)当x=5时,y=-1.5×5+18=10.5
16解法一(在所给的直角坐标系中计算)
(1)点A的坐标是(2,3),点B的坐标是(4,1),点C的坐标是(8,9).
(2)设所求的二次函数解析式为y=ax2+bx+c.
把点A、B、C的坐标分别代入上式,得:
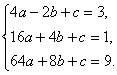 解之,得
解之,得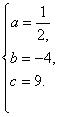
∴ 所求的二次函数的解析式为y=![]() x2-4x+9.
x2-4x+9.
解法二(在以B为原点,另建的直角坐标系中计算)
(1)以B为原点,建立如图所示的直角坐系.
点A的坐标是(-2,2),点B的坐标是(0,0),点C的坐标是(4,8).
(2)设所求的二次函数解析式为:y=ax2+bx+c,把点A、B、C的坐标分别代入上式,得: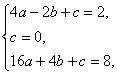 解得,得
解得,得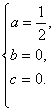 ∴ 所求的二次函数的解析式为y=
∴ 所求的二次函数的解析式为y=![]() x2.
x2.
解法三(在以点A为原点,另建的直角坐标系中计算)
(1)以A为原点,建立如图所示的直角坐标系.点A的坐标是(0,0).点B的坐标是(2,-2),点C的坐标是(6,6).
(2)设所求的二次函数解析式为y=ax2+bx+c,
把点A、B、C的坐标分别代入上式,得:
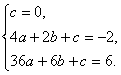 解之,得
解之,得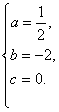 ∴ 所求的二次函数的解析式为y=
∴ 所求的二次函数的解析式为y=![]() x2-2x.
x2-2x.