中考数学真题演练5 一、选择题
1．（江西省）如图，PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中，错误的是 （ ）
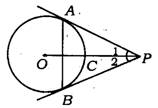
（A）∠1＝∠2 （B）PA＝PB
（C）AB⊥OP （D）P
＝PC·PO
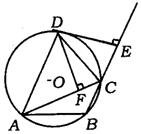
2．（苏州市）如图，⊙O的内接△ABC外角∠ACE的平分线交⊙O于点D．DF⊥AC，垂足为F，DE⊥BC，垂足为E．给出下列几个结论：①CE＝CF；②∠ACB＝∠EDF；③DE是⊙O的切线；④
＝
．其中一定成立的是 （ ）
（A）①②③ （B）②③④
（C）①③④ （D）①②④
3．（海南省）已知AB、CD是⊙O的两条直径，则四边形ADBC一定是 （ ）
（A）等腰梯形 （B）正方形
（C）菱形 （D）矩形
二、填空题
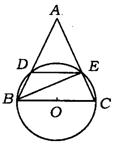
1．（新疆乌鲁木齐）如图，已知等腰△ABC中，∠A＝
，底边BC为⊙O的直径，两腰AB、AC分别与⊙O交于点D、E．有下列序号为①~④的四个结论：①AD＝AE；②DE∥BC，③∠A＝∠CBE；④BE⊥AC．其中结论正确的序号是_________．
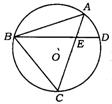
2．（昆明市）如图，已知：⊙O的弦AC、BD相交于点E，点A为
上一动点，当点A的位置在________时，△ABE∽△ACB．
三、解答题：
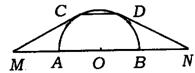
1．（上海市）已知：如图，AB是半圆O的直径，弦CD∥AB，直线CM、DN分别切半圆于点C、D，且分别和直线AB相交于点M、N．
（1）求证：MO＝NO；
（2）设∠M＝
，求证：MN＝4CD．
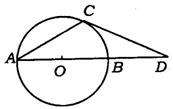
2．（甘肃省）如图，AB是⊙O的直径，点D在AB的延长线上，且BD＝OB，点C在⊙O上，∠CAB＝．求证：DC是⊙O的切线．
3．（山东省）如图，已知等腰直角三形ABC中，∠CAB＝
，AD⊥BC，垂足为D，⊙O过A、D两点，分别交AB、AC、BD于E、F、G（G在D的左侧）．
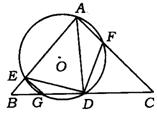
（1）求证：EG＝AF．
（2）若AB＝
，⊙O的半径为
，求tan∠ADE的值．
4．（杭州市）如图，⊙O1与⊙O2外切于点C，⊙O1与⊙O2的连心线与外公线相交于P，外公切线与两圆的切点分别为A、B，且AC＝4，BC＝5．
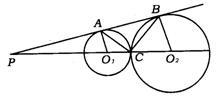
（1）求线段AB的长；
（2）证明：
5．（河南省）已知：如图，△ABC内接于⊙O1，AB＝AC，⊙O2与BC相切于点B，与AB相交于点E，与⊙O1相交于点D，直线AD交⊙O2于点F，交CB的延长线于G．求证：
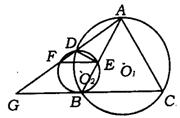
（1）∠G＝∠AFE；
（2）AB·EB＝DE·AG．
6．（贵阳市）已知：如图，圆内接四边形ABCD的一组对边AB、DC的延长线相交于点E．且∠DBA＝∠EBC．求证：AD·BE＝EC·BD．
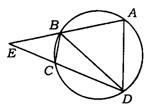
7．（新疆乌鲁木齐）如图，已知⊙O的两条弦AC、BD相交于点Q，OA⊥BD．
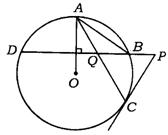
（1）求证：
＝AQ·AC；
（2）若过点C的⊙O的切线交DB的延长线于点P，求证：PC＝PQ．
8．（成都市）已知：如图，⊙O的半径为R，CD是⊙O的直径，以点D为圆心，以r（r＜R）为半径作圆D，⊙D与⊙O相交于A、B两点，BC的延长线与⊙D相交于点E，连结AE．
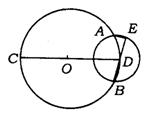
求证：（1）AE∥CD；（2）AE＝
9．（扬州市）已知：如图，AB是⊙O的直径，CD⊥AB，垂足为D，CE切⊙O于点F，交AB的延长线于点E．求证：EF·EC＝EO·ED．
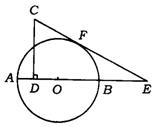
10．（常州市）如图，四边形ABCD内接于⊙O，边AD、BC的延长线相交于点P，直线AE切⊙O于点A，且AB·CD＝AD·PC．
求证：（1）△ABD∽△CPD；（2）AE∥BP
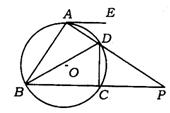
11．（武汉市）已知：如图，在⊙O中，AB为弦，C、D两点在AB上，且AC＝BD．求证：△OCD为等腰三角形．
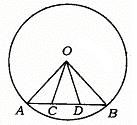
12．（西宁市）如图，⊙O是以Rt△ABC的直角边AC为直径的圆，且与斜边AB相交于点D，过D作DH⊥AC，垂足为H，又过D作直线交BC于E，使∠HDE＝2∠A．
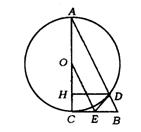
求证：（1）DE是⊙O的切线；
（2）OE是Rt△ABC的中位线．
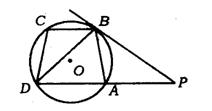
13．（乌鲁木齐市）已知如图，四边形ABCD内接于⊙O，BC∥AD，PB切⊙O于B．交DA的延长线于P点，求证：AP·BD＝BP·CD．
14．（北京市顺义区）已知：如图，四边形ABCD内接于⊙O，AB为直径，过点C的切线交AD的延长线于点E，且AE⊥EC．
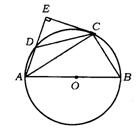
求证：（1）DC＝BC；
（2）若DC︰AB＝3︰5，求∠ACD的正弦值．
15．（天津市）已知，如图，两圆内切于点P，大圆的弦AB切小圆于点C，PC的延长线交大圆于点D．
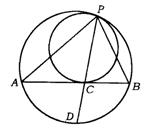
求证：（1）∠APD＝∠BPD；
（2）PA·PB＝PC2＋PA·CB．
16．（辽宁省）已知：如图，△ABC内接于⊙O1，AB＝AC，⊙O2与BC相切于点B，与AB相交于点E，与⊙O1相交于点D，直线AD交⊙O2于点F，交CB的延长线于点G．
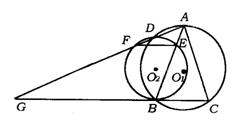
求证：（1）EF∥CG；
（2）AB·EB＝DE·AG．
17．（哈尔滨市）已知：如图，BD是⊙O的直径，弦AC⊥BD，垂足为E，BA和CD的延长线交于点P．
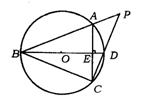
求证：（1）AB＝BC；
（2）CD·PC＝PA·PB．
18．（甘肃省）如图，在内切的两圆中，设C为小圆的圆心，O为大圆的圆心，P为切点，⊙O的弦PQ和⊙C相交于R，过点R作⊙C的切线与⊙O交于点A、B．
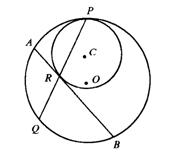
求证：Q是
的中点．
19．（镇江市）已知：如图，⊙O1和⊙O2内切于点T，⊙O2的弦CD切⊙O1于点E，连结TC、TD分别交⊙O1于A、B，TE的延长线交⊙O2于点F，连结AB、FD．
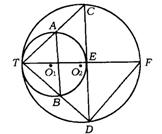
求证：（1）AB∥CD；
（2）∠CTF＝∠DTF；
（3）DF2－EF2＝CE·DE．
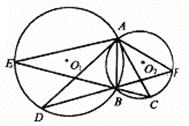
20．（武汉市）如图，⊙O1与⊙O2相交于A、B两点，AC是⊙O1的切线且交⊙O2于点C，AD是⊙O1的切线且交⊙O1于点D，连结DB、CB、AB．
21．（广州市）如图，设点D、E分别为△ABC的外接圆、
的中点，弦DE交AB于点F，交AC于点G．
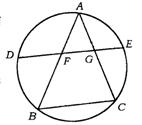
求证：AF·AG＝DF·EG．
22．（成都市）已知，如图，在△ABC中，AB＝AC，过点A的直线与△ABC外接圆O交于点D，与BC的延长线交于点F，DE是BD的延长线，连结CD．
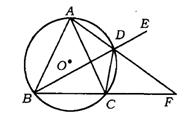
求证：（1）FF平分∠EDC；
（2）AF2－AB2＝AF·DF．
23．（成都市）已知：如图，⊙O1和⊙O2外切于A，BC是⊙O1和⊙O2的公切线，切点为B、C，连结BA并延长交⊙O1于D，过D点作CB的平行线交⊙O2于E、F．
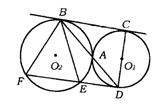
求证：（1）CD是⊙O1的直径；
（2）试判断线段BC、BE、BF的大小关系，并证明你的结论．
24．（贵阳市）已知：如图所示，AB为⊙O的直径，BD是⊙O的切线，B为切点，劣弧
＝
．连结AE并延长交BD于D，连结AC．
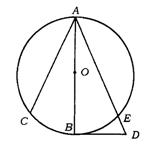
求证：AB2＝AC·AD．
25．（贵阳市）如图，△ABC内接于⊙O，∠BAC的平分线交BC于D．交⊙O于E，EF∥BC交AC的延长线于F，连结CE．
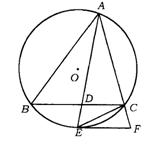
求证：（1）∠BAE＝∠CEF；
（2）EF是⊙O的切线．
参考答案
一、选择题
1．D 2．D 3．D
二、填空题
1．①②④ 2．
的中点
三、解答题：
1．连结OC、OD．
（1）∵ OC＝OD，∴∠OCD＝∠ODC．∵CD∥AB，∠OCD＝∠DOM，∠ODC＝∠DON．
∴ ∠COM＝∠DON．∵CM、DN分别切半圆O于点C、D，∴∠OCM＝∠ODN＝．
∴ △OCM≌△ODN．∴OM＝ON．
（2）由（1）△OCM≌△ODN可得∠M＝∠N．∵∠M＝，∠N＝．
∴ OM＝2OC，ON＝2OD，∠COM＝∠DON＝
∴∠COD＝．
∴ △OCD是等边三角形，即CD＝OC＝OD．∴MN＝OM＋ON＝2OC＋2OD＝4CD．
2．连结OC、BC，∵AB为⊙O的直径，∴∠ACB＝．
又∵ ∠CAB＝，∠ABC＝．
∵ OB＝OC，∴△BOC为等边三角形．
∴ BC＝OB＝BD，即△BCD为等腰三角形．
又 ∠CBD＝
，∴∠BCD＝．
∴ ∠OCD＝∠OCB＋∠BCD＝＋＝，
点C在⊙O上，故DC是⊙O的切线．
3．（1）在圆内接四边形形AEDF中，∵∠EAF＝，∴∠EDF＝（圆内接四边形对角互补），即∠ADF＋∠EDA＝．又∠GDE＋∠EDA＝，∴∠GDE＝∠ADF，
∴
，∴EG＝AF．
（2）在圆内接四边形AEGD中，∵∠ADG＝，∴∠AEG＝．又∵△ABC是等腰直角三角形，∴△BEG是等腰直角三角形．边结AG，则AG是⊙O的直径，∴AG＝
．
在Rt△BEG中，设EG＝x，BE＝x，AE＝
，由勾股定理，
，即
，解得
或x＝1．当时，BG＝2，而BD＝
＜2，不符合图中实际，舍去．∴tan∠ADE＝tan∠AGE 
．
4．（1）由已知条件可得∠A
，又
（∠A
），所以∠ACB＝，AB＝
．
（2）由已知条件解（1）过程中的有关结论，可知∠AC
与∠ABC都是∠BC
（∠BC＝∠CB）的余角，在△PAC与△PCB中，∠P＝∠P，∠PCA＝∠PBC，所以△PCA∽△PBC．有
，即证得．
5．（1）连结BD．∵∠FEB＝∠FDB，∠FDB＝∠C．∴∠FEB＝∠C．
又∵AB＝AC，∴∠ABC＝∠C．∴∠FEB＝∠ABC．∴EF∥CG，∴∠G＝∠AFE．
（2）连结BF．∵∠ADE＝∠ABF，∠DAE＝∠BAF．∴△ADE∽△ABF，∴
．∵EF∥CG，∴
，∴
．∴．∵∠BEF＝∠ABC，∠ABC＝∠BFE，∴∠BEF＝∠BFE，∴BE＝BF．∴
．∴ AB·EB＝DE·AG．
6．∵ 四边形ABCD是圆内接四边形，∴ ∠BCE＝∠A，又∵ ∠DBA＝∠EBC，∴ △ABD∽△CBE，∴ 
．∴ AD·BE＝EC·BD．
7．（1）连结BC．∵ OA⊥BD，∴ 由垂径定理知
，在△ABQ与△ACB中，∵ ∠BAQ＝∠CAB，由
∠ABQ＝∠ACB．于是△ABQ∽ACB．则
．故AB
＝AQ·AC．
（2）连结OC，∵ OA＝OC，∴ ∠ACO＝∠CAO，又PC是⊙O的切线，∴ OC⊥PC，即∠ACO＋∠PCQ＝，由已知OA⊥BD知∠CAO＋∠AQD＝．又∵ ∠CAO＝∠AQD．
∠CAO＋∠PQC＝．于是有∠PCQ＝∠PQC．故PC＝PQ．
8．（1）连结AB，则CD⊥AB．又∵ BE是⊙D的直径，∴ ∠EAB＝，即AE⊥AB．∴ AE∥CD．
（2）连结CB，则∠CBD＝．CD⊥AB，∴ 
．∴ ∠C＝∠EBA．∴ Rt△CDB∽Rt△BEA．∴ 
，即
．∴ 
．
9．连结OF，∵ CE切⊙O于点F，∴ OF⊥CE，∵ CD⊥AB，∴ ∠CDE＝∠OFE＝又∵ ∠E＝∠E，∴ △CDE∽△OFE，∴ 
，∴ EF·EC＝EO·ED．
10．
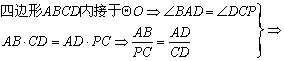△ABD∽△CPD∠ABD＝∠P
AE∥BP．
11．∵ OA＝OB，∠A＝∠A，AC＝BD．
∴ △AOC≌△BOD．∴ OC＝OD．∴ △OCD为等腰三角形．
12．（1）连结OD，则OD是⊙O的半径，
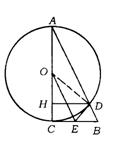
∵ ∠HDE＝2∠A，∠DOH＝2∠A，
∴ ∠HDE＝∠DOH，
又 DH⊥AC，
∴ ∠DOH＋∠ODH＝90°，
∴ ∠HDE＋∠ODH＝90°，
∴ DE是⊙O的切线．
（2）∵ DE是⊙O的切线，
∴ ∠ODE＝90°，又OC＝OD，OE＝OE，
∴ △ODE＝≌△OCE，∴ ∠COE＝∠DOE，
又 ∠A＝
∠COD，∴ ∠COE＝∠A，∴ OE∥AB，
又 AO＝OC，∴ OE是△ABC的中位线．
13．∵ 四边形ABCD内接于⊙O，∴ ∠C＝∠BAP
又 ∵ PB切⊙O于B，∴ ∠PBA＝∠BDA．
又 ∵ CB∥DA，∴ ∠BDA＝∠DBC．
即 ∠DBC＝∠PBA，∴ △CBD∽△ABP，
∴ 
即 AP·BD＝BP·CD．
14．（1）证法一：如图，
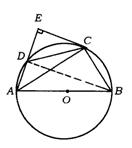
∵ AB是⊙O的直径，
∴ ∠ACB＝90°，
∵ AE⊥EC，
∴ ∠AEC＝90°，
∴ ∠AEC＝∠ACB．
∵ EC是⊙O的切线，
∴ ∠ECA＝∠CBA，
∴ △ACE∽△ABC，
∴ ∠EAC＝∠CAB．
∴ 
＝，
∴ DC＝BC．
证法二：如图，连结BD、OC相交于点F，
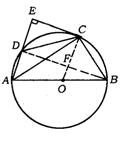
∵ AB是⊙O的直径，
∴ ∠ADB＝90，
∵ EC是⊙O的切线，
∴ ∠ECF＝90°
∵ AE⊥EC，
∴ ∠DEC＝90°，
∴ 四边形CEDF是矩形．
∴ OC⊥BD，FC＝DE，
∴ ＝，
∴ DC＝BC．
（2）解法一：设DC＝3a，则BC＝3a，AB＝5a，
在Rt△ABC中，由勾股定理，得AC＝
＝4a．
∵ △ACE∽△ABC，∴ 
∴ 
，∴ EC＝
a，AE＝
a．
在Rt△DEC中，由勾股定理，得DE＝
＝
a．
∵ AD＝AE－DE，∴ AD＝a－a＝
a．
连结BD，则∠ADB＝90°，∠ACD＝∠ABD．
∴ sin∠ACD＝sin∠ABD＝
＝
．
解法二：DC＝3a，则BC＝3a，AB＝5a，
∵ AB是⊙O的直径，∴ ∠ACB＝90°．
∴ ∠CED＝∠ACB，∠EDC＝∠CBA，∴ △DEC∽△BCA．
∴ 
，∴ 
，∴ DE＝a．
∴ FC＝a，∴ OF＝OC－FC＝
a－a＝
a，
∵ ∠ACD＝∠ABD．
∴ sin∠ACD＝sin∠OBF＝
＝．
15．（1）如图，过P作两圆的公切线MN，
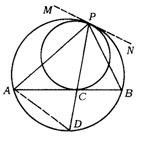
∵ MN与AB均为小圆切线，且弦切角∠NPC与∠BCP所夹的弧均为
．
∴ ∠NPC＝∠BCP．
∵ ∠NPC＝∠NPB＋∠BPC，
∠BCP＝∠PAC＋∠APC，
而 ∠NPB＝∠PAB＝∠PAC，
∴ ∠NPC－∠BCP＝∠NPB＋∠BPC－∠PAC－∠APC，
∴ ∠BPC＝∠APC，即 ∠BPD＝∠APC．
（2）连结AD．
在△PDA和△PBD中，由（1）可知∠DPA＝∠BPC．
又∵ ∠ADP＝∠CBP，∴ △PDA∽△PBC．
∴ 
，即 PA·PB＝PD·PC，
∵ PD·PC＝（PC＋CD）·PC＝PC2＋PC·PD．
又∵ PC·PD＝AC·BC，∴ PC·PD＝PC2＋AC·BC．
∴ PA·PB＝PC2＋AC·BC．
16．如图，
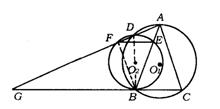
（1）证法一：连结BD，
∵ ∠FEB＝∠FDB，∠FDB＝∠C，
∴ ∠FEB＝∠C，
又∵ AB＝AC，
∴ ∠ABC＝∠C，
∴ ∠FEB＝∠ABC，∴ EF∥CG．
证法二：也可证出∠AGB＝∠EFD（同位角），
得出EF∥CG．
（2）证法一：连结DE，∴ EF∥CG，∴ ∠DFE＝∠G，
又∵ ∠DBE＝∠DFE，∴ ∠DBE＝∠G，
即 ∠DBE＝∠CGA，
∵ ∠ABC＝∠C，∠ABC＝∠BDE，
∴ ∠BDE＝∠C， 即 ∠BDE＝∠GCA．
∴ △BDE∽△GCA．∴ 
．
∵ AB＝AC，∴ AB·EB＝DE·AG．
证法二：连结BF，可证△ADE∽△ABF，得
．
由EF∥CG，得
，从而可得，
再证BE＝BF．得AB·EB＝DE·AG．
17．连结AD，如图，
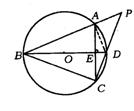
（1）∵ BD是直径，AC⊥BD，
∴ ＝，
＝，
∴ AB＝BC，AD＝DC．，
（2）∵ 四边形ABCD内接于⊙O，
∴ ∠PDA＝∠PBC，
又∵ ∠P＝∠P，∴ △PAD∽△PCB．∴ 
，
∴ PA·CB＝AD·PC，
∵ AB＝BC，AD＝DC，∴ CD·PC＝PA·AB．
18．如图连结PC并延长，由连心线性质可知O一定在PC的延长线上，连结CR，OQ．
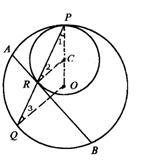
∵ AB切小圆于R，∴ CF⊥AB．
又 ∵ CP＝CR，∴ ∠1＝∠2
同理 OP＝OQ，得 ∠1＝∠3．
∴ ∠2＝∠3．∴ CR∥OQ，
∴ OQ⊥AB，
∴ Q是的中点（垂径定理）．
19．（1）过点T作两圆的公切线TP，
∵ ∠PTD＝∠TAB，∠PTD＝∠TCD，
∴ ∠TAB＝∠TCD，∴AB∥CD
（2）方法一：连结AE，
∵ EC是⊙O1的切线，∴ ∠CEA＝∠CTF．
∵ AB∥CD，∴ ∠CEA＝∠EAB．
又∵ ∠EAB＝∠DTF，∴ ∠CTF＝∠DTF．
方法二：∵ TP、CD是⊙O1的切线．
∴ ∠PTE＝∠DET．
∵ ∠DET＝∠C＋∠CTE，∠PTE＝∠PTD＋∠DTF，∠PTD＝∠C，
∴ ∠CTF＝∠DTF．
方法二：连结O1E．∵ CD切⊙O1于点E，∴ O1E⊥CD．
∵ AB∥CD，∴ O1E⊥AB，∴ 
＝，
∴ ∠CTF＝∠DTF．
（3）∵ ∠CDF＝CTF，∠∠CTF＝∠DTF．∴ ∠CDF＝∠DTF．
又∵ ∠DFE＝∠TFD，∴ △DFE∽△TFD．
∴ 
，即 DF2＝EF·TF．
∵ TF＝TE＋EF，
∴ DF2＝EF·（TE＋EF）＝EF·TE＝EF2，
∴ DF2－EF2＝EF·TE．
∵ EF·TE＝CE·DE，∴ DF2－EF2＝CE·DE．
20．（1）AC为⊙O1的切线，
∴ ∠BAC＝∠D，同理∠DAB＝∠C，
∴ 
，
即 AB2＝BC·BD．
（2）如图，连结ED，则∠ADE＝∠ABE＝∠BAC＋∠C，
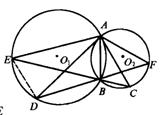
∠AED＝∠ABF＝∠BAD＋∠ADB．
由（1）知△ABC∽△DBA，
∴ ∠BAC＋∠C＝∠BAD＋∠ADB，
∴ ∠ADE＝∠AED，
∴ AE＝AD．
而 ∠AEB＝∠ADB，∠C＝∠F，
∴ △AEC≌△ADF．
21．如图，连结AD、AE，
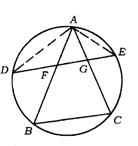
∵ D是的中点，
∴ ＝
．∴ ∠BAD＝∠AED．
同理可证∠ADE＝∠CAE．
∴ △ADF∽△EAG．
∴ 
，∴ AF·AG＝DF·EG．
22．（1）∵ AB＝AC，∴ ∠ABC＝∠ACB．
∵ ∠ADB＝∠ACB，∠ADB＝∠FDE，
∴ ∠FDE＝∠ACB＝∠ABC，
∵ ∠CDF＝∠ABC，
∴ ∠CDF＝∠FDE，即DE平分∠EDG．
（2）在△ADF和△ADC中，
∵ ∠CDF＝∠ABC＝∠ACB，∴ ∠ACF＝∠ADC．
∵ ∠CAF＝∠DAC，∴ △ACF∽△ADC．
∴ 
，即 AC2＝AD·AF．
∵ AB＝AC，∴ AB2＝AD·AF．
∴ AF2－AB2＝AF2－AD·AF＝AF（AF－AD）＝AF·DF．
23．（1）如图，过点A作⊙O1和⊙O2的内公切线交BC于点G，连结AC．
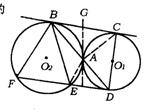
∵ GB、GA分别切⊙O2于B、A，
∴ GB＝GA，同理 GC＝GA．
∴ GA＝GB＝GC．
∴ AB⊥AC，即∠CAD为直角，
∴ CD是⊙O1的直径．
（2）结论是BC＝BE＝BF．连结AE．
在△ABE和△EBD中，∵ ∠CBA＝∠BEA，
又∵ BC∥FD，∴ ∠CBA＝∠BDE．
∴ ∠BEA＝∠BDE．
又∵ ∠ABE＝∠EBD，∴ △ABE∽△EBD．
∴ 
，即BE2＝BA·BO．
∵ ∠CBE＝∠BFE，
又∵ BC∥FD，∴ ∠CBE＝∠BEF，
∴ ∠BFE＝∠FEB，∴ BE＝BF．
∴ BE＝BF＝BC．
24．证明：连结BC．
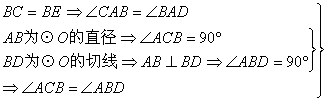
△ABC∽△ADBÞ
ÞAB2＝AD·AC．
25．（1）证明：
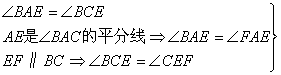
Þ∠BAE＝∠CEF
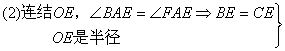
Þ
ÞOE⊥EFÞEF是⊙O的切线．