中考数学真题演练7
一、选择题
1.(山西省)如图,BC是⊙A的内接正十边形的一边,BD平分∠ABC交AC于点D,则下列结论不成立的是 ( )
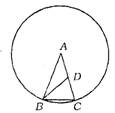
(A)BC=BD=AD
(B)BC2=DC·AC
(C)△ABC三边之比为1∶1∶![]()
(D)BC=![]() AC
AC
2.(哈尔滨市)下列命题中,错误的是 ( )
(A)对角线互相平分且垂直的四边形是菱形
(B)直角梯形既不是轴对称图形,也不是中心对称图形
(C)对角线互相平分且相等的四边形是矩形
(D)平分弦的直径必垂直于弦
3.(长沙市)下列命题正确的是 ( )
(A)对角线相等的四边形是矩形
(B)相邻的两个角都互补的四边形是平行四边形
(C)平分弦的直径垂直于弦,并且平分弦所对的两条弧
(D)三点确定一个圆
4.(四川省)下列命题中,真命题是 ( )
(A)等腰梯形是中心对称图形
(B)对角线相等且互相垂直的四边形是菱形
(C)相等的圆心角所对的弦相等
(D)相似三角形周长的比等于对应中线的比
5.(天津市)有如下四个结论:
①有两边及一角对应相等的两个三角形全等:
②菱形既是轴对称图形,又是中心对称图形;
③平分弦的直径垂直于弦,并且平分弦所对的两条弧;
④两圆的公切线最多有4条.
其中正确结论的个数为 ( )
(A)1个 (B)2个 (C)3个 (D)4个
6.(武汉市)已知:以定线段AB为直径作半圆O,P为半圆上任意一点(异于A、B),过点P作半圆O的切线分别交过A、B两点的切线于D、C,AC、BD相交于N点,连结ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP·PC为定值;④PA为∠NPD的平分线,其中一定成立的是 ( )
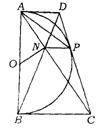
(A)①②③ (B)②③④ (C)①③④ (D)①④
二、填空题
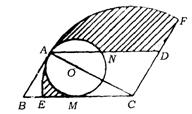
1.(武汉市)已知:如图□ABCD中,AC⊥CD,以C为圆心,CA为半径作圆弧交BC于E,交CD的延长线于点F,以AC上一点O为圆心OA为半径的圆与BC相切于点M,交AD于点N.若AC=6厘米,OA=2厘米,则图中阴影部分的面积为________平方厘米.
三、解答题:
1.(北京市东城区)已知,如图,P是⊙O直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E.
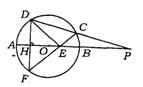
(1)求证:PA·PB=PO·PE;
(2)若DE⊥CF,∠P=15°,⊙O的直径为2,求弦CF的长.
2.(北京市海淀区)如图,AB是⊙O的直径,AE平分∠BAF交⊙O于点E,过点E作直线与AF垂直交AF延长线于D点,且交AB延长线于C点.
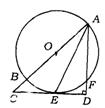
(1)求证:CD与⊙O相切于点E;
(2)若CE·DE=![]() .AD=3,求⊙O的直径及∠AED的正切值.
.AD=3,求⊙O的直径及∠AED的正切值.
3.(山西省)已知:如图,A是⊙O1、⊙O2的一个交点,点M是O1O2的中点,过点A的直线BC垂直于MA.分别交⊙O1、⊙O2于B、C.
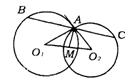
(1)求证:AB=AC;
(2)若O1A切⊙O2于点A,弦AB、AC的弦心距分别为d1、d2,求证:d1+d2=O1O2;
(3)在(2)的条件下,若d1d2=1,设⊙O1、⊙O2的半径分别为R、r,求证:R2+r2=R2r2.
4.(哈尔滨市)如图,⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的外公切线,B、C为切点.AT为内公切线,AT与BC相交于点T.延长BA、CA,分别与两圆交于点E、F.
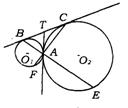
(1)求证:AB·AC=AE·AF;
(2)若AT=2,⊙O1与⊙O2的半径之比是1∶3,求AE的长.
5.(宁夏回族自治区)用两种方法解答
如图,矩形ABCD外切于半圆,AD与半圆相切于F,BC是半圆的直径,O为圆心,且BC=10厘米,对角线AC交半圆于P,PE⊥BC于E.求P到BC的距离.
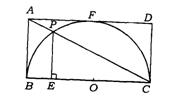
6.(南京市)已知:如图,⊙O1与⊙O2相交于A、B两点,O1在⊙O2上,⊙O2的弦BC切⊙O1于B,延长BO1、CA交于点P,PB与⊙O1交于点D.
(1)求证:AC是⊙O1的切线;
(2)连结AD、O1C.求证:AD∥O1C;
(3)如果PD=1,⊙O1的半径为2,求BC的长.
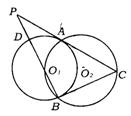
7.(长沙市)如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足E,且PC2=PE·PO.
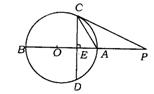
(1)求证:PC是⊙O的切线.
(2)若OE∶EA=1∶2,PA=6,求⊙O的半径.
(3)求sin∠PCA的值.
8.(贵阳市)已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD·AE=2![]() .
.
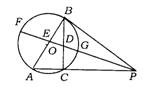
(1)求证:△BPD∽△APE;
(2)求FE·EG的值;
(3)求tan∠BDE的值.
9.(扬州市)如图,破残的圆形轮片上,弦AB的垂直平分线交![]() 于点C,交弦AB于点D.已知:AB=24厘米,CD=8厘米.
于点C,交弦AB于点D.已知:AB=24厘米,CD=8厘米.
(1)求作此残片所在圆(不写作法,保留作图痕迹);
(2)求(1)中所作圆的半径.
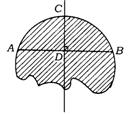
10.(绍兴市)如图,⊙O的直径AB=6,弦CD⊥AB于H(AH<HB),![]() 分别切⊙O、AB、CD于点E、F、G.
分别切⊙O、AB、CD于点E、F、G.
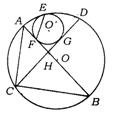
(1)已知CH=2![]() ,求cosA的值.
,求cosA的值.
(2)当AF·FB=AF+FB时,求EF的长;
(3)设BC=M,![]() 的半径为n,用含m的代数式表示n.
的半径为n,用含m的代数式表示n.
11.(温州市)如图,△ACF内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点E.
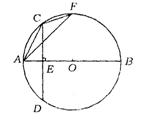
(1)求证:∠ACE=∠AFC;
(2)若CD=BE=8,求sin∠AFC的值.
12.(广东省)已知,如图,A是直线l外的一点,

求作:(1)一个⊙A,使得它与l有两个不同的交点B、C;
(2)一个等腰△BCD,使得它内接于⊙A(说明:要求写出作法.)
13.(镇江市)如图,已知△ABC,其中AB=AC.
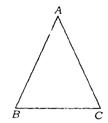
(1)作AB的垂直平分线DE,交AB于点D,AC于点E;连结BE.(尺规作图,不写作法,保留作图痕迹.)
(2)在“(1)”的基础上,若AB=8,△BCE的周长为14,求BC的长.
参考答案
一、选择题
1.C 2.D 3.B 4.D 5.B 6.C
二、填空题
1.![]()
三、解答题:
1.(1)连结OD ∵ AB是⊙O的直径,弦DF⊥AB于点H,∴ ![]() =
=![]() =
=![]()
![]()
∴ ∠1=∠2 ∴ ∠POD=∠PCE ∵ ∠DPO=∠EPC ∴ △PDO∽△PCE
![]() 即PD·PC=PO·PE由切割定理的推论,得PA·PB=PD·PC
即PD·PC=PO·PE由切割定理的推论,得PA·PB=PD·PC
(2)由(1)知,AB是弦DF的垂直平分线,∴ ED=EF,∠3=∠4 ∵![]() ,
,
∴∠3=∠4=![]() 由 ∠5=∠4=
由 ∠5=∠4=![]() ,∠P=
,∠P=![]() ,得∠2=
,得∠2=![]() ∴∠1=
∴∠1=![]() 在Rt△DHO中,由∠1=
在Rt△DHO中,由∠1=![]() ,OD=2,可求得OH=1,DH=
,OD=2,可求得OH=1,DH=![]() ∵△DHO∽△DEC ∴
∵△DHO∽△DEC ∴![]()
∴![]() 解得EC=
解得EC=![]() ∴ CF=CE+EF=CE+DE=
∴ CF=CE+EF=CE+DE=![]()
2.(1)证法一:连结OE
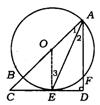
∵ AE平分∠BAF,∴∠1=∠2
∵ OE=OA,∴ ∠1=∠3
∴ ∠3=∠2 ∴ OE∥AD
∵
AD⊥CD,可证∠OED=90![]()
∵ E为⊙O上的点,∴ CD与⊙O相切于点E
证法二:连结BF、OE交于点G
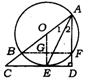
∵ AE平分∠BAF,∴ ∠1=∠2
∴ ![]() ∴ OE⊥BF
∴ OE⊥BF
∵ AB是直径,∴ ∠AFB=90![]()
∴ OE∥AD
以下同证法一
证法三:连结BE、OE
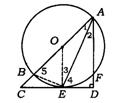
∵ AE平分∠BAF,∠1=∠2
∵
AB是直径,∴ ∠AEB=90![]()
∴
∠1+∠5=90![]()
∴
CD⊥AD,∴ ∠2+∠4=90![]()
∴ ∠5=∠4
∵ OA=PE,∴ ∠1=∠3
∴ ∠4+∠3=90![]() ∴ OE⊥CD
∴ OE⊥CD
∵ E为⊙O上的点,∴ CD与⊙O相切于点E.
(2)解法一:过点D作DG∥AC交AE延长线于G点,连结BE、OE
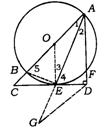
∴ ∠1=∠G,∠G=∠BEC
∵ CD与⊙O相切于点E,∴ ∠BEC=∠1
∴ ∠BEC=∠G ∴ △BEC∽△EGD
∴
![]() ∴ CB·DG=DE·CE
∴ CB·DG=DE·CE
∵ ∠1=∠2=∠G ∴ AD=DG=3
∵
CE·DE=![]() ,∴BC=
,∴BC=![]()
由(1)证得OE∥AD ∴ ![]() 设OE=x(x>0),则CO=
设OE=x(x>0),则CO=![]() +x=
+x=![]() ,CA=+2x=
,CA=+2x=![]() ∴
∴ ![]() 整理,得8
整理,得8![]() -7x-15=0 解得
-7x-15=0 解得![]() =-1(舍负),
=-1(舍负),![]() ∴⊙O的直径为
∴⊙O的直径为![]() ∴ CA=CB+BA=5 由切割线定理,得
∴ CA=CB+BA=5 由切割线定理,得![]() =CB·CA=
=CB·CA=![]() ∴DE=
∴DE=![]() ·
·![]() ,
,
在Rt△ADE中,tan∠AED=![]()
解法二:连结BE、OE、DF可证Rt△BAE∽△EAD
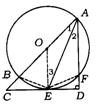
∴ ![]() 即
即![]() ①
①
∵ CD与⊙O相于点E,∴ ∠CEB=∠1
又∠C是公共角, △CBE∽△CEA
∴ ![]() ②
②
由①、②,得![]() =1 ∴ DE∠CE=AD·CB
=1 ∴ DE∠CE=AD·CB
∵ CE·DE=![]() ,AD=3,∴ CB=
,AD=3,∴ CB=![]() 以下同解法一.
以下同解法一.
3.(1)分别作![]() 于点D,
于点D,![]() 于点E,则AB=2AD,AC=2AE,
于点E,则AB=2AD,AC=2AE,
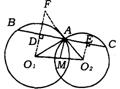
∵ AM⊥BC, ∴ ![]() ∥AM∥
∥AM∥![]() ,∵M为
,∵M为![]() 的中点,
的中点,
∴ AD=AE ∴ AB=AC
(2)∵ ![]() 切⊙
切⊙![]() 于点A, ∴
于点A, ∴ ![]() ⊥
⊥![]() ,又M为
,又M为![]() 的中点,
的中点,
∴ ![]() =2AM.在梯形
=2AM.在梯形![]() ED中,
ED中,![]() ,∴
,∴![]() ,
,
即d1+d2=![]()
(3)证法一:∵ ![]() , ∴ ∠AO
, ∴ ∠AO![]() D=∠
D=∠![]() ,∴ Rt△
,∴ Rt△![]() ∽Rt△
∽Rt△![]()
∴![]() 即
即![]() ,∴AD·AE=
,∴AD·AE=![]() ,
,
由(1)、(2)知AD=AE=1,![]() ,∴
,∴ ![]() ,
,
∴ ![]()
证法二:
由证法一知AD=AE=1,∴ DE=2延长O![]() A交
A交![]() 的延长线于点F,则
的延长线于点F,则![]() =
=![]()
∴![]() =
=![]() ∴
∴ ![]() ,∴ Rr=
,∴ Rr=![]() 在Rt△
在Rt△![]() 中R
中R![]() ∴ R
∴ R![]() .
.
4.(1)连结BF、CE. ∵ TA、TB是⊙O![]() 的切线,∴ TA=TB 同理TA=TC.
的切线,∴ TA=TB 同理TA=TC.
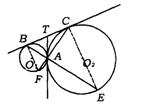
∵TA=TB=TC.∴ △ABC是直角三角形.
∴ AC⊥AB ∴∠BAF=∠CAE=Rt∠ ∴ BF、CE分别是⊙O![]() 、⊙O
、⊙O![]() 、的直径.
、的直径.
∴ BF⊥BC,CE⊥BC ∴ BF∥CE
AB·AC=AE·AF
∴ Rt△ABF∽△AEC ∴ ![]() ∴ AB·AC=AE·AF
∴ AB·AC=AE·AF
(2)∵ △ABF∽△AEC ∴ ![]() =
=![]() 设AB=k,则AE=3k
设AB=k,则AE=3k
∴ BE=4k,∵ TA=TB=TC, ∴ BC=2TA=4 ∵ BC=BA·BE,即时6=±k(k=-2舍去) ∴AE=3k=6
5.解法一:如图,连结OF、BP ∵ AD与半圆相切于F,∴ OF⊥AD, ∵ 四边形ABCD是矩形,四边形ABOF的矩形,∴ AB=OF=![]() BC=5厘米, ∴ BC是半圆的直径,∴
BC=5厘米, ∴ BC是半圆的直径,∴ ![]() 设PE=x厘米,EC=y厘米 则
设PE=x厘米,EC=y厘米 则![]() ,
,
∴![]() ①
①
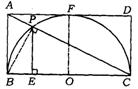
∵ ∠PCE=∠ACB,∠ABC=∠PEC=![]() ∴△ABC∽△PEC ∴
∴△ABC∽△PEC ∴![]() 则
则![]() ,y=2x ② 由①、②解得:
,y=2x ② 由①、②解得:![]() (舍去),
(舍去),![]() ,∴ PE=4厘米 ∴ 点P到BC距离为4厘米.
,∴ PE=4厘米 ∴ 点P到BC距离为4厘米.
解法二:连结OF ∵ AD切半圆O于F,∴OF⊥AD,∵四边形ABCD是矩形,∴四边形ABOF是矩形,∴ AB=OF=![]() BC=5厘米.在Rt△ABC中,AC=
BC=5厘米.在Rt△ABC中,AC=![]() 厘米 ∵ BC是半圆的直径,AB⊥BC,AB的半圆O的切线,由切割线定理得AB
厘米 ∵ BC是半圆的直径,AB⊥BC,AB的半圆O的切线,由切割线定理得AB![]() ,∵
,∵ ![]()
![]() ∵ PC=AC-AP=4
∵ PC=AC-AP=4![]() 厘米,∵ AB⊥BC,PE⊥BC,∴ PE∥AB,∴
厘米,∵ AB⊥BC,PE⊥BC,∴ PE∥AB,∴![]() ,∵ EC=2P在Rt△PEC中,PE
,∵ EC=2P在Rt△PEC中,PE![]() ∴ PE=4厘米∴ 点P到BC距离为4厘米.
∴ PE=4厘米∴ 点P到BC距离为4厘米.
6.(1)证法一:连结![]() .∵BC是⊙
.∵BC是⊙![]() 的切线,∴ ∠
的切线,∴ ∠![]() BC=
BC=![]() ∵ 四边形A
∵ 四边形A![]() BC是⊙
BC是⊙![]() 的内接四边形,∴∠
的内接四边形,∴∠![]() BC+∠
BC+∠![]() AC=
AC=![]() ∴ ∠
∴ ∠![]() AC=
AC=![]() ∴ AC是⊙
∴ AC是⊙![]() 的切线.
的切线.
证法二:连结![]() A、
A、![]() C ∵ BC是⊙
C ∵ BC是⊙![]() 的切线,∴∠
的切线,∴∠![]() BC=
BC=![]() ∴ ⊙
∴ ⊙![]() 是⊙
是⊙![]() 的直径∴∠
的直径∴∠![]() AC=
AC=![]() ∴ AC是⊙
∴ AC是⊙![]() 的切线.
的切线.
(2)证明:连结AB ∵ PC切⊙![]() 于点A,∴ ∠PAD=∠ABD又∵ ∠AC
于点A,∴ ∠PAD=∠ABD又∵ ∠AC![]() =∠AB
=∠AB![]() ,
,
∴∠PAD=∠A C![]() ,∴ AD∥
,∴ AD∥![]() .
.
(3)解法一:∵ PC是⊙![]() 的切线,PB是⊙
的切线,PB是⊙![]() 的割线,∴ PA
的割线,∴ PA![]() =PD·PB,∵PD=1,PB=5,∴ PC是⊙
=PD·PB,∵PD=1,PB=5,∴ PC是⊙![]() 的切线,∴AD∥
的切线,∴AD∥![]() C.∴
C.∴ ![]() ∴
∴ ![]() ∴ AC=2
∴ AC=2![]()
解法二:同解法一,得PA=![]() ,∵AC、BC分别切⊙
,∵AC、BC分别切⊙![]() 于点A、B,∴ AC、BC分别切⊙
于点A、B,∴ AC、BC分别切⊙![]() 于点A、B,∴
于点A、B,∴ ![]() B⊥BC,
B⊥BC,![]() A⊥PC∴∠PBC=∠PA
A⊥PC∴∠PBC=∠PA![]() =
=![]() 又∴ ∠P=∠P,∴ Rt△PBC∽Rt△PA
又∴ ∠P=∠P,∴ Rt△PBC∽Rt△PA![]() ∴
∴![]() ∴
∴![]() ∴ BC=2
∴ BC=2![]()
7.证法一(1)证明:连结OC,∵ PC2=PE·PO,∵ ![]() ,∠P=∠P,∴ △PCE∽△POC,∴ ∠PEC=∠PCO又∵ CD⊥AB,∴ ∠PEC=
,∠P=∠P,∴ △PCE∽△POC,∴ ∠PEC=∠PCO又∵ CD⊥AB,∴ ∠PEC=![]() ,∴ ∠PCO=
,∴ ∠PCO=![]() ,∴ PC是⊙O的切线.
,∴ PC是⊙O的切线.
(2)解:设OE=x,∵ OE∶EA=1∶2,EA=2x,OA=OC=3x,∴ OP=3 x+6.又∵ CE是高,∴ Rt△OCE∽Rt△OPC,![]() ,
,
∴ OC![]() (或由射影定理得)即
(或由射影定理得)即 ![]()
∴ ![]()
![]() .
.
(3)连结AD,∵ AB⊥CD,∴![]() =
=![]() ,∠PCA=∠ADC=∠ACE,
,∠PCA=∠ADC=∠ACE,
∴ sin∠PCA=sin∠ADC=![]() ,而AE=2,OE=1,OC=3,
,而AE=2,OE=1,OC=3,
∴ AC=![]()
∴ sin∠PCA=![]()
证法二(1)同上
(2)过点A作AF⊥PC于F,连结AD,∴ ∠ACP=∠CDA,又∵ CD⊥AB,∴ ∠CDA=∠DCA,∴ ∠DCA=∠ACP,∴ 点A为∠DCA=∠ACP,∴ 点A为∠DCP平分线上的点,∴ AE=AF,又∵ OE∶EA=1∶2,AP=6,设OE=x,∴ EA=2 x,AF=2 x,即OA=3 x,又∵ Rt△PCO∽Rt△PFA,∴ ![]() ,∴
,∴ ![]() ,解得
,解得![]() (舍去),∴ OA=3 x=3.
(舍去),∴ OA=3 x=3.
(3)∵ AE=2 x=2,CE2=x(2 x+6)=8,∴ CE=2![]() ,AE=2,
,AE=2,
∵ PE=8,∴ AC=2![]() ,∴ sin∠PCA=
,∴ sin∠PCA=![]() =
=![]() .
.
证法三:(1)同上
(2)连结BC,∵ OE∶EA=1∶2,设OE=x,EA=2 x,在Rt△OCP中,
∵ CE⊥AB于E,∴ CE2=OE·EP=x(6+2x),在Rt△BCA中,
CE2=BE·EA=4 x·2 x.∴ x(6+2 x)=4 x·2 x.解得x 1=1,x 2=0(舍去)∴ OA=3 x=3.
(3)在Rt△BCE中,易证:CE=2![]() ,
,![]() .又
.又
∵ ∠PCA=∠CBA,∴ sin∠PCA=sin∠CBA=![]() .
.
证法四:(1)同上
(2)∵ OE∶EA=1∶2,设OE=x,∴ EA=2x,∵ Rt△POC中,CD⊥PB,∴ CE![]() ,又∵ 由(1)得证PC是⊙O的切线,∴ PC
,又∵ 由(1)得证PC是⊙O的切线,∴ PC![]() =PA·PB=6(6+x),解得
=PA·PB=6(6+x),解得![]() (舍去), OA=3x=3.
(舍去), OA=3x=3.
(3)易证:∠PCA=∠DCA,∵ CE![]() =8,CE=2
=8,CE=2![]() ,EA=2,AC=2
,EA=2,AC=2![]()
∴ sin∠DCA=sin∠PCA=![]()
8.(1)∵ PB切⊙O于点B,∠PBC=∠A,∵ PF为∠APB的角平分线,∴ ∠APE=∠BPD,
∴ △BPD∽△APE
(2)∵ △BPD∽△APE,∴ ∠BDP=∠AEP,∴ ∠BED=∠BDE,∴ BE=BD.又∵ BD·AE=2![]() ,∴ BE·AE=2
,∴ BE·AE=2![]() ,∴ FE·AE=2
,∴ FE·AE=2![]() .
.
(3)∵ △BPD∽△APE,∴ ![]() ,又∵ AB是⊙O的直径,PB⊙O于点B,∴ ∠ABP=
,又∵ AB是⊙O的直径,PB⊙O于点B,∴ ∠ABP=![]() .而∠A=
.而∠A=![]() ∴ sin∠A=sin
∴ sin∠A=sin![]() =
=![]() ,∴
,∴ ![]() 又BD=BE,∴
又BD=BE,∴ ![]() 又BE·AE
又BE·AE![]() ,∴ AE=2,BE=
,∴ AE=2,BE=![]() ,∴ AB=2+
,∴ AB=2+![]() ,tan
,tan![]()
![]() ,∴ PB
,∴ PB![]() +3,∴ tan∠BDE=tan∠BED=
+3,∴ tan∠BDE=tan∠BED=![]()
9.(1)如图
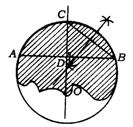
(2)设所作圆的圆心为O,连结OB,设⊙O的半径为r
则OB=r,OD=r-CD=r-8
∵ CD⊥AB,AB=24,∴ BD=![]() AB=12在Rt△OBD中,由勾股定理得:OD2+BD2=OB2即(r-8)2+122=r2,解之得r=13,∴ 所作圆的半径为13厘米.
AB=12在Rt△OBD中,由勾股定理得:OD2+BD2=OB2即(r-8)2+122=r2,解之得r=13,∴ 所作圆的半径为13厘米.
10.解:(1)∵ AB是⊙O的直径,∴ ∠ACB=90°.又∵ CD⊥AB,∴ CH2=AH·HB=AH(AB-AH),∴ ![]() =AH(6-AH),AH2-6AH+8=0,∴ AH=2或AH=4(不合,舍去).
=AH(6-AH),AH2-6AH+8=0,∴ AH=2或AH=4(不合,舍去).
∴ CA2=AH·AB=2×6=12,∴ CA=![]() .∴ cosA=
.∴ cosA=![]() =
=![]() .
.
(2)∵ AF·BF=AF+FB,又AF+FB=AB=6,则AF<FB,∴ AF=3-![]() ,FB=3+
,FB=3+![]() .连结O′F,O′G,OE,∵ ⊙O′分别切AB、CD于F,G切⊙O于E,∴ O,O′,E三点共线.∴ ∠O′FH=∠O′GH=90°.又CD⊥AB,O′F=O′G,∴ 四边形FHGO′是正方形.
.连结O′F,O′G,OE,∵ ⊙O′分别切AB、CD于F,G切⊙O于E,∴ O,O′,E三点共线.∴ ∠O′FH=∠O′GH=90°.又CD⊥AB,O′F=O′G,∴ 四边形FHGO′是正方形.
设⊙O′的半径为r,在Rt△OO′F中,OO′-O′F2=FO2=(BF-OB)2,(3-r)2-r2=(3+![]() -3)2,∴ r=1.从而OO′=2,∴ ∠FOO′=30°,∠FO′O=60°,∵ O′E=O′F.∴ ∠E=
-3)2,∴ r=1.从而OO′=2,∴ ∠FOO′=30°,∠FO′O=60°,∵ O′E=O′F.∴ ∠E=![]() ∠FO′O=30°.∴ ∠E=∠FOO′.∴ EF=FO-
∠FO′O=30°.∴ ∠E=∠FOO′.∴ EF=FO-![]() .
.
(3)由射影定理得BC2=AH·AB=6(BF-FH)=6(BF-n). ①
∵ O′O2-O′F2=OF2,∴ (3-n )2-n2=(BF-3)2,9-6n=BF2-6BF+9,BF2=6(BF-n) ②
由①②得BF2=BC2,∴ BF=BC,∴ BC2=6(BC-n),∴ m2=6(m-n),即n=-![]() m2+m.
m2+m.
11.(1)证法一:∵ AB是⊙O的直径,CD⊥AB,∴ ![]() =
=![]() ,∴ 又∵ CD⊥AB,∵∠ACE=∠B,∵ ∠B=∠AFC,∴∠ACB=∠AFC.
,∴ 又∵ CD⊥AB,∵∠ACE=∠B,∵ ∠B=∠AFC,∴∠ACB=∠AFC.
(2)解:∵ AB是⊙O的直径,CD⊥AB,∴ CE=DE,∵CD=BE=8,∴ CE=DE=4,由相交弦定理,得AE·BE=CE·DE,∴ 8AE=16,∴ AE=2.在Rt△ACE中,AC=![]() =
=![]() =
=![]() (也可用AC2=AB·AE来求)
(也可用AC2=AB·AE来求)
∴ sin∠ACE=![]() .
.
又∵∠AFC=∠ACE,sin∠AFC=![]() .
.
12.(1)作法:①在l外取一点E,使点E、A在l的两侧,②以点A为圆心,AE长为半径,作圆交l于B、C两点.则⊙A即为所求.
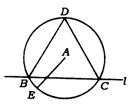
(2)①以点B为圆心,BC长为半径画弧,交⊙A于点D,②连结BD和CD.则△BCD即为所求.
13.(1)作出AB的垂直平分线,标出点D,E,连结BE.
(2)由(1),得BE=AE,∵ AB=AC,∴ BC+BE+EC=BC+AE+EC=BC+AC=BC+AB=BC+18=14.∴ BC=6