中考数学真题演练8
一、选择题
1.(北京市朝阳区)用科学计算器算得①293=24389;②![]() ≈7.;③sin35°≈0.;④若tanα=5,则锐角α≈0.°.其中正确的是 ( )
≈7.;③sin35°≈0.;④若tanα=5,则锐角α≈0.°.其中正确的是 ( )
(A)①②③ (B)①②④
(C)②③④ (D)①③④
2.(北京市朝阳区)平行四边形ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为 ( )
(A)(1,-2) (B)(2,-1)
(C)(1,3) (D)(2,-3)
3.(河北省)已知一个直角三角形的两条直角边的长恰好是方程2x2-8x+7=0的两个根,则这个直角三角形的斜边长是 ( )
(A)![]() (B)3 (C)6 (D)9
(B)3 (C)6 (D)9
4.(沈阳市)面积为2的△ABC,一边长为x,这边上的高为y,则y与x的变化规律用图象表示大致是 ( )
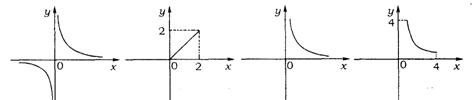
(A) (B) (C) (D)
5.(陕西省)如图所示,以数轴的单位长线段为边作一个正方形,以数轴的原点为圆心、正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是 ( )
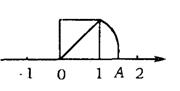
(A)![]() (B)1.4 (C)
(B)1.4 (C)![]() (D)
(D)![]()
6.(福州市)已知:二次函数y=x2+bx+c与x轴相交于A(x1,0)、B(x2,0)两点,其顶点坐标为P(![]() ),AB=x1-x2,若S△APB=1,则b与c的关系式是 ( )
),AB=x1-x2,若S△APB=1,则b与c的关系式是 ( )
(A)b2-4c+1=0 (B)b2-4c-1=0
(C)b2-4c+4=0 (D)b2-4c-4=0
7.(苏州市)如图,已知△ABC中,BC=8,BC上的高h=4,D为BC上一点,EF∥BC,交AB于点E,并AC于点F(EF不过A、B).设E到BC的距离为x,则△DEF的面积y关于x的函数的图象大致为 ( )
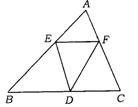
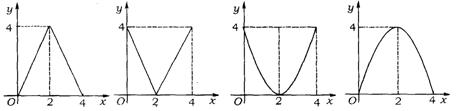
(A) (B) (C) (D)
8.(绍兴市)已知关于x的一元二次方程x2-(R+r)x+![]() d2=0没有实数根,其中R、r分别为⊙O1、⊙O2的半径,d为此两圆的圆心距,则⊙O1、⊙O2的位置关系是 ( )
d2=0没有实数根,其中R、r分别为⊙O1、⊙O2的半径,d为此两圆的圆心距,则⊙O1、⊙O2的位置关系是 ( )
(A)外离 (B)相切 (C)相交 (D)内含
9.(绍兴市)抛物线y=ax2+bx+c与x轴交于A、B两点,Q(2,k)是该抛物线上一点,且AQ⊥BQ,则ak的值等于 ( )
(A)-1 (B)-2 (C)-2 (D)3
10.(常州市)在实数2,sin30°,![]() ,-
,-![]() 中,有理数的个数是 ( )
中,有理数的个数是 ( )
(A)2个 (B)3个 (C)4个 (D)1个
二、填空题
1.(重庆市)给出下列四个命题
①以![]() 、2、
、2、![]() 为边长的三角形是直角三角形;
为边长的三角形是直角三角形;
②函数y=![]() 的自变量x的取值范围是x≥-
的自变量x的取值范围是x≥-![]() ;
;
③若ab>0,则直线y=ax+b必过二、三象限;
④相切两圆的连心线必过切点.
其中正确命题的序号是________.
2.(河北省)有一面积为60的梯形,其上底长是下底长的![]() .若下底长为x,高为y,则y与x的函数关系式是________.
.若下底长为x,高为y,则y与x的函数关系式是________.
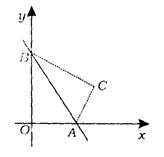
3.(山东省)如图,直线y=-![]() +
+![]() 与x轴、y轴分别交于A、B两点,若把△AOB沿直线AB翻折,点O落在C处,则点C的坐标是________.
与x轴、y轴分别交于A、B两点,若把△AOB沿直线AB翻折,点O落在C处,则点C的坐标是________.
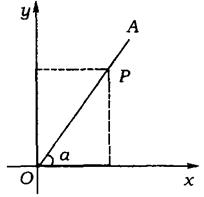
4.(江西省)如图,P是∠α的边OA上一点;且P点坐标为(3,4),则sinα=_________,cosα=_________.
5.(新疆乌鲁木齐)2sin45°+(![]() )0-
)0-![]() =_________.
=_________.
6.(绍兴市)若一个三角形的三边长均满足方程x2-6x+8=0,则此三角形的周长为________.
三、解答题:
1.(陕西省)计算20+2sin45°-![]() .
.
2.(北京市东城区)计算:![]() -sin60°+(-2
-sin60°+(-2![]() )0-
)0-![]() .
.
3.(北京市东城区)在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a、b是关于x的一元二次方程x2-mx+2m-2=0的两个根,求Rt△ABC中较小锐角的正弦值.
4.(北京市西城区)已知:在平面直角坐标系xOy中,点A(0,4),点B和点C在x轴上(点B在点C的左边),点C在原点的右边,作BE⊥AC,垂足为E(点E在线段AC上,且点E与点A不重合),直线BE与y轴交于点D,若BD=AC.
(1)求点B的坐标;
(2)设OC长为m,△BOD的面积为S,求S与m的函数关系式,并写出自变量m的取值范围;
(3)当m=5时,求点D的坐标及sin∠BDO的值.
5.(北京市海淀区)计算:![]() (2cos45°-sin90°)+(4-5π)0-(
(2cos45°-sin90°)+(4-5π)0-(![]() -1)-1.
-1)-1.
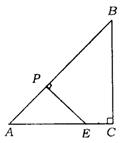
6.(北京市海淀区)如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,且点P不与点A重合,过点P作PE⊥AB交AC边于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式.
7.(北京市海淀区)已知:二次函数y=x2-kx+k+4的图象与y轴交于点C,且与x轴的正半轴交于A、B两点(点A在点B左侧).若A、B两点的横坐标为整数,
(1)确定这个二次函数的解析式并求它的顶点坐标;
(2)若点D的坐标是(0,6),点P(t,0)是线段AB上的一个动点,它可与点A重合,但不与点B重合,设四边形PBCD的面积为S,求S与t的函数关系式;
(3)若点P与点A重合,得到四边形ABCD,以四边形ABCD的一边为边,画一个三角形,使它的面积等于四边形ABCD的面积,并注明三角形高线的长.再利用“等底等高的三角形面积相等”的知识,画一个三角形,使它的面积等于四边形ABCD的面积(画示意图,不写计算和证明过程).
8.(北京市朝阳区)已知:如图,△ABC内接于⊙O,AD是⊙O的直径,点E、F分别在AB、AC的延长线上,EF交⊙O于点M、N,交AD于点H,H是OD的中点,![]() =
=![]() ,EH-HF=2.设∠ACB=α,tanα=
,EH-HF=2.设∠ACB=α,tanα=![]() ,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
,EH和HF是方程x2-(k+2)x+4k=0的两个实数根.
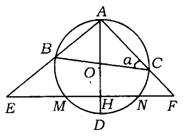
(1)求EH和HF的长;
(2)求BC的长.
9.(北京市朝阳区)已知:以直线x=1为对称轴的抛物线与x轴交于A、B两点(点A在点B的左边),且经过点(4,![]() )和(0,-
)和(0,-![]() ).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
).点P(x,y)在抛物线的顶点M的右侧的半支上(包括顶点M),在x轴上有一点C使△OPC是等腰三角形,OP=PC.
(1)若∠OPC是直角,求点P的坐标;
(2)当点P移动时,过点C作x轴的垂线,交直线AM于点Q,设△AQC的面积为S,求S关于x的函数解析式和自变量x的取值范围,并画出它的图象.
10.(上海市)如图,直线y=![]() x+2分别交x、y轴于点A、C,P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,S△ABP=9.
x+2分别交x、y轴于点A、C,P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,S△ABP=9.
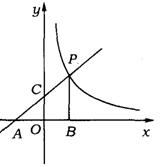
(1)求点P的坐标;
(2)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧.作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
11.(天津市)已知抛物线y=2x2-3x+m(m为常数)与x轴交于A、B两点,且线段AB的长为![]() .
.
(1)求m的值;
(2)若该抛物线的顶点为P,求△ABP的面积.
12.(重庆市)如图,已知两点A(-8,0),B(2,0),以AB为直径的半圆与y轴正半轴交于点C.
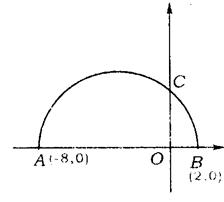
(1)求过A、C两点的直线的解析式和经过A、B、C三点的抛物线的解析式;
(2)若点D是(1)中抛物线的顶点,求△ACD的面积.
13.(哈尔滨市)当x=sin30°,y=tan60°,先化简,再求代数式(![]() -
-![]() )÷
)÷![]() 的值.
的值.
14.(哈尔滨市)如图,△ABC内接于⊙O,BC=4,S△ABC=6![]() ,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧
,∠B为锐角,且关于x的方程x2-4xcosB+1=0有两个相等的实数根.D是劣弧![]() 上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.
上任一点(点D不与点A、C重合),DE平分∠ADC,交⊙O于点E,交AC于点F.
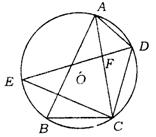
(1)求∠B的度数;
(2)求CE的长;
(3)求证:DA、DC的长是方程y2-DE·y+DE·DF=0的两个实数根.
15.(陕西省)如图,已知点A(tanα,0),B(tanβ,0),在x轴正半轴上,点A在点B的左边,α、β是以线段AB为斜边,顶点C在x轴上方的Rt△ABC的两个锐角.
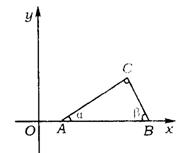
(1)若二次函数y=-x2-![]() kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
kx+(2+2k-k2)的图象经过A、B两点,求它的解析式;
(2)点C在(1)中求出的二次函数的图象上吗?请说明理由.
16.(甘肃省)如图,在△ABC中,AB=4,BC=3,∠B=90°,点D在AB上运动,但与A、B不重合,过B、C、D三点的圆交AC于E,连结DE.
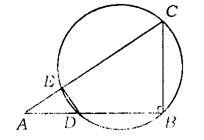
(1)设AD=x,CE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)当AD长为关于x的方程2x2+(4m+1)x+2m=0的一个整数根时,求m的值.
17.(山东省)已知直线y=![]() x+4与x轴、y轴的交点分别为A、B.又P(0,-1)Q(0,k),其中0<k<4.再以Q点为圆心,PQ的长为半径作圆,则当k取何值时,⊙Q与直线AB相切?
x+4与x轴、y轴的交点分别为A、B.又P(0,-1)Q(0,k),其中0<k<4.再以Q点为圆心,PQ的长为半径作圆,则当k取何值时,⊙Q与直线AB相切?
18.(安徽省)求直线y=3-x与圆x2+y2=5的交点的坐标.
19.(江西省)已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(m,0),B(n,0),且m+n=4,![]() =
=![]() .
.
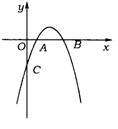
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过C作一条平行于x轴的直线交抛物线于另一点P,求△ACP的面积S△ACP.
20.(福州市)已知:矩形ABCD在平面直角坐标系中,顶点A、B、D的坐标分别为A(0,0),B(m,0),D(0,4),其中m≠0.
(1)写出顶点C的坐标和矩形ABCD的中心P点的坐标(用含m的代数式表示);
(2)若一次函数y=kx-1的图象l把矩形ABCD分成面积相等的两部分,求此一次函数的解析式(用含m的代数式表示):
(3)在(2)的前提下,l又与半径为1的⊙M相切,且点M(0,1),求此时矩形ABCD的中心P点的坐标.
21.(长沙市)计算:![]() +(
+(![]() +1)0-2sin45°.
+1)0-2sin45°.
22.(成都市)计算:2sin45°-![]() - -tan60° +
- -tan60° +![]() .
.
23.(成都市)如图,Rt△ABO的顶点A是双曲线y=![]() 与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=
与直线y=-x-(k+1)在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
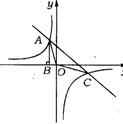
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△ABC的面积.
24.(成都市)已知抛物线y=x2和直线y=(m2-1)x+m2.
(1)当m为何实数时,抛物线与直线有两个交点?
(2)设坐标原点为O,抛物线与直线的交点从左至右分别为A、B,当抛物线与直线两交点的横坐标之差为3时,求三角形AOB中OB边上的高.
25.(成都市)已知:如图,在半径为r的半圆O中,半径OA⊥直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与B、A重合.
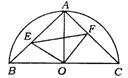
(1)求证:S四边形AEOF=![]() r2;
r2;
(2)设AE=x,S△OEF=y,写出y与x之间的函数解析式,并求出自变量x的取值范围;
(3)S△OEF=![]() S△ABC时,求点E、F分别在AB、AC上的位置及E、F两点间的距离.
S△ABC时,求点E、F分别在AB、AC上的位置及E、F两点间的距离.
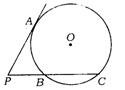
26.(镇江市)如图,PA切⊙Q于点A,PBC交⊙Q于点B、C.若PB、PC的长是关于x的方程x2-(m-2)x+(m+2)=0的两个根,且BC=4,求m的值以及PA的长.
27.(扬州市)计算:sin60°-![]() -
-![]() -(
-(![]() )-1.
)-1.
28.(扬州市)如图,抛物线y=-ax2+ax+6a交x轴负半轴于点A,交x轴正半轴于点B,交y轴正半轴于点D,O为坐标原点,抛物线上一点C的横坐标为1.
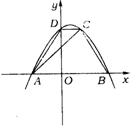
(1)求A、B两点的坐标;
(2)求证:四边形ABCD是等腰梯形;
(3)如果∠CAB=∠ADO,求a的值.
29.(扬州市)如图,在平面直角坐标系中,以点A(-1,0)为圆心,AO为半径的圆交x轴负半轴于另一点B,点F在⊙A上,过点F的切线交y轴正半轴于点E,交x轴正半轴于点C,已知CF=2![]() .
.
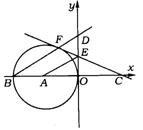
(1)求点C的坐标;
(2)求证:AE∥BF;
(3)延长BF交y轴于点D,求点D的坐标及直线BD的解析式.
30.(绍兴市)已知α是锐角,且tanα,cotα是关于x的一元二次方程x2-kx+k2-8=0的两个实数根,求k的值.
31.(绍兴市)如图,已知平面直角坐标系中三点A(4,0),B(0,4),P(x,0)(x<0),作PC⊥PB交过点A的直线l于点C(4,y).
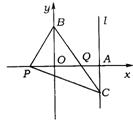
(1)求y关于x的函数解析式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标.
32.(广东省)如图,在△ABC中,∠B=90°,AB=4,BC=3,O是AB的中点,OP⊥AB交AC于点P.
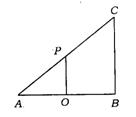
(1)证明线段AO、OB、OP中,任意两条线长度之和大于第三条线段的长度;
(2)过线段OB(包括端点B)上任一点M,作MN⊥AB交AC于点N,如果要使线段AM,MB,MN中任意两条线段长度之和大于第三条线段的长度,那么请求出线段AM的长度的取值范围.
参考答案
一、选择题
1.A 2.A 3.B 4.C 5.D 6.D 7.D 8.A 9.A 10.B
二、填空题
1.③④ 2.![]() 3.
3.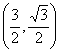 4.
4.![]() ,
,![]() 5.2 6.6,10,12
5.2 6.6,10,12
三、解答题:
1.2 2.2 3.![]()
4.~9.(略)
10.(1)由题意,得点C(0,2),点A(-4,0).设点P的坐标为(a,![]() a+2),其中a>0.由题意,得S△ABP=
a+2),其中a>0.由题意,得S△ABP=![]() (a+4)(
(a+4)(![]() a+2)=9.解得a=2或a=-10(舍去).而当a=2时,
a+2)=9.解得a=2或a=-10(舍去).而当a=2时,![]() a+2=3,∴ 点P的坐为(2,3).
a+2=3,∴ 点P的坐为(2,3).
(2)设反比例函数的解析式为y=![]() ,∵ 点P在反比例函数的图象上,∴ 3=
,∵ 点P在反比例函数的图象上,∴ 3=![]() ,k=6.∴ 反比例函数的解析式为y=
,k=6.∴ 反比例函数的解析式为y=![]() ,设点R的坐标为(b,
,设点R的坐标为(b,![]() ),点T的坐标为(b,0).其中b>2,那么BT=b-2,RT=
),点T的坐标为(b,0).其中b>2,那么BT=b-2,RT=![]() .
.
当△RTB∽△AOC时,![]() =
=![]() ,即
,即![]() =
=![]() =2,∴
=2,∴ ![]() =2.解得b=3或b=-1(舍去).∴ 点R的坐标为(3,2).
=2.解得b=3或b=-1(舍去).∴ 点R的坐标为(3,2).
②当△RTB∽△COA时,![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,∴
,∴ ![]() =2.解得b=1+
=2.解得b=1+![]() 或b=1-
或b=1-![]() (舍去)∴ 点R的坐标为(1+
(舍去)∴ 点R的坐标为(1+![]() ,
,![]() ).
).
综上的述,点R的坐标为(3,2)或(1+![]() ,
,![]() ).
).
11.(1)关于x的方程2x2+3x+m=0,判别式△=(-3)2-8m=9-8m>0,得m=![]() ,x1+x2=
,x1+x2=![]() x1·x2=
x1·x2=![]() .∴ AB=x1-x2=
.∴ AB=x1-x2=![]() =
=![]() .根据题意,AB=
.根据题意,AB=![]() =
=![]() ,∴ m=1.
,∴ m=1.
(1)∵ m=1,∴ 抛物线为y=2x2+3x+1,其顶点P的纵坐标为yp=![]() =-
=-![]() ,
,
∴ S△ABP=![]() ·AB·yp=
·AB·yp=![]() ×
×![]() ×
×![]() =
=![]() .
.
12.解:连结AC、BC,∵AB是直径,∴ ∠ACB=90°,又CO⊥AB,∴ Rt△AOC∽Rt△COB,
∴ CO2=AO·BO=8×2=16, ∴ CO=4,故,点C的坐标为(0,4).
(1)设过点A、C的直线的解析式为y=mx+n,将A(-8,0),C(0,4)代入得,![]() 得m=
得m=![]() . ∴ 直线的解析式为y=
. ∴ 直线的解析式为y=![]() x+4.
x+4.
∵ 抛物线过点A(-8,0)、B(2,0),故,设抛物线的解析式为y=a(x+8)(x-2).因过点C(0,4),∴ 4=a(0+8)(0-2),∴ a=-![]() .故抛物线的解析式为y=-
.故抛物线的解析式为y=-![]() (x+8)(x-2)=-
(x+8)(x-2)=-![]() x2-
x2-![]() x+4.
x+4.
(2)设抛物线的对称轴交x轴于点H.其顶点横坐标为x=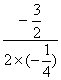 =-3,纵坐标为y=-
=-3,纵坐标为y=-![]() ×9-
×9-![]() ×(-3)+4=
×(-3)+4=![]() .∴ S△ACD=(S△ADH+S梯形COHD)-S△AOC=
.∴ S△ACD=(S△ADH+S梯形COHD)-S△AOC=![]() -
-![]() ×4×8=31-16=15.
×4×8=31-16=15.
13.原式=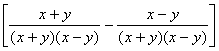 ·
·![]()
=![]() ·
·![]() =
=![]() .
.
把x=sin30°=![]() ,y=tan60°=
,y=tan60°=![]() 代入上式,原式=
代入上式,原式=![]() =
=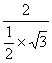 =
=![]() .
.
14.(1)∵ 关于x的方程x2-4cosB+1=0有两个相等的实数根.
∴ △=(-4cosB)2-4=0.
∴ 4cosB=![]() 或=cosB=-
或=cosB=-![]() (舍去),又∵ ∠B为锐角,∴ ∠B=60°.
(舍去),又∵ ∠B为锐角,∴ ∠B=60°.
(2)过点A作AH⊥BC,垂足为H.
S△ABC=![]() BC·AH=
BC·AH=![]() BC·AB·sin60°=6
BC·AB·sin60°=6![]()
即 ![]() ×4×AB×
×4×AB×![]() =6
=6![]() AB=6.
AB=6.
在Rt△ACH中,BH=AB·sin60°=6×![]() =3, AH=AB·sin60°=6×
=3, AH=AB·sin60°=6×![]() =3
=3![]() ∴ CH=BC-BH=4-3-1.
∴ CH=BC-BH=4-3-1.
在Rt△ABH中,AC2=AH2+CH2=27+1=28.
∴ AC=±2![]() (负值舍去).AC=±2
(负值舍去).AC=±2![]() ,
,
∴ 连结AE、在圆内接四边形ABCD中,∠B+∠ADC=180°,∴ ∠ADC=120°.
∵ DE平分∠ADC,∴ ∠EDC=60°=∠EAC=60°,
∵ ∠AEC=∠B=60°∴ ∠AEC=∠EAC,∴ CE=AC=2![]() .
.
(3)在△EDA与△CDF中,∠AED=∠FCD,∠EDA=∠EDC=60°,
∴ △EDA∽△CDF,∴ ![]() =
=![]() ,即DA·DC=DE·DF.
,即DA·DC=DE·DF.
延长CD至G,使DG=DA,连结AG. ∴ ∠ADG=∠B=60°,∴ ∠G=∠GAD=60°.
在△EDA与△CDF中,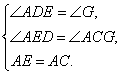 ∴△EDA≌△CGA
∴△EDA≌△CGA
∴ED=CG=GD+DC=CD+DA
∴DA、DC的长是方程y2-DE·y+DE·DF=0的两个实数根.
15.(1)∵
a,β是Rt△ABC的两个锐角,∴ tana.tanβ=1.tana>0,tanβ>0.由题知tana.tanβ是方程x2+![]() kx-(2+2k-k2)=0的两个根,∴
tana·tanβ=-(2+2k-k2)=k2-2k-2.∴
k2-2k-2=1. 解得,k=3或k=-1.而tana·tanβ=-
kx-(2+2k-k2)=0的两个根,∴
tana·tanβ=-(2+2k-k2)=k2-2k-2.∴
k2-2k-2=1. 解得,k=3或k=-1.而tana·tanβ=-![]() k>0,∴ k<0.∴
k=3应舍去,k=-1.
k>0,∴ k<0.∴
k=3应舍去,k=-1.
故所求二次函数的解析式为y=- x2+![]() x-1.
x-1.
(2)不在.过C作CD⊥AB于D.令y=0,得-x2+![]() x-1=0,解得x1=
x-1=0,解得x1=![]() ,x2=2.∴A
,x2=2.∴A![]() ,B(2,0),AB=
,B(2,0),AB=![]() .∴ tanα=
.∴ tanα=![]() ,tanβ=2,设CD=m,则有CD=AD·tanα=
,tanβ=2,设CD=m,则有CD=AD·tanα=![]() AD.∴ AD=2CD.又CD=BD·tanβ=2BD,∴ BD=
AD.∴ AD=2CD.又CD=BD·tanβ=2BD,∴ BD=![]() CD.∴ 2m+
CD.∴ 2m+![]() m=
m=![]() .∴ m=
.∴ m=![]() ,AD=
,AD=![]() .∴ C(
.∴ C(![]() ,
,![]() ).当x=
).当x=![]() 时,y=
时,y=![]() ≠
≠![]() .∴ 点C不在(1)中求出的二次函数的图象上.
.∴ 点C不在(1)中求出的二次函数的图象上.
16.(1)在△ABC中,∠B=90°,AB=4,BC=3,∴ AC=5.
∵ 四边形DBCE为圆内接四边形,∴ ∠AED=∠B.又∠A=A,∴ △ADE∽△ACB,∴ ![]() =
=![]() ,∴ AE=
,∴ AE=![]() =
=![]() x.由CE=AC-AE,得y=-
x.由CE=AC-AE,得y=-![]() x=-
x=-![]() +5.∴ 点D在AB上运动,且与A、B不重合,AB=4,∴ 自变量x的取值范围是0<x<4.
+5.∴ 点D在AB上运动,且与A、B不重合,AB=4,∴ 自变量x的取值范围是0<x<4.
(2)∵ 2x2+(4m+1)x+2m=0,∴ (x+2m)(2x+1)=0,∴ x1=-2m, x2=-![]() .
.
∵ x2=-![]() 是分数,∴ 整数根为-2m,即AD=-2m.
是分数,∴ 整数根为-2m,即AD=-2m.
∵ 0<x<4,即0<AD<4.∴ 满足0<AD<4的整数为1、2、3.
当AD=-2m=1时,m=-![]() ;当AD=-2m=2时,m=-1;当AD=-2m=3时,m=-
;当AD=-2m=2时,m=-1;当AD=-2m=3时,m=-![]() .
.
∵ 方程2x2+(4m+1)x+2m=0的判别式为△=(4m+1)2-16m=(4m-1)2,对任意实数m,恒有(4m-1)2≥0.∴ 所求m的值为-![]() ,-1和-
,-1和-![]() .
.
17.把x=0和y=0分别代入y=![]() x+4,得
x+4,得![]()
![]() ∴ A、B两点的坐标分别为(-3,0),(0,4)∵ OA=3, OB=4,∴ AB=5,BQ=4-k,QP=k+1.作
∴ A、B两点的坐标分别为(-3,0),(0,4)∵ OA=3, OB=4,∴ AB=5,BQ=4-k,QP=k+1.作![]() ⊥AB于
⊥AB于![]() ,当
,当 ![]() =QP时,⊙O与直线AB相切.由Rt△B
=QP时,⊙O与直线AB相切.由Rt△B![]() ∽Rt△BAO,得
∽Rt△BAO,得![]() =
=![]() ,∴
,∴ ![]() =
=![]() ,解得k=
,解得k=![]() ,∴ 当k=
,∴ 当k=![]() 时,⊙O与直线AB相切.
时,⊙O与直线AB相切.
18.联立方程组,得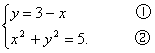
把①代入②并整理,得:x2-3x+2=0.解这个一元二次方程,得x1=1,x2=2.
将x的值分别代入①,得y1=2,y2=1.所以,原方程组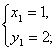
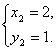 故所求的交点坐标分别为(1,2,),(2,1)
故所求的交点坐标分别为(1,2,),(2,1)
19.解:(1)由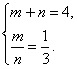 解得
解得![]() 将A(1,0),B(3,0)的坐标分别代入y=-x2+bx+c得
将A(1,0),B(3,0)的坐标分别代入y=-x2+bx+c得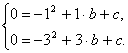 解得b=4,c=-3.
解得b=4,c=-3.
∴ 此抛物线的解析式为y=-x2+4x-3.
(2)抛物线y=-x2+4x-3与y轴相交于点C(0,-3),令y=-3,则有-3=-x2+4x-3,整理得x2-4x=0,解之,得x1=0,x2=4.
∴ 点P坐标为(4,-3),CP=4.∴ S△ACP=![]() ·CP·OC=
·CP·OC=![]() ×4×3=6.
×4×3=6.
20.(1)C点坐标为(m,4),P点坐标为(![]() ,2)
,2)
(2)∵ 直线l把矩形ABCD分成面积相等两部分:∴ l必过中心点P(![]() ,2).∴ 4=km-2,
,2).∴ 4=km-2,
∵ m≠0,∴ k=![]() , ∴ y=
, ∴ y=![]() x-1.
x-1.
(3)设直线l与y轴相交于点F,∴ F点坐标为(0,-1),
∵ ⊙M的半径为1,∴ sin∠EFD=![]() =
=![]() ,∴ ∠EFD=30°,过P作PG⊥y轴于G.∴
,∴ ∠EFD=30°,过P作PG⊥y轴于G.∴ ![]() =tan∠EFD=tan30°=
=tan∠EFD=tan30°=![]() ,∴ PG=
,∴ PG=![]() FG=
FG=![]() ,∴
,∴ ![]() =
=![]() ,m=±2
,m=±2![]() .∴ P点坐标为(
.∴ P点坐标为(![]() ,2)或(-
,2)或(-![]() ,2).
,2).
21.原式=![]() -1+1-2·
-1+1-2·![]() =
=![]() -
-![]() =0.
=0.
22.原式=2×![]() -2--
-2--![]() +(
+(![]() -1)=1-2-
-1)=1-2-![]() +
+![]() -1=-2.
-1=-2.
23.(1)设A点坐标为(x,y),且x<0,y>0,则 S△ABO=![]() ·BO·BA=
·BO·BA=![]() ·(-x)·y=
·(-x)·y=![]() .∴ xy=-3.
.∴ xy=-3.
又∵ y=![]() ,即 xy=k,∴ k=-3.
,即 xy=k,∴ k=-3.
∴ 所求的两个函数的解析式分别为y=-![]() ,y=-x+2.
,y=-x+2.
(2)由y=-x+2,令y=0,得.x=2.
∴ 直线y=-x+2与x轴的交点D的坐标为(2,0).
再由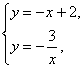 得
得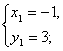
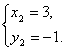
∴ 交点A为(-1,3),C为(3,-1).
∴ S△AOC=S△ODA+S△ODC=![]() ·DO·(y1+y2)=
·DO·(y1+y2)=![]() ×2×3(3+1)=4.
×2×3(3+1)=4.
24.(1)由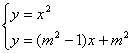 有x2-(m2-1)=0. ①
有x2-(m2-1)=0. ①
△=[-(m2-1)]2-4(-m2)=(m2+1)2>0.
∴ 无论m取任何实数,方程①总有两个不同的实数根,即无论m取任何实数,直线与抛物线总有两上不同的交点.
(2)解方程①,有x1=-1,x2=m2.令m2-(-1)=3.
∴ m=±2.
∴ m=±2时,直线与抛物线两交点的横坐标之差为3.
此时,y=x+2,A(-,1),B(2,4).由勾股定理,得OA=![]() ,OB=
,OB=![]() .
.
过B作x轴的垂线,交x轴于点M,过点A作BM的垂线,交BM于N,则AN=3,NB=3.∴ AB=![]() .∵ AO2+AB2=OB2,∴由勾股定理逆定理,知△AOB为直角三角形,且∠BAO=90°.设OB边上的高为h,则有
.∵ AO2+AB2=OB2,∴由勾股定理逆定理,知△AOB为直角三角形,且∠BAO=90°.设OB边上的高为h,则有![]() AB·OA=
AB·OA=![]() OB·h,即
OB·h,即![]() ·
·![]() =
=![]() ·h.
·h.
∴ h=![]() =
=![]() =
=![]() .
.
25.(1)∵ BC是半圆O的直径,OA是半径,且OA⊥BC,∴ ∠B=∠OAF=45°,OB=OA,又AE=CF,∴ BE=AF,∴ △BOE≌△AOF.
∴ S四边形AEOF=S△AOB=![]() OB·OA=
OB·OA=![]() r2.
r2.
(2)∵ BC是半圆的O的直径,∴ ∠EAF=90°且AC=AB=![]() r2.
r2.
∵ y=S△OEF=S四边形AEOF-S△AEF=![]() r2-
r2-![]() AE·AF F=
AE·AF F=![]() r2-
r2-![]() x(
x(![]() r-x),
r-x),
∴ y=![]() x2-
x2-![]() rx+
rx+![]() r2(0<x<
r2(0<x<![]() r).
r).
(3)当S△OEF=![]() S△ABC时,即y=
S△ABC时,即y=![]() (
(![]() ·2r·r)=
·2r·r)=![]() r2.∴
r2.∴ ![]() x2--
x2--![]() rx+
rx+![]() r2=
r2=![]() r2.
r2.
即![]() x2-
x2-![]() rx+
rx+![]() r2=0.解这个方程,得x1=
r2=0.解这个方程,得x1=![]() r,x2=
r,x2=![]() r.
r.
∴ 当S△OEF=![]() S△ABC时,
S△ABC时,![]() =
=![]() ,
,![]() =
=![]() ;或者
;或者![]() =
=![]() ,
,![]() =
=![]() .
.
当AE=![]() r时,AF=
r时,AF=![]() r,EF=
r,EF=![]() =
=![]() =
=![]() r;当AE=
r;当AE=![]() r时,AF=
r时,AF=![]() r,EF=
r,EF=![]() r.
r.
26.由题意,得PB+PC=m-2,PB·PC=m+2.由BC=PC-PB=4,得(PC-PB)2=16,即(PC+PB)2-4PC·PB=16.
∴ (m-2)2-4(m+2)=16.解得m=10,或m=-2.
∵ 当m=-2时,PB+PC<0,∴ m=-2不合题意,舍去.∴ m的值为10.又由题意,得PA2=PB·PC=12,∴ PA=2![]() .
.
27.sin60°-![]() -(
-(![]() )-1=
)-1=![]() -
-![]() -
-![]() -2=-2
-2=-2
28.(1)令y=0,则-ax2+ax+6a=0,即-a(x-3)(x+2)=0,
∵ a≠0,∴ x1=3,x2=-2,∴ A(-2,0),B(3,0).
(2)作CD⊥AB于E,分别把x=0,x=1代入y=-ax2+ax +6a
∴ DC=1且DC∥x轴,而AB=5,∴ DC≠AB,∴ 四边形ABCD为梯形,
∵ CE⊥AB,C(1,6a),∴ E(1,0),CE=OD=6a.∴ BE=OA=2.
证得△AOD≌△BEC,∴ AD=BC,∴ 四边形ABCD为等腰梯形.
(3)连结BD,证得∠CAB=∠DBA,
∵ ∠CAB=∠ADO,∴ ∠ADO=∠DBA,∴ △ADO∽△DOB,
∴ ![]() =
=![]() ,∴
,∴ ![]() =
=![]() ,解得a=
,解得a=![]() (舍负)
(舍负)
29.(1)由题意⊙O的半径OA=1,OB=2,由切割线定理:CF2=CO·CB,即(2![]() )2=CO(CO+2),
)2=CO(CO+2),
(2)连结OF,由题意:OE是⊙O的切线,∴ OE=EF,∠OEA=∠FEA,∴AE⊥OF,而OB的中点,∴ BF⊥OF,∴ AE∥BF.
(2)解:由(2)得,AE∥BF.∴ ![]() ,∴
,∴ ![]() ,∴ FE
,∴ FE![]() 而AE∥BF,点A是OB的中点,∴ 点E是OD的中点,∴ OD=2OE=2EF=
而AE∥BF,点A是OB的中点,∴ 点E是OD的中点,∴ OD=2OE=2EF=![]() ,∴点D的坐标为(0,
,∴点D的坐标为(0,![]() )设直线BD的解析式为y=kx+b,把点B(-2,0),D(0,
)设直线BD的解析式为y=kx+b,把点B(-2,0),D(0,![]() )代入得
)代入得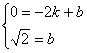 解之k
解之k![]() ,∴ 直线BD的解析式为
,∴ 直线BD的解析式为![]() .
.
30.∵a是锐角,∴ tana·cota=1∴ ![]() ,∴
,∴ ![]()
又∵ tana>0,cota>0, ∴ tana+cota=k>o, ∴ k=3
此时,△=![]() >0,经检验,k的值为3.
>0,经检验,k的值为3.
31.(1)∵ BO⊥PO,PC⊥PB,∵ ∠1=∠2,∵A(4,0)),C(4,y)在l上,∵ ∠BOP=∠PAC=![]() ,∴ △BOP∽△PAC,∴
,∴ △BOP∽△PAC,∴ ![]() ,∴
,∴ ![]() =
=![]() .∵ x<0,y<0,∴
.∵ x<0,y<0,∴ ![]() =
=![]() ,∴ y=
,∴ y=![]() x2+x.
x2+x.
(2)∵ x<0,且x取最大整数,∴ x=-1.此时y=![]() ×C-D2-1=
×C-D2-1=![]() ,∵ BO∥l,∴ △BOQ∽△CAQ,∴
,∵ BO∥l,∴ △BOQ∽△CAQ,∴ ![]() ,设Q点坐标为[a,0],则
,设Q点坐标为[a,0],则![]() =
=![]() ,5a=16(4-a)∴a=
,5a=16(4-a)∴a=![]() ,∴ Q点的坐标为(
,∴ Q点的坐标为(![]() ,0).
,0).
32.(1)∵ ∠B=90°,OP⊥AB,∴ ∠AOP=∠B=90°,∴ △AOP∽△ABC.∴ ![]() .
.
∴ AB=4,BC=3,O是AB的中点,∴ ![]() =
=![]() .
.
∴ OP=![]() ∵
∵ ![]() =OP<AO=OB=2,
=OP<AO=OB=2,![]() +2>2,∴ OP+AO>OB.即AO、OB、OP中,任意两条线段的长度之长大于第三条线段的长度.另解:∵ ∠B=90°,OP⊥AB.∴ OP∥BC.又∵ O是AB的中点,∴ OP是△ABC的中位线.∴ OP=
+2>2,∴ OP+AO>OB.即AO、OB、OP中,任意两条线段的长度之长大于第三条线段的长度.另解:∵ ∠B=90°,OP⊥AB.∴ OP∥BC.又∵ O是AB的中点,∴ OP是△ABC的中位线.∴ OP=![]() BC.∵ BC=3,∴ OP=
BC.∵ BC=3,∴ OP=![]()
(2)当M在OB上时,设AM=x(2≤x≤4)则MB=4-x.∵ △AMN∽△ABC,∴ ![]() .∴ MN=
.∴ MN=![]() =
=![]() x.
x.
又MN<AM,MB<AM.
依题意,得:MN+MB>AM,∴ ![]() x+(4-x)>x.
x+(4-x)>x.
解之得,x<![]() ,∴ AM的取值范围为2≤AM<
,∴ AM的取值范围为2≤AM<![]() .
.