三角形期末综合测试
【同步达纲练习】
一、选择(3分×9=27分)
1.△ABC中，AB=AC=4，BC=a,则a的取值范围是( )
A.a＞0 B.0＜a＜4 C.4＜a＜8 D.0＜a＜8
2.两个三角形，具备下列条件之一：①两角及一个角的对边对应相等 ②两边及其中一边的对角对应相等，能判定这两个三角形全等的( )
A.只有① B.只有② C.①②都行 D.①②都不能
3.在△ABC和△A′B′C′中∠C=∠C′=90°,下列条件①AC=A′C′②BC=B′C′③AB=A′B′，AC=A′C′中，能判定△ABC≌△A′B′C′的有( )
A.0个 B.1个 C.2个 D.3个
4.△ABC中，CA=CB，D为BA中点，P为直线CD上的任一点，那么PA与PB的大小关系是( )
A.PA＞PB B.PA＜PB C.PA=PB D.不能确定
5.P为∠MON内一点，PA⊥OM于OA，PB⊥ON于B，下列命题.①若∠MOP=∠NOP，则PA=PB ②若PA=PB，则∠MOP=∠NOP，则( )
A.只有①正确 B.只有②正确 C.①②都正确 D.①②都不正确
6．△ABC和△A′B′C′中，已知∠A=∠B′, ∠C=∠A′,增加下列条件之一，仍不能判定△ABC和△A′B′C′全等的是( )
A.AC=B′A′ B.AB=A′B′ C.AB=B′C′ D.BC=C′A′
7.△ABC中，AB=13，BC=10，BC边上中线AP=12，则AB，AC关系为( )
A.AB＞AC B.AB=AC C.AB＜AC D.无法确定
8.四边形ABCD中，AB⊥BC ,AB=3,BC=4,CD=12,AD=13,则四边形面积为( )
A.32 B.36 C.39 D.42
9.等边△DCE中，以CD、ED向外作正方形ABCD，DEFG，则∠ADG度数( )
A.90° B.105° C.120° D.135°
二、填空(3分×10=30分)
1.△ABC中，∠A-∠B=10°,2∠C-3∠B=25°,则∠A= .
2.等腰三角形周长为21cm,一中线将周长分成的两部分差为3cm,则这个三角形三边长为________.
3.点A、B关于直线l对称，点C、D也关于l对称，AC、BD交于O，则O点在 上.
4.△ABC周长为36，AB=AC,AD⊥BC于D，△ABD周长为30cm,则AD= .
5.等腰三角形一腰上的高与另一腰夹角为45°,则顶角为 .
6.等边三角形面积为
a，则边长为 .
7.四边形ABCD中，AB⊥BC,AB=CD=2,BC=1,AD=3,则四边形ABCD面积为 .
8.a、b、c为△ABC三边的长，且a4+b4+
c4=a2c2+b2c2,则△ABC的形状是 .
9.三角形三边的长为15、20、25，则三条高的比为 .
10.CD为Rt△ABC的斜边上的高，AB=25，CD=12，则BC= .
三、解答题(40分)
1.△ABC中AB=AC，D在AC上，且AD=BD=BC.求△ABC的三内角度数.(6分)
2.如图末2，AC=BD，AD⊥AC，BD⊥BC，求证AD=BC.(6分)
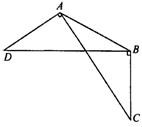
图末2
3.CD为Rt△ABC斜边的中线 V，DE⊥AC于E，BC=1，AC=.求△CED的周长.(7分)
4. 如图末3，AD为△ABC的中线，∠ADB的平分线交AB于E，∠ADC的平分线交AC于E,求证BE+CF＞EF.(9分)
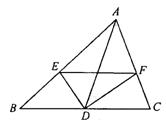
图末3
5.△ABC中，AD⊥BC交边BC于D.
(1)若∠A=90° 求证：AD+BC＞AB+AC (5分)
(2)若∠A＞90°,(1)中的结论仍然成立吗？若不成立，请举反例，若成立，请给出证明(7分)
参考答案
【同步达纲练习】
一、D A D C C B B B C
二、1.55° 2.(8,8,5)或(6,6,9) 3.l 4.12 5.45°或135° 6.2a 7.
+1 8.等腰直角三角形 9.20∶15∶12 10.15或20.
三、1.设∠A=x AD=DB=BC AB=AC ∴∠ABD=x ∠BDC=2x ∠ABC=∠C=2x ∠DBC=x ∴5x=180° x=36° ∴∠A=36°
∠C=72° ∠ABC=72°
2.连DC，∠DAC=∠DBC=90° AC=BD DC=DC
∴Rt△DAC≌△CBD (HL) ∴AD=BC.
3.∵∠ACB=90° BC=1 AC= ∴AB=2 ∠A=∠ACD=30°
CD=1 DE= CE=
周长为
4.延长ED至G，使ED=DG，连GC，GF DE平分∠BDA，DF平分∠ADC
∴∠EDF=90°,ED=DG ∴EF=FG，△BED≌△CGD ∴BE=GC
GC+CF＞GF.∴BE+CF＞EF.
5.(1)∵∠A=90° ∴AB2+AC2=BC2 AB·AC=AD·BC.
(AB+AC)2=AB2+AC2+2AB·AC=BC2+2AD·BC＜BC2+2AD·BC+AD2=(BC+AD)2
∴AD+BC＞AB+AC.
(2)若∠A＞90°,上述结论仍成立.
证∵∠A＞90°,作AE⊥AB交BC于E，则AD为Rt△BAE斜边上的高 由(1)
∴AD+BE＞AB+AE① 在△AEC中 AE+EC＞AC②
①+② AD+BE+EC+AE＞AB+AC+AE ∴AD+BC＞AB+AC