初三数学试卷

初三数学试卷　　　　　　　 姓名　　　　  1/21

一、填空（30分）

1、　　　　　　  ， 的倒数　　　　　　　  ，  　　　　　　  ，

2、方程的根　　　　　　　　  ， 方程的根　　　　 　　　　 ，

3、的自变量的取值范围　　　　　　　　　　　　  ,

4、⊙O半径为1，点P到O的距离为2，过点P引⊙O的切线，那么切线长为 　　　　　 ，

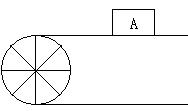
5、如图半径为30cm的转动轮转过240⁰角时，传送带上的物体A平移的距离为 　　　　　　，

6、抛物线与x轴的交点坐标是　　　　　  ，与y轴的交点坐标 　　　；当x　　　 时，y随x的增大而减小；若将抛物线沿x轴翻折，得到新抛物线的解析式　　　　　　　　　　 

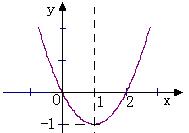7、二次函数的图象如图所示，

（1）　　　 二次函数的解析式　　　　　　　　

（2）　　　 当x 　　　　　时， y=3

（3）　　　 当x 　　　　　时， y>0

8、关于x的方程有实数根，则m的取值范围 　　　　　　　　　 ,

9、=　　　　　　　  ,　　若=0，则锐角α=　　　　  ,

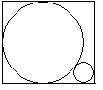
10、两圆有多种位置关系，图中不存在位置关系是　　　　　　　　　 ,

11、为某一住宅区的平面示意图，其周长800m,为了美化环境，计划在住宅周围5 m，（外）作绿化带，则此绿化带的面积　　　　　　　　　　　 ,

 

 

 

 

 

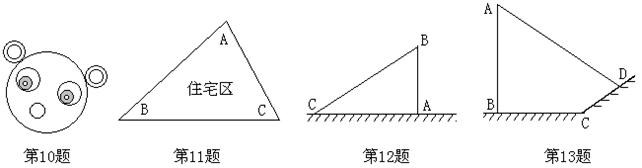
12、如图一棵大树被风折断，树顶落在地面C处，且与地面成30⁰的角，AC=6m，则原来树高　　　 ,

13、如图电线杆AB的影子恰好落在土坡的坡面CD和地面BC上，且CD=4m，BC=10m，CD与地面成30⁰角，且此时测得1m杆的影子长为2m，则电线杆的高度为　　　　　　　　　　  m

14、要用一个矩形纸片上画出半径为4cm和1cm的两个外切圆，该矩形面积的最小值是　　　　　 ,

15、按一定规律排列一列数依次：，，，，，……　

按次规律下去，这列数中的第7个数是　　　　　　　　　　  ,

二、选择(20分)

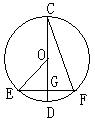
1、⊙O的直径CD过弦EF的中点G，∠EOD=40⁰,则∠DCF为(　　)

A　80⁰　　　　  B　50⁰ 　　　C　40⁰　　　　 D　20⁰

2、现有A、B两枚均匀的小立方体，每个面上分别标有1、2、3、4、5、6，用小莉掷A立方体朝上的数字为x，小明掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在抛物线上的概率为――――――――――――――――――――― ――――――(　　)

A　　 　　　　　　 B　 C　　 　　　　　　　　D　

3、平面直角坐标系中，P（x－2，x）在第二象限，则x的取值范围―――――――――――――(　　)

A　  0<x<2　　　　　  B　x<2  C　　 x>0　　　　　　　  D　 x>2

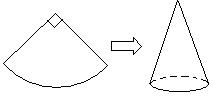4、现有一圆心角90⁰，半径为8cm的扇形纸片，

用它恰好围成一个圆锥的侧面（接缝忽略不计），

则该圆锥的底面圆的半径为――――(　　)　　　　　　　　　　　　　　 

A　 4 cm　　　B　 3 cm C　 2 cm　　　 D　 1 cm

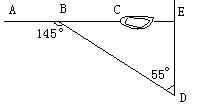5、如图沿AC方向开山修路，为加快施工进度，要在小山的另一边

同时施工。现在AC上取一点B，使∠ABD=145⁰，BD=500m，

∠D=55⁰，要使A、C、E成一直线，那么开挖点E离点D的距离(　　)

  A　500·sin55⁰m　　　　　　　 B　500·cos55⁰m  

 C　500·tan55⁰m　　　　　　　 D　 

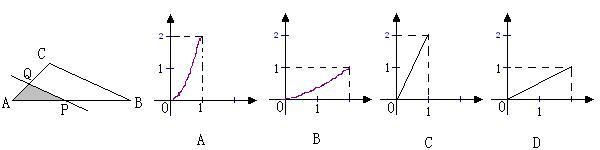
6、的边长AB＝2，面积为1，直线PQ∥BC，分别交AB、AC于P、Q，设AP=t，面积为S，则S关于t的函数图象大致是―――――――――――――――――――――――――――――(　　)

7、 抛物线不动，把x、y轴分别向上、向右平移2个单位长度，则新坐标系下抛物线的解析式(　　)

A　　 B　 C  　　D　

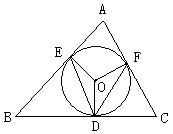
8、⊙O内切于，切点为D、E、F，∠B=50⁰, ∠C=60⁰,连结OE、OF、DE、DF，则∠FDE度数(　　)

A　45⁰　　　　　　　  B　55⁰  C　65⁰　　　　　　　　 D　70⁰

9、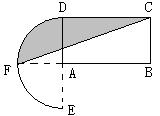如图是一个商标图案，已知矩形ABCD

中，AB＝8，且圆弧的圆心为A，半径为4，

则商标图案面积为――――――(　　)

A　 4π+8　　　　　　  B　 4π+16　　　

C　 3π+8　　　　　　  D　 3π+16

10、在平面直角坐标系内，直线与两坐标轴交于A、B两点，点O为坐标原点，若在该坐标平面内有点P（不与点A、B、O重合）为顶点的直角三角形与全等，且这个以点P为顶点的直角三角形与有一条公共边，则所有符合条件的P点个数为―――――――――――――(　　)

  A　9个　　　　　　　  B　 7个　　　　　　  C　 5个　　　　　　　　 D　 3个

三、计算、方程（20分）

1、·　　　　  2、

3、　　　　　　　　　  4、

四、解答题（6分+8分+5分+10分+11分+10分）

1、  口袋中有5张完全相同的卡片，分别协有1cm、2cm、3cm、4cm、5cm，口袋外有2张卡片，分别写有4cm、和5cm。现随机从袋中取出一张卡片，与口袋外两张卡片放在一起，以卡片上的数量分别作为三条线段的长度，回答下列问题：

（1） 求这三条线段能构成三角形的概率；

（2） 求这三条线段能构成直角三角形的概率；

（3） 求这三条线段能构成等腰三角形的概率；

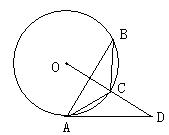2、如图，内接与⊙O，点D在OC的延长线上，sinB＝0.5，

∠CAD=30⁰,

（1）求证：AD是⊙O的切线

（2）若OD⊥AB，BC=5，求AD的长

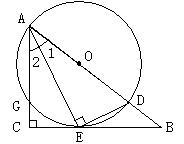
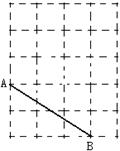3、如图，A、B是4×5网络中的格点，网络的每个小正方形的边长为1，

若设A坐标（0，2），B坐标（3，0），请在图上清晰标出使以A、B、C

为顶点的三角形是等腰三角形的所有格点C的位置并写出坐标

4、如图，已知在Rt中，∠C＝90⁰，AE平分∠BAC交BC于点E，

点D在AB上，DE⊥AE，⊙O是Rt的外接圆，交AC于点G。

（1）　　　 判断BC与⊙O的位置关系，并说明理由；

（2）　　　 若AC+GC=5，求直径AD的值。

5、某校九年级（1）班共有50人，据统计原来每人每年用于购买饮料的平均支出a元。经测算和市场调查，若该班级集体改饮某品牌的纯净水，则年总量费用由两部分组成：一部分是购买纯净水的费用，另一部分是其他费用780元，其中，纯净水的售价x（元/桶）与年购买总量y之间满足如图所示关系

（1） 求y与x的函数关系式

（2） 若该班级每年需要纯净水380桶，且a为120时，请你根据提供的信息分析一下：该班学生集体该学生集体改饮桶装纯净水与个人买饮料，哪一种花钱少？

(3)当x至少为多少时，该班级集体改饮桶装纯净水一定合算？从计算结果看，你有何感想（不超过30字）

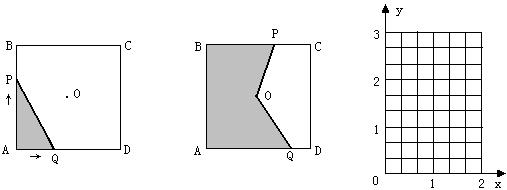
6、如图，正方形ABCD的边长为2 cm，在对称中心O处有一钉子。动点P、Q同时从点A出发，点P沿A→B→C方向以每秒2 cm的速度运动，到点C停止，点Q沿A→D方向以每秒1 cm的速度运动，到点D停止。P、Q两点用一条可伸缩的细橡皮筋联结，设x秒后橡皮筋扫过的面积为y cm²，

(1)　  当0≤x≤1时，求y与x之间的函数关系式；

(2)　  当橡皮筋刚好触及钉子时，求x值

(3)　  当1≤x≤2时，求y与x之间函数关系式，并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围；

(4)　  当0≤x≤2时，请在给出的直角坐标系中画出y与x之间的函数图象。