代 数 与 几 何 综 合 题
 1、如图,
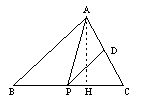
1、如图,![]() 中,BC=4,
中,BC=4,![]() ,P为BC上一点,过点P作PD//AB,交AC于D。连结AP,问点P在BC上何处时,
,P为BC上一点,过点P作PD//AB,交AC于D。连结AP,问点P在BC上何处时,![]() 面积最大?
面积最大?
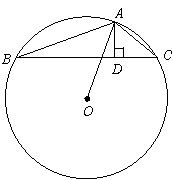
2.在钝角△ABC 中,AD⊥BC,垂足为D点,且AD与DC的长度为x2-7x+12=0方程的两个根,⊙O是△ABC的外接圆,如果BD长为a(a>0). 求△ABC的外接圆⊙O的面积.
 |
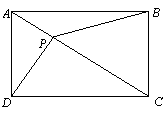
3.如图,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.
(1)写出y与x的函数关系,并确定自变量x的范围.
(2)有人提出一个判断:“关于动点P,⊿PBC面积与⊿PAD面积之和为常数”.请你说明此判断是否正确,并说明理由.
4.如图,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M,此时
(1)设矩形EFGH的长HG=y,宽HE=x,确定y与x的函数关系式;
(2)当x为何值时,矩形EFGH的面积S最大?
(3)以面积最大的矩形EFGH为侧面,围成一个圆柱形的铁桶,怎样围时,才能使铁桶的体积较大?请说明理由(注:围铁桶侧面时,接缝无重叠,底面另用材料配备).

5.如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 厘米,质点P从A点出发沿线路
厘米,质点P从A点出发沿线路![]() 作匀速运动,质点Q从AC的中点D同时出发沿线路
作匀速运动,质点Q从AC的中点D同时出发沿线路![]() 作匀速运动逐步靠近质点P,设两质点P、Q的速度分别为1厘米/秒、
作匀速运动逐步靠近质点P,设两质点P、Q的速度分别为1厘米/秒、![]() 厘米/秒(
厘米/秒(![]() ),它们在
),它们在![]() 秒后于BC边上的某一点E相遇。
(1)求出AC与BC的长度;
秒后于BC边上的某一点E相遇。
(1)求出AC与BC的长度;
(2)试问两质点相遇时所在的E点会是BC的中点吗?为什么?
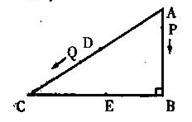 (3)若以D、E、C为顶点的三角形与△ABC相似,试分别求出
(3)若以D、E、C为顶点的三角形与△ABC相似,试分别求出![]() 与
与![]() 的值;
的值;

6.如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(3,0),(3,4)。动点M、N分别从O、B同时出发,以每秒1个单位的速度运动。其中,点M沿OA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥AC,交AC于P,连结MP。已知动点运动了x秒。
(1)P点的坐标为( , );(用含x的代数式表示)
(2)试求 ⊿MPA面积的最大值,并求此时x的值。
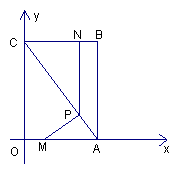 (3)请你探索:当x为何值时,⊿MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果
(3)请你探索:当x为何值时,⊿MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果
7、如图,把矩形OABC放置在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得到折痕EF。
(1) 可以通过________办法,使四边形AEFO变到四边形BEFC的位置(填“平移”、“旋转”或“翻转”);
(2)
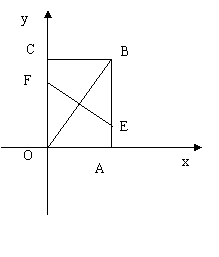 求点E的坐标;
求点E的坐标;
(3) 若直线l把矩形OABC的面积分成相等的两部分,
则直线l必经过点的坐标是______.
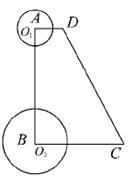 8.如图,已知直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60o,AD =3cm,BC
=9cm.⊙O1的圆心O1从点A开始沿A—D—C折线以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以
8.如图,已知直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60o,AD =3cm,BC
=9cm.⊙O1的圆心O1从点A开始沿A—D—C折线以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以![]() cm/s的速度向点A运动,如果⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts
cm/s的速度向点A运动,如果⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts
(1)请求出⊙O2与腰CD相切时t的值;
(2)在0s<t≤3s范围内,当t为何值时,⊙O1与⊙O2外切?
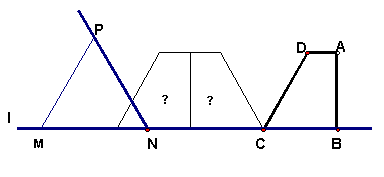
9、已知:如图,在直角梯形ABCD中,AD∥BC,BC=5cm,CD=6cm,∠DCB=60°,∠ABC=90°。等边三角形MPN(N为不动点)的边长为![]() cm,边MN和直角梯形ABCD的底边BC都在直线
cm,边MN和直角梯形ABCD的底边BC都在直线![]() 上,NC=8cm。将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得图形②,如此翻折下去。
上,NC=8cm。将直角梯形ABCD向左翻折180°,翻折一次得到图形①,翻折二次得图形②,如此翻折下去。
(1)将直角梯形ABCD向左翻折二次,如果此时等边三角形的边长a≥2cm,这时两图形重叠部分的面积是多少?
(2)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形ABCD的面积,这时等边三角形的边长a至少应为多少?
(3)将直角梯形ABCD向左翻折三次,如果第三次翻折得到的直角梯形与等边三角形重叠部分的面积等于直角梯形面积的一半,这时等边三角形的边长应为多少?