第3课 整式
知识点
代数式、代数式的值、整式、同类项、合并同类项、去括号与去括号法则、幂的运算法则、整式的加减乘除乘方运算法则、乘法公式、正整数指数幂、零指数幂、负整数指数幂。
大纲要求
1、 了解代数式的概念,会列简单的代数式。理解代数式的值的概念,能正确地求出代数式的值;
2、 理解整式、单项式、多项式的概念,会把多项式按字母的降幂(或升幂)排列,理解同类项的概念,会合并同类项;
3、 掌握同底数幂的乘法和除法、幂的乘方和积的乘方运算法则,并能熟练地进行数字指数幂的运算;
4、 能熟练地运用乘法公式(平方差公式,完全平方公式及(x+a)(x+b)=x2+(a+b)x+ab)进行运算;
5、 掌握整式的加减乘除乘方运算,会进行整式的加减乘除乘方的简单混合运算。
考查重点
1.代数式的有关概念.
(1)代数式:代数式是由运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子.单独的一个数或者一个字母也是代数式.
(2)代数式的值;用数值代替代数式里的字母,计算后所得的结果p叫做代数式的值.
求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.
(3)代数式的分类
2.整式的有关概念
(1)单项式:只含有数与字母的积的代数式叫做单项式.
对于给出的单项式,要注意分析它的系数是什么,含有哪些字母,各个字母的指数分别是什么。
(2)多项式:几个单项式的和,叫做多项式
对于给出的多项式,要注意分析它是几次几项式,各项是什么,对各项再像分析单项式那样来分析
(3)多项式的降幂排列与升幂排列
把一个多项式技某一个字母的指数从大列小的顺序排列起来,叫做把这个多项式按这个字母降幂排列
把—个多项式按某一个字母的指数从小到大的顺斤排列起来,叫做把这个多项式技这个字母升幂排列,
给出一个多项式,要会根据要求对它进行降幂排列或升幂排列.
(4)同类项
所含字母相同,并且相同字母的指数也分别相同的项,叫做同类顷.
要会判断给出的项是否同类项,知道同类项可以合并.即![]() 其中的X可以代表单项式中的字母部分,代表其他式子。
其中的X可以代表单项式中的字母部分,代表其他式子。
3.整式的运算
(1)整式的加减:几个整式相加减,通常用括号把每一个整式括起来,再用加减号连接.整式加减的一般步骤是:
(i)如果遇到括号.按去括号法则先去括号:括号前是“十”号,把括号和它前面的“+”号去掉。括号里各项都不变符号,括号前是“一”号,把括号和它前面的“一”号去掉.括号里各项都改变符号.
(ii)合并同类项: 同类项的系数相加,所得的结果作为系数.字母和字母的指数不变.
(2)整式的乘除:单项式相乘(除),把它们的系数、相同字母分别相乘(除),对于只在一个单项式(被除式)里含有的字母,则连同它的指数作为积(商)的一个因式相同字母相乘(除)要用到同底数幂的运算性质:
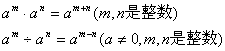
多项式乘(除)以单项式,先把这个多项式的每一项乘(除)以这个单项式,再把所得的积(商)相加.
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加.
遇到特殊形式的多项式乘法,还可以直接算:
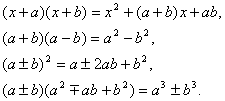
(3)整式的乘方
单项式乘方,把系数乘方,作为结果的系数,再把乘方的次数与字母的指数分别相乘所得的幂作为结果的因式。
单项式的乘方要用到幂的乘方性质与积的乘方性质:
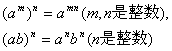
多项式的乘方只涉及
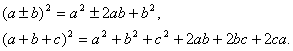
考查重点与常见题型
1、 考查列代数式的能力。题型多为选择题,如:
下列各题中,所列代数错误的是( )
(A) 表示“比a与b的积的2倍小5的数”的代数式是2ab-5
(B) 表示“a与b的平方差的倒数”的代数式是
(C) 表示“被5除商是a,余数是2的数”的代数式是5a+2
(D) 表示“数的一半与数的3倍的差”的代数式是-3b
2、 考查整数指数幂的运算、零指数。题型多为选择题,在实数运算中也有出现,如:
下列各式中,正确的是( )
(A)a3+a3=a6 (B)(3a3)2=6a6 (C)a3•a3=a6 (D)(a3)2=a6
整式的运算,题型多样,常见的填空、选择、化简等都有。
考查题型:
1.下列各题中,所列代数错误的是( )
(E) 表示“比a与b的积的2倍小5的数”的代数式是2ab-5
(F) 表示“a与b的平方差的倒数”的代数式是
(G) 表示“被5除商是a,余数是2的数”的代数式是5a+2
(H) 表示“数a的一半与数b的3倍的差”的代数式是-3b
2.下列各式中,正确的是( )
(A)a3+a3=a6 (B)(3a3)2=6a6 (C)a3•a3=a6 (D)(a3)2=a6
3.用代数式表示:(1)a的绝对值的相反数与b的和的倒数;
(2)x平方与y的和的平方减去x平方与y的立方的差;
4.-的系数是 ,是 次单项式;
5.多项式3x2-1-6x5-4x3是 次 项式,其中最高次项是 ,常数项是 ,三次项系数是 ,按x的降幂排列 ;
6.如果3m7xny+7和-4m2-4yn2x是同类项,则x= ,y= ;这两个单项式的积是__。
7.下列运算结果正确的是( )
①2x3-x2=x ②x3•(x5)2=x13 ③(-x)6÷(-x)3=x3 ④(0.1)-2•10-1=10
(A)①② (B)②④ (C)②③ (D)②③④
考查训练:
1、代数式a2-1,0,,x+,-,m,,–3b中单项式是 ,多项式是 ,分式是 。
2、-是 次单项式,它的系数是 。
3、多项式3yx2-1-6y2x5-4yx3是 次 项式,其中最高次项是 ,常数项是 ,三次项系数是 ,按x的降幂排列为 。
4、已知梯形的上底为4a-3b,下底为2a+b,高为3a+b。试用含a,b的代数式表示出梯形的面积,并求出当a=5,b=3时梯形的面积。
5、下列计算中错误的是( )
(A)(-a3b)2·(-ab2)3=-a9b8 (B) (-a2b3)3÷(-ab2)3=a3b3
(C)(-a3)2·(-b2)3=a6b6 (D)[(-a3)2·(-b2)3]3=-a18b18
6、计算:3xy3·(-x3y4)÷(-x2y3)2
7.已知代数式3y2-2y+6的值为8,求代数式y2-y+1的值
8.设a-b=-2,求-ab的值。
7、利用公式计算:
(1) (a2-b)( -b-a2) (2) (a-)2 (a2+)2(a+)2
(3)(x+y-z)(x-y+z)-(x+y+z)(x-y-z) (4)[(x2+6x+9) ÷(x+3)](x2-3x+9)
(5)(a2-4)(a2-2a+4)(a2+2a+4) (6)101×99
解题指导:
1、代数式是( )
(A)整式 (B)分式 (C)单项式 (D)无理式
2、如果3x7-myn+3和-4x1-4my2n是同类项,那么m,n的值是( )
(A)m=-3,n=2 (B) m=2,n=-3 (C) m=-2,n=3 (D) m=3,n=-2
3、正确叙述代数式(2a-b2)的是( )
(A) a与2的积减去b平方与3的商
(B)a与2的积减去b的平方的差除以3
(C)a与2倍减去b平方的差的(D)a的2倍减去b平方
4、用乘法公式计算:
(1) (-2a-3b)2 (2) (a-3b+2c)2 (3) (2y-z)2[2y(z+2y)+z2]2
5、计算:
(1)(c-2b+3a)(2b+c-3a) (2)(a-b)(a+b)2-2ab(a2-b2)
6、用竖式计算: (5-4x3+5x2+2x4)÷(3+x2-2x)
7、已知6x3-9x2+mx+n能被6x2-x+4整除,求m,n的值,并写出被除式。
8、已知x+y=4,xy=3,求:3x2+3y2;(x-y)2
巩固提高
1、 若一个多项式加上2x2-x3-5-3x4得3x4-5x3-3,则这个多项式是 ;
2、 若3xn-(m-1)x+1为三次二项式,则m-n2的值为 ;
3、 用代数式表示,m,n两数的和除这两数的平方的差 ;
用语言叙述代数式 ;
4.若除式=x+2,商式=2x+1,余式=-5,则被除式= ;
5、当x=-2时,ax3+bx-7=5,则x=2时,ax3+bx-7= ;
a-b=-2,a-c=-3,则(b-c)2-3(b-c)+1=
6、如果(a+b-x)2的结果中不含的x一次项,那么a,b必满足( )
(A) a=b (B)a=0,b=0 (C)a=-b (D)以上都不对
7、-[a-(b-c)]去括号正确的是( )
(A) -a-b+c (B)-a+b-c (C)-a-b-c (D)-a+b+c
8、设P是关于x的五次多项式,Q是关于x的三次多项式,则( )
(A)P+Q是关于的八次多项式 (B)P-Q是关于的二次多项式
(C)P·Q是关于的八次多项式 (D)是关于的二次多项式
9.下列计算中正确的是( )
(A)xn+2÷xn+1=x2 (B)(xy)5÷xy3=(xy)2
(C)x10÷(x4÷x2)=x8 (D)(x4n÷x2n) ·x3n=x3n+2
10.若(am+1bn+2)(a2n-1b2m)=a5b3,则m+n的值为( )
(A)1 (B)2 (C)3 (D)-3
11、计算:
(1) (-2ax)2·(-x4y3z3) ÷(-a5xy2)
(2) (an+2+2an+1) ÷(-an-1)
(3) 5(m+n)(m-n)-2(m+n)2-3(m-n)2 (4)(a-b+c-d)(-a-b-c-d)
(5)(-x-y)2(x2-xy+y2)2 (6)15+2a-{9a-[a-9-(3-6a)]}
(7)(a2c-bc2)-(a-b+c)(a+b-c)
*(8)(a-b)(a+b)2-(a+b)(a-b)2+2b(a2+b2)