二次函数复习
1、二次函数解析式的三种形式：
⑴一般式：
，顶点坐标：
，
对称轴：直线
，
当x= 时，
=
。
⑵顶点式：
，顶点坐标：（ ， ）
对称轴：直线
，当x=
时，
= 。
⑶两根式：
，其中
是
=0的两个实数根，图象与x轴的两个交点坐标为（ ，
）和 （ ，
）。
练习：
1．二次函数
的一般式是
，二次项系数，一次项系数，常数项分别是
。
2、抛物线
的顶点坐标是
，对称轴是
，开口向_____。
3、抛物线
经过点（3，5），则
= ；
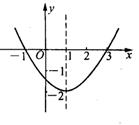
4、抛物线如图所示：当
=
时，
=0，当 时，
>0；当x
时，<0；
5、函数 y＝x2＋bx＋3 的图象经过点(－1, 0)，则 b＝ 。
6、二次函数 y＝(x－1)2＋2，∵a , ∴当 x＝ 时，y 有最 值是 。
7、函数 y＝
(x－1)2＋3，当 x
时，函数值 y 随 x 的增大而增大, 当 x
时，函数值 y 随 x 的增大而减小。
8、将 y＝x2－2x＋3 化成 y＝a (x－m)2＋k 的形式，则 y＝ 。
9、若点 A (2, m) 在函数 y＝x2－1 的图像上，则 A 点的坐标是 。
10、抛物线 y＝2x2＋3x－4 与 y 轴的交点坐标是 。
11、请写出一个二次函数以（2, 3）为顶点，且开口向上。 。
12、的图象
的图象
的图象
13、将抛物线 y＝2x2 向下平移 2 个单位，所得的抛物线的解析式为 。
14、把抛物线y=3x2先向上平移2个单位，再向右平移3个单位，所得抛物线的解析式是
15、把抛物线y＝
先向 平移 个单位，再向 平移 个单位的
。
三、二次函数y=ax2+bx+c(a≠0)的图象和性质
| 抛物线 | y=ax2+bx+c(a>0) | y=ax2+bx+c(a<0) |
| 顶点坐标 | ||
| 对称轴 | ||
| 位置 | ||
| 开口方向 | ||
| 增减性 | ||
| 最值 | ||
练习：
1、请研究二次函数
的图象和性质：
⑴开口方向： ；
⑵对称轴： ；
⑶顶点坐标： ；
⑷图象与x轴的交点坐标： __________;
⑸图象与y轴的交点坐标：
⑹图象与y轴的交点关于对称轴的对称点的坐标：
⑺用五点法画函数的草图:
⑻求这个函数的最值，当x= 时，
⑼当 时；y=0，当 时， y>0； 当 时，y<0。
⑽图象的平移： ;
⑾图象在x轴上截得的线段的长是： ;
⑿求图象与坐标轴交点所围成的三角形的面积： ;
⒀根据图像回答：当x 时，y随x的增大而增大，当x 时，y随x的增大而减小。
⒁求该函数关于x轴对称的函数解析式： ;
求该函数关于y轴对称的函数解析式： ;
求该函数关于原点对称的函数解析式： ;
求该函数绕顶点旋转180度的函数解析式： .
2、求满足下列条件的二次函数解析式：
⑴图象过（1，0）、（0，-2）和（2，3）。
⑵图象与x轴的交点的横坐标为-2和1，且过点（2，4）。
⑶当x=2时，y
=3，且过点（1，-3）。
3、已知抛物线y=x2+ax+a-2.
(1)证明:此抛物线与x轴总有两个不同的交点;
(2)求这两个交点间的距离(用关于a的表达式来表达);
(3)a取何值时,两点间的距离最小?
4、如图，二次函数的图象与
轴交于A、B两点，与
轴交于点C，点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．（1）求D点的坐标．（2）求一次函数的解析式．（3）根据图象写出使一次函数值大于二次函数的值的的取值范围．
