初三第三次月考数学试卷
考生注意：本卷共八大题，计23小题，满分150分，考试时间120分钟。
一、选择题（本题共10小题，每小题4分，共40分）。
每一个小题都给出代号为A、B、C、D的四个结论，其中只有一个是正确，把正确结论的代号写在题后的括号内。每一小题：选对得4分，不选、选错或选出的代号超过一个的（不论是否写在括号内）一律得0分。
1、函数y＝－中，自变量x 的取值范围是 
（ ）
A、x ≠－2 B、x ≤－2 C、x＝－2 D、x ≥－2且x ≠0
2、一种细菌的半径是4×10－5米，用小数表示为 （ ）
A、400000米 B、40000米 C、0.00004米 D、0.000004米
3、下列运算中，正确的是 （ ）
A、
＝±3 B、（a2）3＝a6 C、3 a·2
a＝6 a D、3－2＝－9
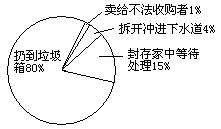4、把过期的药品随意丢弃，会造成对土
壤和水体的污染，危害人们的健康。如何
处理过期药品，有关机构随机对若干家庭
进行调查。调查结果绘制成如右的扇形统
计图，则对过期药品处理正确的家庭的扇
形的圆心角为 （ ）
A、54° B、72° C、288° D、342°
第4题图
5、如果一元二次方程k x2－4 x＋2＝0有实数根，那么k取值范围是（ ）
A、 k ≤2 B、k ≥2 C、k ＜2 D、k ≤2 且k≠0
6、下列语句正确的是 （ ）
A、三点确定一个圆 B、三角形的外心到三角形各边的距离相等
C、不是分式 D、三角形的内心不一定在三角形的内部
7、扇形的半径为30cm，圆心角为120°，用它做成一个圆锥的侧面，则
圆锥底面半径为 （ ）
A、10 cm B、20 cm C、10πcm D、20πcm
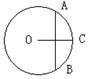8、如图，⊙O的直径为10 cm，弦AB垂直平分
半径OC，则弦AB长为 （ ）
A.2.5cm B.5 cm C.5cm D.10cm
9、某工厂一月份生产零件2万个，一季度共生产 第8题图
零件7.98万个，若每月的增长率相同，则每月的平均增长率为（ ）
A、约100% B、30% C、约15% D、10%
10、某种商品进价为800元，标价为1200元，由于商品积压，商店准备打折出售，但要保证利润率不低于5%，则至少打 （ ）。
A、6折 B、7折 C、7.5折 D、8折
二、填空题（本题共5小题，每小题5分，共25分）.
11、（－1）2＋（）－1－5÷（2.03－π）0的结果是___________.
12、已知3－是方程 x2＋m x＋7＝0的一个根，则m＝______，另一个根为________.
13、半径分别为4和5的相交两圆所成的公共弦长为6，则两圆的圆心距为________.
14、方程＋ ＝ 的解是__________.
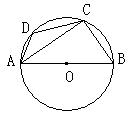
15、如图，已知AB⌒是⊙O的直径，C、D是⊙O上的两点，
且∠D＝130°，则∠BAC的度数为___________.
三、（本题共2小题，每小题8分，共16分）. 第15题图
16、解方程：3 x2＝x
17、先化简再求值：－·,其中x＝－1
四、（本题共2小题，每小题12分，共24分）
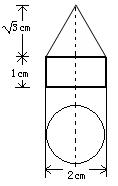
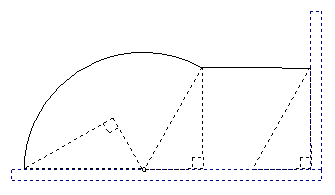
18、如图是某工件的二视图，按图中尺寸求工件的表面积。
19、如右图，P是⊙O的弦CB延长线上一点， 第18题图
点A在⊙O上，且∠PCA＝∠BAP.
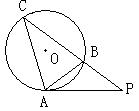（1）求证：PA是⊙O的切线。
（2）若PB:BC＝2:3且PC＝10,求PA的长。
第19题图
五、（本题满分12分）
20、阅读下面的材料，并解答后面的各题：
在形如ab＝N的式子中，我们已经研究过两种情况：
（1）已知a和b，求N，这是乘方运算；
（2）已知b和N，求a，这是开方运算。
现在，我们研究第三种情况：已知a和N，求b，我们把这种运算称为对数运算。
定义：如果ab＝N（a >0, a≠1, N>0）,则b叫做以a为底N的对数，记作b＝logaN.
例如，因为23＝8，所以log28＝3；因为2－3＝，所以log2＝－3.
（1）根据定义计算：①log381＝______；②log33＝______；③log41＝______；
④若logx16＝4,则；x＝________；
（2）设ax＝M, ay＝N,则logaM＝x，logaN＝y( a >0, a≠1,M,N均为正数) .
∵ax·ay＝ax＋y,∴ax＋y＝M·N. ∴loga(MN) ＝x＋y，即loga(MN) ＝logaM＋logaN.
这是对数运算的重要性质之一。进一步地，我们可以得出：
loga(M1 M2 M3…Mn) ＝_________________________________(其中M1 ,M2, M3,…,
Mn均为正数，a >0, a≠1)；loga＝______________（M,N均为正数，a >0, a≠1）。
六、（本题满分12分）
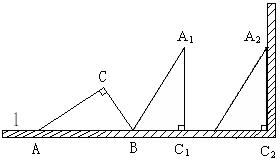
21、如图，在一个横截面为Rt△ABC的物体中，∠ACB＝90°,∠CAB＝30°,BC＝1米.工人师傅要把此物体搬到墙边，先将AB边放在地面（直线l）上,再按顺时针方向绕点B翻转到△A1BC1位置（BC1在l上）， 第21题图
最后沿BC1的方向平移到△A2B2C2的位置，其平移的距离为线段AC的长度（此时A2C2恰好靠在墙边）。
（1）请直接写出AB, AC的长；
（2）画出在搬动此物的整个过程A点所经过的路径，并求出该路径的长度。
七、（本题满分10分）
22、水果店花1500元进了一批水果，按50%的利润定价，无人购买。决定打折出售，但仍无人购买，结果又一次打折后才售完。经结算，这批水果共盈利500元。若两次打折相同，每次打了几折？（精确到0.1折）
八、（本题满分11分）
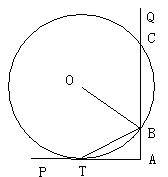
23、如图，∠PAQ是直角，⊙O与AP相切于点T，与AQ交于B、C两点。
（1）BT是否平分∠OBA?说明你的理由；
（2）若已知AT＝4，弦BC＝6，试求⊙O的半径R。
初三第三次月考数学试卷
参考答案
一、选择题:
1、A 2、C 3、B 4、A 5、D 6、C 7、A 8、C 9、B 10、B
二、填空题：
11、－2 12、－6，3＋ 13、4± 14、x＝2 15、40°
三、16、解：3 x2 －x＝0 ……………………3分
（3 x－1）x＝0 ……………………6分
3 x－1＝0或x＝0 ……………………7分
x1＝ x2＝0 ……………………8分
17、解：原式＝－· ………………2分
＝－ ………………5分
＝ ………………7分
当x＝－1时，原式＝ ＝1 …………………8分
四、18、解：由二视图得：圆柱的底面半径为r＝1cm,圆柱的高为h1＝1cm,
圆锥的底面半径r＝1cm，圆锥的高h2＝cm ………………3分
则圆柱的侧面积S圆柱侧＝2πrh1＝2π(cm2),
圆柱的底面积S＝πr2＝π（cm2） ………………6分
又圆锥的母线l＝＝＝2（cm）
∴圆锥的侧面积S圆锥侧＝πrl＝2π(cm2) ………………10分
∴此工件的表面积为S表＝S圆柱侧＋S圆锥侧＋S＝5π（cm2）…12分
19、证明：
（1）连结AO并延长交⊙O于D,连结BD
∵AD是⊙O的直径，∴∠ABD＝90°∴∠D＋∠DAB＝90°
又∵∠C＝∠D ,∠PCA＝∠BAP
∴∠BAP＋∠DAB＝90° ,∴PA是⊙O的切线。 …………6分
（2）∵∠PCA＝∠BAP,∠BPA＝∠APC
∴△ABP∽△CPA ∴AP2＝BP·PC
又∵PB:BC＝2:3 ,PC＝10 ,∴BP＝10×＝4
∴PA2＝4×10＝40 ∴PA＝2 …………………12分
五、20、（1）①4 ②1 ③0 ④2 ………………………………8分
（2）log a M1＋loga M2 ＋log a M3＋…＋loga Mn ……10分
log a M－loga N …………………………12分
六、21、（1）AB＝2米， AC＝米 …………………………………4分
（2）A点所经过的路径如右图。…8分
解：∠ACB＝90°, ∠CAB＝30°
∴由题图可知
∠A1BC1＝90°－30°＝60°
∴∠ABA1＝120°
∴⌒AA1＝＝ π
AA2＝
∴A点所经过的路径的长为
（ π＋）米。 ……12分
七、22、解：设每次打x折，由题意得
1500（1＋50%）（）2＝1500＋500 ……………………………………… 5分
解这个方程得，x2＝ ……………………………………… 8分
∴x1＝≈9.4 x2＝－（舍去） …………………………………… 9分
答：每次约打了9.4折。 ……………………………………………………10分
八、23、(1)BT平分∠OBA …………………2分
连结OT，因为⊙O与AP相切于点T,所以∠OTB＋∠BTA＝90°
又因为∠PAQ是直角，所以∠BTA＋∠ABT＝90°
又∠OTB＝∠OBT，所以∠OBT＝∠ABT，即BT平分∠OBA ……………6分
（2）
经O点作OD⊥BC交于D点，
则BD＝DC＝BC＝3,四边形OTAD是矩形，
所以OD＝AT＝4
在Rt△OBD中，OB＝ ＝＝5
所以⊙O的半径R等于5 …………………………………… 11分