初三第一学期数学期中测试
（满分120分，时间120分钟）
一. 选择题：（每题3分，共24分）
1. 下列说法错误的是：（ ）
A. 任何命题都有逆命题 B. 定理都有逆定理
C. 命题的逆命题不一定是正确的 D. 定理的逆定理一定是正确的
2. 在等边△ABC中,D为AC的中点,E为BC延长线上一点,且DB=DE,若△ABC的周长为12, 则△DCE的周长为（ ）
A. 4 B. 4+2
C. 4+ D. 4+2
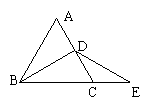
3. 下列结论错误的是（ ）
A. 到已知角两边距离相等的点在同一直线上
B. 一射线上有一点到已知角两边的距离相等这条射线平分已知角
C. 到角两边距离相等的一个点与这个角的顶点的连线不平分这个角
D. 角内有两点各自到角的两边的距离相等，经过这两点的直线平分这个角
4. 若一元二次方程(m-1)x2+3m2x+(m2+3m-4)=0有一根为零，则m=（ ）
A. 1 B. -4 C. 1或-4 D. -1或4
5. 当x为何值时，代数式x2－4x＋12的值与代数式－x2＋18的值相等（ ）
A. 
B. 
C. 
D. 
6. 如果平行四边形内一点P到平行四边形各边的距离相等，那么该四边形一定是（ ）
A. 矩形 B. 菱形 C. 正方形 D. 无法确定
7. 从菱形的一个钝角顶点向它的两条对边作垂线，这两条垂线分别垂直平分对边，则该菱形的钝角等于（ ）
A. 135° B. 150° C. 110° D. 120°
8. 下面哪个图能近似反映上午九点北京天安门广场上的旗杆与影子的位置关系（ ）
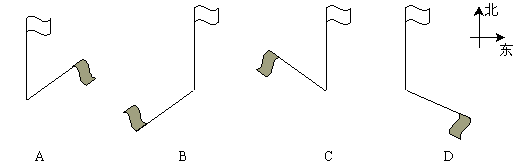
二. 填空题：（每题3分，共24分）
1. 命题“等腰三角形两底角平分线相等”的逆命题是 ；它是 命题（真、假）
2. 当m＝______时，关于x的方程(m+1)
+5+mx=0是一元二次方程。
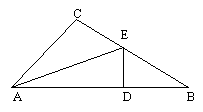
3. 如图，在△ABC中，∠C=90°，∠A的平分线交BC于E，DE⊥AB于D，BC=8，AC=6，AB=10，则△BDE的周长为_________。
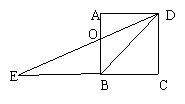
4. 正方形ABCD中（下图），若延长CB至E，使BD=BE，连接DE交AB于O,则∠DOB=__________度。
5. 已知：等腰梯形ABCD，AD∥BC，对角线AC⊥BD，AD=3cm，BC=5cm，则对角线AC=_________。
6. 已知直角三角形三边长为三个连续整数，则该三角形三边长分别为__________
7. 某工厂计划两年后产量翻番，则平均每月增长率是_______________
8. 有一块长方形的场地，长比宽多4米，周围有宽2米的道路环绕着，已知道路的面积与这块场地的面积相等，则场地的长与宽分别是 。
三. 作图题：（2×3=6）
1. 如图，在两条铁路之间有两个村庄A、B，现欲建一个中转站C，使得C到两条铁路的距离相等，且C到A、B两个村庄的距离也相等，试确定点C的位置。
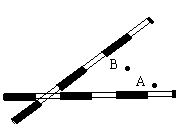
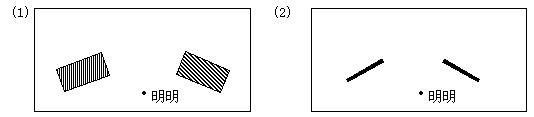
2. 明明与亮亮在借助两堵残墙玩捉迷藏游戏，若明明站在如图所示位置时，亮亮在哪个范围内活动是安全的？请在图(1)的俯视图(2)中画出亮亮的活动范围.
四. 用合适的方法解下列方程（每题4分）
1. 
（用公式法解）
2. 
（用配方法解）
3. 
（用因式分解法解）
4. 
五. 阅读理解：（6）
2600多年前，埃及有个国王想知道已经盖好的金字塔的确切高度，可是谁也不知道该怎样测量
人爬到塔顶上去吧，不可能.因为塔身是斜的，就是爬上去了，又用什么办法来测量呢？
后来，国王请到了一个名叫泰勒斯的学者来设法解决这个问题。泰勒斯选择了一个风和日丽的日子，在国王、祭司们的亲自驾临下，举行了测塔仪式
看热闹的人当然不少，人们拥挤着、议论着.看看时间已经不早，太阳光给每一位在场的人和巨大的金字塔都投下了长长的影子。当泰勒斯确知他自己的影子已等于他的身高时，他发出了测塔的命令。这时，助手们立即测出了金字塔的阴影的长度.接着，泰勒斯十分准确地算出了金字塔的高度。
（1）你知道泰勒斯这样做的道理吗？
（2）请你在泰勒斯的启示下，设计一个测量校园旗杆高度的方案。
六. 应用题：（8×2＝16）
1. 某农场要建一个长方形的养鸡场，鸡场的一边靠墙（墙长25m），另三边用木栏围成，木栏长40m。①鸡场的面积能达到180m2吗？能达到200m2吗？②鸡场的面积能达到250m2吗？如果能，请你给出设计方案；如果不能，请说明理由。
2. 某商场销售一批名牌衬衫，平均每天可售出20件,每件盈利40元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施,经调查发现如果每件衬衫每降价1元，商场平均每天可多售出2件。若商场平均每天要盈利1200元，每件衬衫应降价多少元?
七. 探索与证明（7×4=28）
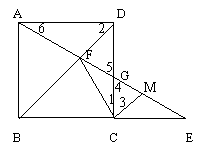
1. 已知：正方形ABCD，E为BC延长线上一点，AE交BD于F，交DC于G，M为GE中点,求证：CF⊥CM
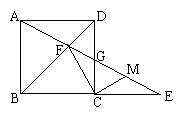
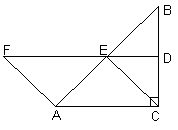
2. 如图，AD是△ABC的角平分线，AD的中垂线分别交AB、BC的延长线于点F、E
求证：(1) ∠EAD=∠EDA；(2) DF∥AC；(3) ∠EAC=∠B.
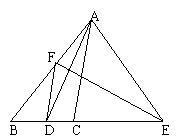
3. 如图，△ABC中，∠ACB=90°，D为AB中点，四边形BCED为平行四边形.，DE、AC相交于点F.求证：
（1）点F为AC中点；
（2）试确定四边形ADCE的形状，并说明理由；
（3）若四边形ADCE为正方形，△ABC应添加什么条件，并证明你的结论
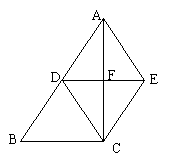
4. 如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF＝CE。
（1）求证：四边形ACEF是平行四边形；
（2）当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论；
（3）四边形ACEF有可能是正方形吗？为什么？
【试题答案】
一. 1. B 2. B 3. C 4. B 5. C 6. B
7. D 8. C
二. 1. 在三角形中，若两个角的角平分线相等，那么这个三角形是等腰三角形；真
2. 
3.
10 4.
112.5 5.
6. 3，4，5 7. 41％ 8. 12米，8米
三. 1. 作角的平分线，作AB的垂直平分线，交点为C
2. 略
四.
1. 
，
2. 
3. 
，
4. 
，
五. （1）同一时刻，阳光下泰勒斯的身高与其影长之比与金字塔的高度与其影长之比相等
（2）同一时刻，测量竹竿高度为a，影子为b，测旗竿的影子为c
设旗竿高度为d
六.
1. （1）解：设宽为x米，长
米
，能达到
能达到
（2）
所以不能
2. 解：设每件衬衫应降价x元
，
七. 略证：
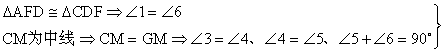
2. （1）略
（2）
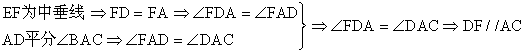
（3）
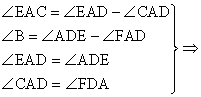结论
3. （1）
平行四边形DBEC
，D为AB中点
得到四边形ADCE为平行四边形，DE、AC交于F
F为AC中点
（2）菱形，DC＝AD
（3）
，
为等腰
（4）<1>证
<2>
<3>不可能