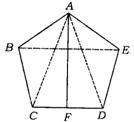
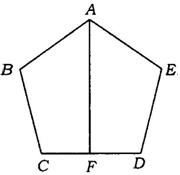
中考数学真题演练8 1．（温州市）已知：菱形ABCD中（如图），∠A＝72°，请设计三种不同的分法，将菱形ABCD分割成四个三角形，使得每个三角形都是等腰三角形．（画图工具不限，要求画出分割线段；标出能够说明分法所得三角形内角的度数，没有标出能够说明分法所得三角形内角度数不给分；不要求写出画法，不要求证明．）
（注：两种分法只要有一条分割线段位置不同，就认为是两种不同的分法）．
2．（重庆市）如图，A、B是两幢地平高度相等、隔岸相望的建筑物，B楼不能到达．由于建筑物密集，在A的周围没有开阔地带，为了测量B的高度只能充分利用A楼的空间，A的各层楼都可到达且能看见B．现仅是的测量工具为皮尺和测量工具为皮尺和测角器（皮尺可用于测量长度，测角器可以测量仰角、俯角或两视线间的夹角）．
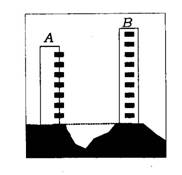
（1）请你设计一个测量B楼高度的方法：要求写出测量步骤和必须测量数据（用字母表示），并画出测量图形；
（2）用你测量的数据（用字母表示），写出计算B楼高度的表达式．
3．（重庆市）实际测试表明1千克重的干衣物，然后用总量为20千克的清水分两次漂洗．假设在洗涤和漂洗的过程中，残留在衣物中的溶液浓度和它所在的溶液中的浓度相等，且每次洗、漂后都需拧干再进入下道操作．问怎样分配这20千克清水的用量，可以使残留在衣物上的洗衣粉溶液浓度最小？残留在衣物上的洗衣粉有多少毫克（保留3个有效数字？）（溶液浓度＝
×100%，1千克106毫克）
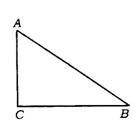
4．（陕西省）如图，△ABC是一块直角三角形余料，∠C＝90°．工人师傅要把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．
（1）试协助工人师傅用尺规画出裁割线（不写作法，保留作图痕迹）
（2）工人师傅测得AC＝80厘米，BC＝120厘米，请帮助工人师傅算出按（1）题所画裁割线加工成的正方形零件的边长．
5．（甘肃省）某公司在甲、乙两座仓库分别有农用车12辆和6辆。现需要调往A县10辆，调往B县8辆，已知从甲仓库调运一辆农用车到A县和B县的运费分别为40元和80元；从乙仓库调运一辆农用车到A县和B县的运费分别为30元和50元．
（1）设从乙仓库调往A县农用车x辆，求总运费y关于x函数关系式；
（2）若要求总运费不超过900元，问共有几种调运方案？
（3）求出总运费最低的调运方案，最低运费是多少元？
6．（山东省）如图（一），是从长为40厘米、宽为30厘米的矩形钢板左上角截取一块长为20厘米、宽为10厘米的矩形后，剩下的一块下脚料。工人师傅要将它作适当的切割，重新拼接后焊成一个面积与原下脚料的面积相等，接缝尽可能短的正方形工件．
（1）请根据上述要求，设计出将这块下脚料适当分割三块或三块以上的两种不同的拼接方案（在图（二）和图（三）中分别画出切割时所沿的虚线，以及拼接后所得到的正方形，保留拼接的痕迹）；
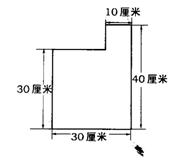
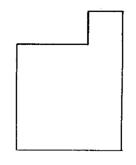
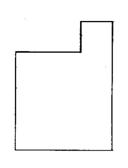
图（一） 图（二） 图（三）
7．（安徽省）某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售量如下：
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
（1）求这15位营销人员该月销售量的平均数、中位数和众数；
（2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由．
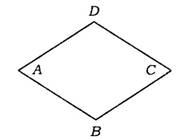
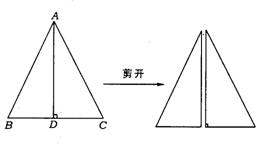
8．（新疆乌鲁木齐）如图，已知在△ABC中，AB＝AC，AD⊥BC于D，且AD＝BC＝4．若将此三角形沿AD剪开成为两个三角形，在平面上把这两个三角形拼成一个四边形，你能拼出所有的不同形状的四边形吗？画出所拼四边形的示意图（标出图中的直角），并分别写出所拼四边形的对角线的长（不要求写计算过程，只须写出结果）．
9．（镇江市）某企业有员工300人，生产A种产品，平均每人每年可创造利润m万元（m为大于零的常数）．为减员增效，决定从中调配x人去生产新开发的B种产品．根据评估，调配后，继续生产A种产品的员工平均每人每年创造的利润可增加20％，生产B种产品的员工平均每人每年可创造利润1.54m万元．
（1）调配后，企业生产A种产品的年利润为_________万元，企业生产B种产品的年利润为________万元（用含x和m的代数式表示）．若设调配后企业全年总利润为，y万元，则y关于x的函数解析式为__________．
（2）若要求调配后，企业生产A种产品的年利润不小于调配前企业年利润的
，生产B种产品的年利润大于调配前企业年利润的一半，应有哪几种调配方案？请设计出来并指出其中哪种方案全年总利润最大（必要时，运算过程可保留3个有效数字）．
（3）企业决定将“（2）”中的年最大总利润（设m＝2）继续投资开发新产品．现有6种产品可供选择（不得重复投资同一种产品），各产品所需资金及所获利润如下表：
如果你是企业决策者，为使此项投资所获年利润不少于145万元，你可以投资开发哪些产品？请写出两种投资方案．
10．（昆明市）某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元；设矩形一边长为x米，面积为S平方米．
（1）求出S与x之间的函数关系式，并确定自变量x的取值范围；
（2）请你设计一个方案，使获得的设计费最多，并求出这个费用；
（3）为使广告牌美观、大方，要求做成黄金矩形，请你按要求设计，并计算出可获得的设计费是多少（精确到元）．
[参考资料：①当矩形的长是宽与（长＋宽）的比例中项时，这样的矩形叫做黄金矩形．②
＝2．236]．
11．（山西省）如图，有一破残的轮片，现要制作一个与原轮片同样大小的圆形零件，请你根据所学的有关知识，设计两种方案，确定这个圆形零件的半径．
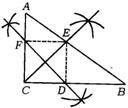
12．（江西省）如图，AB＝AE，∠ABC＝∠AED，BC＝ED，点F是CD的中点．
（1）求证：AF⊥CD；
（2）在你连接BE后，还能得出什么新的结论？请写出三个（不要求证明）
参考答案
1．解：参考画法如下图所示
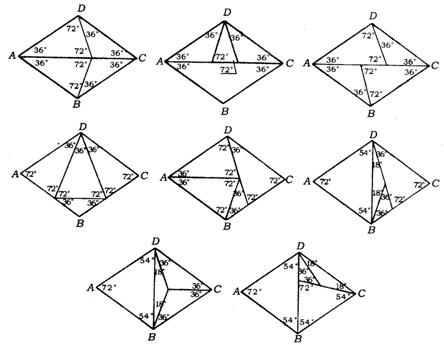
2．解：（１）设AC表示A楼，BD表示B楼．
测量步骤为：如图，①用测角器在A楼的顶端A点测量到B楼底端的俯角α；
②用测角器在点A测量到B楼楼顶的仰角β；
③皮尺从A楼顶放下，测量点A到地面的高为a；
（２）如图，在RtΔACD中，CD＝a×tan∠DAC＝a·cotα，
在RtΔAEB中，BE＝AE·tanβ，
∵AE＝CD，∴ BE＝a·cotα·tanβ，
∴ 楼高BD＝BE＋ED＝BE＋AC＝ a·cotα·tanβ＋a＝a（1＋ cotα·tanβ）
3．设第一次用水x千克，则第二次用水为（20－x）千克．
由题设，衣物拧干后，所带溶液质量与衣物质量相等．
当用洗衣粉洗涤0.5千克干衣拧干后，衣物所带浓度为１％的溶液共处0.5千克，
那么，第一次用x千克水漂洗后的浓度为：
，
第二次加入（20－x）千克水漂洗后的浓度为：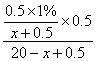
．
化简，得＝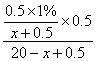
＝
．
显然，当x＝10时分母的取值最大，其分数值最小．
故，用水的方法是每次使用10千克可使残留在衣物上的溶液浓度最小．
第二次漂洗拧干后，残留在衣物上的溶液为0.5千克，其浓度为
．
故，残留的洗衣粉质量为：
千克＝
毫克≈11.3毫克．
答：每次漂洗用水10千克可以使残留在衣物上的溶液浓度最小，残留的洗衣粉有11.3毫克．
4．（１）如图所示，线段DE、EF即为裁剪线．
（２）解：设这个正方形零件的边长为x厘米，
∵ DE//AC，
∴ 
＝
. ∴ 
＝
.
解得x＝48（厘米）．
答：这个正方形零件的边长为48厘米．
5．解：（１）y＝30x＋50（6－x）＋80（8－6＋x）＋40（12－2－x）
＝30x＋300－50x＋160＋80x＋400－40x
＝20x＋860．
（２）20x＋860≤900，x≤2．
∵ 0≤x≤6，
∴ 0≤x≤2．
因为x为非负整数，所以x的取值为0，1，2．
因此，共有三种调运方案．
（３）∵y＝20x＋860，且x的取值为0，1，2．
由一次函数的性质得x＝０时，y的值最小，y
＝860（元）．
此时的调运方案是：乙仓库的6辆全部运往B县，10辆运往A县，最低运费为860元．
6．解：∵ 拼接后正方形的边长为
厘米，它恰是以30厘米和10厘米为两直角边的直角三角形的斜边的长，为此可考虑设法在原钢板上构造两直角边长分别为30厘米、10厘米的直角三角形．
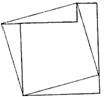
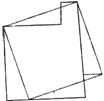
图（一） 图（二） 图（三）
（1）图（一）～图（三）是将钢板分别切割成三块、四块和五块后的几种不同的设计方案．
（2）图（一）和图（二）的方案好些．
∵ 图（一）的接缝长为：30＋30＋10＝70（厘米），
图（二）的接缝长为：20＋10×
＋30＋10＋10×
＝70（厘米），
图（三）的接缝长为：30＋30＋10×＋10×＋10＝80（厘米）．
7．解：（１）平均数为：
＝320(件)；
中位数为：210（件）．
众数为：210（件）．
（２）不合理．因为15人中有13人的销售额达不到320件，（320虽是所给一组数据的平均数，它却不能反映营销人员的一般水平．）销售额定为210件合适一些，因为既是中位数，又是众数，是大部分人能达到的定额．
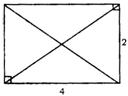
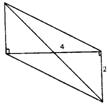
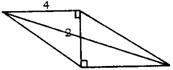
8．经过适当拼合可以组成以下四种不同形状的四边形
①矩形：此时两条对角线的长相等，均为2；
②平行四边形：此时两条对角线的长分别为4和4
；
③平行四边形：此时两条对角线的长分别为2和2
；
④四边形：此时两条对角线的长分别为2和
．
图① 图②
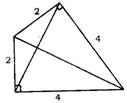
图③ 图④
9．（1）（300－x）（1＋20%）m，1.54mx，
y＝（300－x）（1＋20%）m＋1.54mx．
（2）由题意，得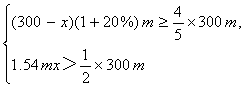
解得97
＜x≤100，
写“97.5＜x≤100”，或“97.４＜x≤100”均视为正确．
∵ x为整数，
∴ x只能取98，99，100．
故共有三种调配方案：
①202人继续生产A种产品，调98人生产B种产品；
②201人继续生产A种产品，调99人生产B种产品；
③200人继续生产A种产品，调100人生产B种产品．
又y＝（300－x）（1＋20%）m＋1.54mx＝0.34mx＋360m，
由于0.34m＞0，函数y随x的增大而增大，故当x＝100．
即按第三种方案安排生产时，获总利润最大．
（3）当m＝2时，最大总利润为788万元．
根据题意，可投资开发产品F、H或C、D、E，或C、D、G或C、F、G．
10．解：（1）S与x之间的函数关系式为S＝x（6－x）＝－x2＋6x，其中0＜x＜6．
（2）S＝－x2＋6x＝－（x－3）2＋9
即：矩形广告牌设计为边长为3米的正方形时，矩形的面积最大，为9平方米；
此时可获得最多设计费，为9×1000＝9000（元）
（3）设此黄金矩形的长为x米，宽为y米，
则由题意可知：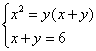
解得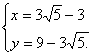
（x＝－3－3不合题意，舍去）
即：当把矩形的长设计为3－3米时，
此矩形将成为黄金矩形．
此时S＝xy（3－3）（9－3）＝36（－2）．
可获得的设计费为：36（－2）×100≈8496（元）
11．解：
方案1：作图法
在残片弧上任取三点A、B、C，连结AC、CB，分别作AC、BC的中垂线交于点O．则OA的长即为所求半径．
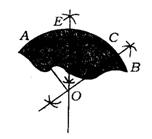
方案2：在上图中，测出弦AC、弓形高DE的长．
设半径为r，由相交弦定理，得（
AC）2＝DE·（2r－DE），
或由勾股定理r2＝（AC）2＋（r－DE）2，解方程求出r即可．
11．（1）证明：连结AC、AD，∵ AB＝AE，∠ABC＝∠AED，BC＝ED，
∴ △ABC≌△AED． ∴AC＝AD．又∵ F为CD中点，∴ AF⊥CD．
（2）①BE∥CD ②AF⊥BE ③△ACF≌△ADF． ④∠BCF＝∠EDF ⑤五边形ABCDE是以直线AF为对称轴的轴对称图形．
