中等学校招生统一考试数学试题
一、选择题(下列各题给出的四个选项中,只有一个是正确的.每小题3分)
1.![]() 的倒数为
的倒数为
(A)2 (B)![]() (C)
(C)![]() (D)
(D)![]()
2.计算![]() 的结果是
的结果是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.近年来,我市旅游产业迅速发展.据统计,2003年全市实现旅游收入41亿元,则此收入值(单位:元)用科学记数法可表示为
(A) ![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D) ![]()
4.关于函数![]() ,下列结论正确的是
,下列结论正确的是
(A)函数图象必经过点(1,2) (B)函数图象经过第二、四象限
(C)y随x 的增大而增大
(D)不论x 取何值,总有![]()
5.下列图案中,既是中心对称又是轴对称的图案是



(A) (B) (C) (D)
6.某种商品进价为a元/件,在销售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为
(A) a元 (B)0.7 a元 (C)1.03 a元 (D)0.91a元
7.关于x的一元二次方程![]() 有实数根,则k的取值范围是
有实数根,则k的取值范围是
(A)![]() (B)
(B)![]() ≤
≤![]() (C)
(C)![]() (D)
(D)![]() ≥
≥![]()
8.若⊙![]() 的圆心坐标为
的圆心坐标为![]() ,半径为1;⊙
,半径为1;⊙![]() 的圆心坐标为
的圆心坐标为![]() ,半径为3,则这两圆的位置关系是
,半径为3,则这两圆的位置关系是
(A) 相交 (B) 相切 (C) 相离 (D) 内含
10.在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 11.如图,已知⊙
11.如图,已知⊙![]() 的半径为5,点A到圆心O的距离
的半径为5,点A到圆心O的距离
为3,则过点A的所有弦中,最短弦的长为
(A)4 (B)6
(C)8 (D)10
12.甲、乙两辆摩托车分别从![]() 、
、![]() 两地出发相向而
两地出发相向而
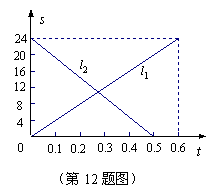 行,图中
行,图中![]() 、
、![]() 分别表示两辆摩托车与
分别表示两辆摩托车与![]() 地的距
地的距
离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关
(小时)之间的函数关
系,则下列说法:①![]() 、
、![]() 两地相距24千米;
两地相距24千米;
②甲车比乙车行完全程多用了0.1小时;③甲车
的速度比乙车慢8千米/小时;④两车出发后,
经过![]() 小时,两车相遇.其中正确的有
小时,两车相遇.其中正确的有
(A)1个 (B)2个
(C)3个 (D)4个
二、填空题(每小题3分,共18分.请将答案直接填在题中横线上)
13.将![]() 因式分解,其结果是
.
因式分解,其结果是
.
14.函数![]() 中自变量
中自变量![]() 的取值范围是
.
的取值范围是
.
 15.如果四边形
15.如果四边形![]() 满足条件:
,那么这个四边形的对角线
满足条件:
,那么这个四边形的对角线![]() 和
和![]() 相等.(只需填写一个你认为适当的条件即可)
相等.(只需填写一个你认为适当的条件即可)
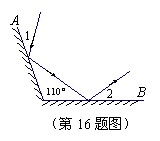
16.如图,平面镜A与B之间夹角为110°,光
线经平面镜A反射到平面镜B上,再反射出
去,若![]() ,则
,则![]() 的度数为 .
的度数为 .
17.如果圆锥的底面半径是4,母线的长是16,
那么这个圆锥侧面展开图的扇形的圆心角的
度数是 .
18.某科技小组制作了一个机器人,它能根据指令要求进行行走和旋转.某一指令规定:机器人先向正前方行走1米,然后左转![]() .若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了 米.
.若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了 米.
三、解答题 (共76分)
| 得分 | 评卷人 | 复评人 |
19.(每小题满分6分,共12分)
(1)计算![]() ·
·![]() ;
;
(2)解方程![]() .
.
| 得分 | 评卷人 | 复评人 |
20.(本小题满分6分)
 已知:如图,
已知:如图,![]() 、
、![]() 、
、![]() 、
、![]() 四点在一直线上,
四点在一直线上,![]() ,
,![]() ∥
∥![]() ,且
,且![]() .
.
求证:(1)![]() ≌
≌![]() ;
;
(2)![]() .
.
| 得分 | 评卷人 | 复评人 |
21.(本小题满分6分)
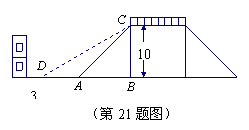 下图是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为
下图是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为![]() .为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为
.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为![]() ,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?(参考数据:
,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732 )
≈1.732 )
| 得分 | 评卷人 | 复评人 |
22.(本小题满分6分)
某小区响应市政府号召,开展节约用水活动,效果显著.为了解某居民小区节约用水情况,随机对该小区居民户家庭用水情况作抽样调查,3月份较2月份的节水情况如表所示(在每组的取值范围中,含最低值,不含最高值):
| 节水量(吨) | 0.2~0.6 | 0.6~1.0 | 1.0~1.4 | 1.4~1.8 | 1.8~2.2 |
| 户数 | 5 | 20 | 35 | 30 | 10 |
(1)试估计该小区3月份较2月份节水量不低于1吨的户数占小区总户数的百分比;
(2)已知该小区共有居民5000户,若把每组中各个节水量值用该组的中间值(如0.2~0.6的中间值为0.4)来代替,请你估计该小区3月份较2月份共节水多少吨?
| 得分 | 评卷人 | 复评人 |
23. (本小题满分8分)
有一个运算装置,当输入值为x时,其输出值为![]() ,且
,且![]() 是x的二次函数,已知输入值为
是x的二次函数,已知输入值为![]() ,0,
,0,![]() 时, 相应的输出值分别为5,
时, 相应的输出值分别为5,![]() ,
,![]() .
.
(1)求此二次函数的解析式;
(2)在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值![]() 为正数时输入值
为正数时输入值![]() 的取值范围.
的取值范围.
 |
| 得分 | 评卷人 | 复评人 |
24.(本小题满分8分)
据统计,连云港港口2002年、2003年的内外贸吞吐总量分别为3300万吨和3760万吨,其中2003年外贸和内贸吞吐量分别较2002年增长10%和20%.
(1)试确定2002年的外贸和内贸吞吐量;
(2)2004年港口内外贸吞吐量的目标是:总量不低于4200万吨,其中外贸吞吐量所占比重不低于60%.预计2004年的内贸吞吐量较2003年增长10%,则为完成上述目标,2004年的外贸吞吐量较2003年至少应增加多少万吨?
| 得分 | 评卷人 | 复评人 |
25.(本小题满分10分)
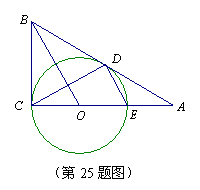 已知:如图,Rt
已知:如图,Rt![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为圆心、OC为半径的圆与AB相切于点
为圆心、OC为半径的圆与AB相切于点![]() ,交AC于点E.
,交AC于点E.
(1)求证:DE∥OB;
(2)若⊙O的半径为2,![]() ,求AD的长.
,求AD的长.
| 得分 | 评卷人 | 复评人 |
26、(本小题满分10分)
 (1)如图,在梯形ABCD中,AB∥CD,
(1)如图,在梯形ABCD中,AB∥CD,![]() ,
,![]() ,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
①当![]() 时,有
时,有![]() ;
;
②当![]() 时,有
时,有![]() ;
;
③当![]() 时,有
时,有![]() .
.
当![]() 时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;
时,参照上述研究结论,请你猜想用k表示DE的一般结论,并给出证明;
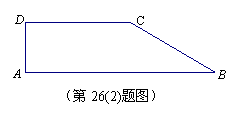 (2)现有一块直角梯形田地
(2)现有一块直角梯形田地![]() (如图所示),其中AB∥CD,
(如图所示),其中AB∥CD,![]() ,
,![]() 310米,
310米,![]() 170米,
170米,![]() 70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
| 得分 | 评卷人 | 复评人 |
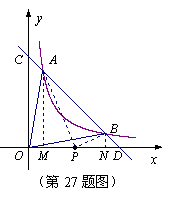
27.(本小题满分10分)
对于函数![]() ,解答下述问题:
,解答下述问题:
(1)若函数在![]() 内有意义,求实数a的取值范围;
内有意义,求实数a的取值范围;
(2)若函数的定义域为![]() ,求实数a的值;
,求实数a的值;
(3)若函数的值域为![]() ,求实数a的值;
,求实数a的值;
数学试题参考答案及评分标准
一、选择题:BAACBD BADBCD
二、填空题:13.![]() ; 14.
; 14.![]() ; 15.四边形
; 15.四边形![]() 为矩形(本题答案不唯一,其它答案如四边形
为矩形(本题答案不唯一,其它答案如四边形![]() 为正方形(或等腰梯形)
为正方形(或等腰梯形)![]() ≌
≌![]() 等); 16.
等); 16.![]() ; 17.90; 18. 8.
; 17.90; 18. 8.
三、解答题:
19.(1)解:原式= (![]() )
)![]() +(2 +
+(2 +![]() ) …………………………(5分)
) …………………………(5分)
= 1. …………………………(6分)
(2)解:方程两边同乘以![]() ,得
,得
![]() , …………………………(2分)
, …………………………(2分)
即![]() , …………………………(3分)
, …………………………(3分)
解之得![]() ,
,![]() , …………………………(4分)
, …………………………(4分)
经检验![]() 是原方程的增根,
是原方程的增根,
所以原方程的根为![]() . …………………………(6分)
. …………………………(6分)
20.证:(1)![]() A、F、C、D四点共线且AF =
CD,
A、F、C、D四点共线且AF =
CD,
∴![]() ,即AC = DF. …………………………(1分)
,即AC = DF. …………………………(1分)
![]() AB∥DE, ∴
AB∥DE, ∴![]() ,
…………………………(2分)
,
…………………………(2分)
又![]() AB=DE,∴
AB=DE,∴![]() ≌
≌![]() .
…………………………(3分)
.
…………………………(3分)
(2)由![]() ≌
≌![]() 得
得![]() ,EF=BC,
,EF=BC,
又CF为公共边,∴![]() ≌
≌![]() . …………………………(5分)
. …………………………(5分)
∴![]() . …………………………(6分)
. …………………………(6分)
21.解:在Rt![]() 中,∵
中,∵![]() ,
,![]() ,∴ AB=
,∴ AB=![]() =10(米)
=10(米)
在Rt![]() 中,∵
中,∵![]() ∴
∴![]() =
=![]() 米 …………(4分)
米 …………(4分)
则DA =![]() =
= ![]() ≈10×1.732
≈10×1.732![]() = 7.32米. …………(5分)
= 7.32米. …………(5分)
∵3 + DA![]() ,所以离原坡角10米的建筑物应拆除.
,所以离原坡角10米的建筑物应拆除.
答:离原坡角10米的建筑物应拆除. …………………………(6分)
22.解:(1)3月份较2月份节水量不低于1吨的用户数为35 + 30 + 10 = 75,
又样本总量为5 + 20 + 75 = 100(户),故所求的百分比为![]() = 75%.
= 75%.
答:3月份较2月份节水量不低于1吨的户数占小区总户数的百分比为75%.(3分)
(2)节水量各组的中间值依次为0.4,0.8,1.2,1.6,2.0.故抽样的100户总节水量约为0.4×5 + 0.8×20 +1.2×35 +1.6×30 +2.0×10 =128(吨). …………(5分)
所以全小区居民户的总节水量约为![]() = 6400(吨).
= 6400(吨).
答: 该小区居民户3月份较2月份共节水约6400吨. ………………………(6分)
23.解:(1)设所求二次函数的解析式为![]() ,
,
 则
则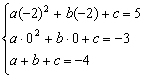 ,即
,即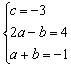 ,解得
,解得![]()
故所求的解析式为:![]() . ……………(4分)
. ……………(4分)
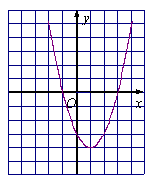
2)函数图象如图所示. …………………………(7分)
由图象可得,当输出值![]() 为正数时,
为正数时,
输入值![]() 的取值范围是
的取值范围是![]() 或
或![]() . ………(8分)
. ………(8分)
24.解:(1)设2002年内贸、外贸吞吐量分别为x和y万吨,
则![]() ……………………(2分)
……………………(2分)
解得![]() ,
,
答:2002年内贸、外贸吞吐量分别为1300万吨和2000万吨.……………………(4分)
(2)设2004年较2003年外贸吞吐量增加z万吨.
又2003年内贸吞吐量为1300×(1+20%) =1560(万吨),
2003年外贸吞吐量为3760![]() (万吨).
(万吨).
则![]() ……………………(6分)
……………………(6分)
解得![]() .
.
答:2004外贸吞吐量较2003年至少应增加374万吨. ……………………(8分)
25.证:(1)∵![]() ,
,![]() 是⊙O的半径,
是⊙O的半径,
∴BC是⊙O的切线,又∵AB与⊙O相切,
∴OC = OD,且BO为![]() 的角平分线,∴BO
的角平分线,∴BO![]() CD, ……………………(3分)
CD, ……………………(3分)
又∵![]() 是⊙O 的直径,且
是⊙O 的直径,且![]() 是⊙O 上一点,
是⊙O 上一点,
∴DE![]() CD,∴
CD,∴![]() ∥OB.
……………………(5分)
∥OB.
……………………(5分)
(2) ∵![]() ∥OB ,∴
∥OB ,∴![]() ,
,
又![]() ,
,![]() ,∴
,∴![]() ,即
,即![]() . ………………(7分)
. ………………(7分)
又![]() 、
、![]() 分别是⊙O的切线和割线,
分别是⊙O的切线和割线,
∴![]() ·
·![]() ,即
,即![]() ·
·![]() ,
……………………(9分)
,
……………………(9分)
∴![]() ·
·![]() ,可得
,可得![]() . ……………………(10分)
. ……………………(10分)
26.(1)解:猜想得:EF =![]() .
……………………………(2分)
.
……………………………(2分)
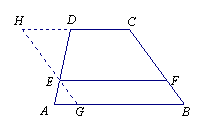 证明:过点E作BC的平行线交AB于G,交CD的延长线于H.
证明:过点E作BC的平行线交AB于G,交CD的延长线于H.
∵AB∥CD,∴![]() ∽
∽![]() ,∴
,∴![]() ,
,
又![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,可得
,可得![]() .…………………(5分)
.…………………(5分)
(2)在![]() 上取一点E,作EF∥AB交BC于点F,设
上取一点E,作EF∥AB交BC于点F,设![]() ,
,
则EF=![]() ,
,![]() ,
…………(7分)
,
…………(7分)
若![]() ,则
,则![]() ,
,
∵梯形ABCD、DCFE为直角梯形,
∴![]()
![]() ,
,
化简得![]() 解得:
解得:![]() ,
,![]() (舍去),
…………(9分)
(舍去),
…………(9分)
∴![]() ,
,
所以只需在AD上取点E,使![]() 米,作EF∥AB(或
米,作EF∥AB(或![]() ),
),
即可将梯形分成两个直角梯形,且它们的面积相等. …………(10分)
27.解:设![]() ,
,![]() (其中
(其中![]() ),
),
由![]() ,得
,得![]()
∴![]() ·
·![]() ·
·![]() (
(![]() ·
·![]() ·
·![]()
![]() ·
·![]() ·
·![]() ),
),![]() ,…………(2分)
,…………(2分)
又![]() ,∴
,∴![]() ,即
,即![]() ,……………………(3分)
,……………………(3分)
 由
由![]() 可得
可得![]() ,代入
,代入![]() 可得
可得![]() ①
①
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
又方程①的判别式![]() ,
,
∴所求的函数关系式为![]()
![]() .………………(5分)
.………………(5分)
(2)假设存在![]() ,
,![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
则![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() .
.
∵![]() 与
与![]() 都与
都与![]() 互余,∴
互余,∴![]()
![]() .……………………(6分)
.……………………(6分)
∴Rt![]() ∽Rt
∽Rt![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() , ∴
, ∴![]() ,
,
即![]() ② …………………………(8分)
② …………………………(8分)
由(1)知![]() ,
,![]() ,代入②得
,代入②得![]() ,
,
∴![]() 或
或![]() ,又
,又![]() ,∴
,∴![]() 或
或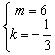 ,
,
∴存在![]() ,
,![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ,且
,且![]() 或
或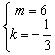 .…(10分)
.…(10分)