中考数学试题及参考答案
一、选择题（本题有12小题,每小题4分，共48分）下列各题所附的四个选项中，有且只有一个是正确的,请把正确选项前面的字母填在题后的括号内
1．比－1小1的数是（ ）
A．－1 B．0 C． 1 D．－2
2．下列运算正确的是（ ）
A．a3－a2=a B．a3·a2=a5 C．a3+a=a4 D． （a2）3=a5
3．函数
的自变量x取值范围是（ ）
A．x≥2 B．x＞2 C．x≠2 D．x＜2
4．已知正比例函数y=kx的图象经过点（1，2），则k的值为（ ）
A．
B．1
C．2 D．4
5．设有12只型号相同的杯子，其中一等品7只，二等品3只，三等品2只，则从中任取1只，是二等品的概率等于（ ）
A．
B．
C．
D．
6．在平面直角坐标系中，两圆的圆心坐标分别为（0，1）和（1，0），半径都是1，那么这两圆的位置关系是（ ）
A．外离 B．相切 C．相交 D．内含
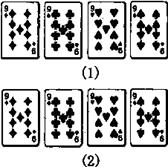
7．4张扑克牌如图（1）所示放在桌面上，小敏把其中一张旋转180°后得到如图（2）所示，那么她所旋转的牌从左数起是（ ）
A．第一张 B．第二张
C．第三张 D．第四张
8．一个圆锥的底面半径为
，母线长为6，则此圆锥侧面展开图的圆心角是（ ）
A．180° B．150°
C．120° D．90°
9．如图，在
ABCD中，E为DC边的中点，AE交BD于点O.若S△DOE=9，则S△AOB等于（ ）
A．18 B．27 C．36 D．45
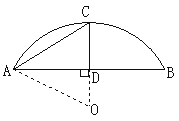
10．圆弧形蔬菜大棚的剖面如图所示，AB=8m，∠CAD=30°，则大棚高度CD约为（ ）
A．2.0 m B．2.3 m C．4.6 m D．6.9 m
11．已知∠AOB=30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1，O，P2三点所构成的三角形是（ ）
A．直角三角形 B．钝角三角形 C．等腰三角形 D．等边三角形
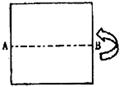
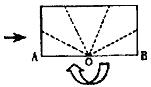
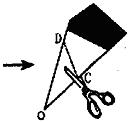
12．如图，一张长方形纸沿AB对折，以AB中点O为顶点将平角五等分，并沿五等分的折线折叠，再沿CD剪开，使展开后为正五角星（正五边形对角线所构成的图形）.则∠OCD等于（ ）
A．108° B．144° C．126° D．129°
二、填空题（本题有6小题，每小题5分，共30分）
13.鲁迅先生十分重视精神文化方面的消费，据史料记载，在他晚年用于购书的费用约占收入的15.6%，则近似数15.6%有 有效数字.
14.在△ABC中，CD⊥AB，请你添加一个条件，写出一个正确结论（不在图中添加辅助线）.
条件： ，
结论： .
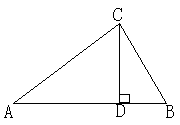
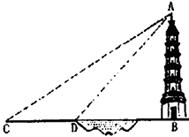
15如图，河对岸有古塔AB.小敏在C处测得塔顶A的仰角为α，向塔前进s米到达D，在D处测得A的仰角为β则塔高是 米.
16.某城市自来水收费实行阶梯水价，收费标准如下表所示，用户5月份交水费45元，则所用水为 度.
| 月用水量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准（元/度） | 2.00 | 2.50 | 3.00 |
17.如图，已知AD=30，点B，C是AD上的三等分点，分别以AB，BC，CD为直径作圆，圆心分别为E，F，G，AP切⊙G于点P，交⊙F于M，N，则弦MN的长是 .
18.用计数器探索：按一定规律排列的一组数：
，
，，…，
，
，如果从中选出若干个数，使它们的和大于0.5，那么至少要选
个数.
三、解答题（本题有7小题，共72分）以下各小题都必须写出解答过程
19.（本题8分）
已知a，b是互为相反数，c，d是互为倒数，e是非零实数.求
的值.
20. （本题8分）
（1） 化简：
；
（2） 若m，n是方程x2－3x+2=0的两个实根，求第（1）小题中代数式的值.
21. （本题10分）
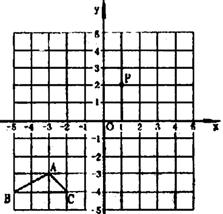
如图，在平面直角坐标系中，已知△ABC，点P（1，2）.
（1）作△PQR，使△PQR与△ABC相似（不要求写出作法）；
（2）在第（1）小题所作的图形中，求△PQR与△ABC的周长比.
22. （本题10分）
初三（2）班的一个综合实践活动小组去A，B两个超市调查去年和今年“五一节”期间的销售情况，下图是调查后小敏与其他两位同学交流的情况.根据他们的对话，请你分别求出A，B两个超市今年“五一节” 期间的销售额.
23. （本题10分）
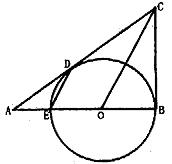
如图，CB，CD是⊙O的切线，切点分别为B，D.CD的延长线与⊙O直径BE的延长线交于A点，连OC，ED.
（1） 探索OC与ED的位置关系，并加以证明；
（2） 若AD=4，CD=6，求tan∠ADE的值.
24. （本题12分）
课本第五册第65页有一题：
已知一元二次方程
的两个根满足
，且a，b，c分别是△ABC的∠A，∠B，∠C的对边.若a=c，求∠B的度数.
小敏解得此题的正确答案“∠B=120°”后，思考以下问题，请你帮助解答.
（1）
若在原题中，将方程改为
，要得到∠B=120°，而条件“a=c”不变，那么应对条件中的
的值作怎样的改变？并说明理由.
（2）
若在原题中，将方程改为
（n为正整数，n≥2），要得到∠B=120°，而条件“a=c”不变，那么条件中的的值应改为多少（不必说明理由）？
25. （本题14分）
在平面直角坐标系中，A（－1，0），B（3，0）.
（1） 若抛物线过A，B两点，且与y轴交于点（0，－3），求此抛物线的顶点坐标；
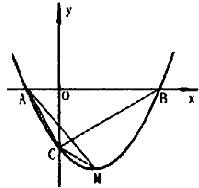
（2） 如图，小敏发现所有过A，B两点的抛物线如果与y轴负半轴交于点C，M为抛物线的顶点，那么△ACM与△ACB的面积比不变，请你求出这个比值；
（3） 若对称轴是AB的中垂线l的抛物线与x轴交于点E，F，与y轴交于点C，过C作CP∥x轴交l于点P，M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形，求次抛物线的解析式.
参考答案
一、选择题（本题有12小题,每小题4分，共48分）
1．D 2．B 3．A 4．C 5．C
6．C 7．A 8．B 9．C 10．B
11．D 12．C
二、填空题（本题有6小题，每小题5分，共30分）
13.3 14.略 15.
16.20
17.8
18.7
三、解答题（本题有7小题，共72分）
19. （本题8分）
=0+－2=
.
20. （本题8分）
（1）=
.
（2）∵ m+n=3，m·n=2， ∴==
.
21. （本题10分）略
22. （本题10分）
设去年A超市销售额为x万元，B 超市销售额为y万元，
由题意得
解得
100（1+15%）=115（万元），50（1+10%）=55（万元）.
答：A，B两个超市今年“五一节” 期间的销售额分别为115万元，55万元.
23. （本题10分）
（1） ED∥OC.
证明（思路）：连OD，BD，证DE⊥BD，CO⊥BD.
（2） ∵ ED∥OC，
∴ ∠ADE=∠ACO.
又∵ CB，CD是⊙O的切线，切点分别为B，D，
∴ ∠BCO=∠ACO，
∴ ∠ADE =∠BCO.
记⊙O的半径为R，
∵ ED∥OC，AD=4，CD=6，
∴ 
， ∴ AE=
.
又∵ AD2=AE·AB，16=·
， ∴ R=3.
即BO=3，而BC=CD=6，
∴ tan∠ADE= tan∠BCO=
.
24. （本题12分）
（1）∵ ∠B=120°，a=c， ∴
b=
a，△=5a2＞0.
又∵ =
=
.
∴ =
.
（2）=
.
25.简解：（1）
，顶点坐标为（1，－4）.
（2）由题意，设y=a（x+1）（x－3），即y=ax2－2ax－3a，
∴ A（－1，0），B（3，0），C（0，－3a），M（1，－4a），
∴
S△ACB=
×4×
=6
，
而a＞0， ∴ S△ACB=6a.
作MD⊥x轴于D，
又S△ACM=S△ACO +SOCMD
－S△AMD=·1·3a+（3a+4a）－·2·4a=a，
∴ S△ACM：S△ACB=1：6.
（3）①当抛物线开口向上时，设y=a（x－1）2+k，即y=ax2－2ax+a+k，
有菱形可知
=
，a+k＞0，k＜0，
∴
k=
，
∴
y=ax2－2ax+
， ∴ 
.
记l与x轴交点为D，
若∠PEM=60°，则∠FEM=30°，MD=DE·tan30°=
，
∴
k=－，a=
，
∴
抛物线的解析式为
.
若∠PEM=120°，则∠FEM=60°，MD=DE·tan60°=
，
∴
k=－，a=
，
∴
抛物线的解析式为
.
②当抛物线开口向下时，同理可得
，
.