各类高中招生考试数学试题
满分120分，考试时间100分钟
一、选择题（本题有15个小题，每小题3分，共45分）下面每小题给出的四个选项中，只有一个是正确的．
1．下列各组数中互为相反数的是（ ）．
（A）
与
（B）
与2 （C）与
（D）与
2．下列各式中计算正确的是（ ）．
（A）
（B）
（C）
（D）
3．用配方法将二次三项式
变形的结果是（
）．
（A）
（B）
（C）
（D）
4．在时刻8∶30，时钟上的时针和分针之间的夹角为（ ）．
（A）85° （B）75° （C）70° （D）60°
5．1米长的标杆直立在水平的地面上，它在阳光下的影长为0.8米；此时，若某电视塔的影长为100米，则此电视塔的高度应是（ ）．
（A）80米 （B）85米 （C）120米 （D）125米
6．已知2是关于x的方程
的一个解，则
的值是（ ）．
（A）3 （B）4 （C）5 （D）6
7．如果直角三角形的三条边为2，4，a，那么a的取值可以有（ ）．
（A）0个 （B）1个 （C）2个 （D）3个
8．不等式组
的解在数轴上可表示为（
）．
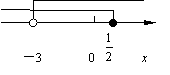
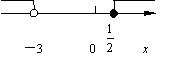
（A） （B）
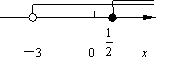
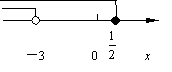
（C） （D）
9．过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm．则OM的长为（ ）．
（A）
cm （B）
cm （C）2cm （D）3cm
10．已知正比例函数
的图象上两点
、
，当
时，有
，那么m的取值范围是（
）．
（A）
（B）
（C）
（D）
11．在△ABC中，∠A、∠B都是锐角，且
，
，则△ABC三个角的大小关系是（
）．
（A）∠C>∠A>∠B （B）∠B>∠C>∠A （C）∠A>∠B>∠C （D）∠C>∠B>∠A
12．用反证法证明：“三角形中必有一个内角不小于60°”，先应当假设这个三角形中（ ）．
（A）有一个内角小于60° （B）每一个内角都小于60°
（C）有一个内角大于60° （D）每一个内角都大于60°
13．下列函数关系中，可以看作二次函数
模型的是（ ）．
（A）在一定的距离内汽车的行驶速度与行驶时间的关系
（B）我国人口年自然增长率为1％，这样我国人口总数随年份的变化关系
（C）竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）
（D）圆的周长与圆的半径之间的关系
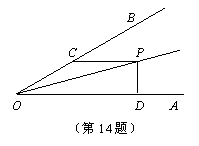
14．如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD等于（ ）．
（A）4 （B）3 （C）2 （D）1
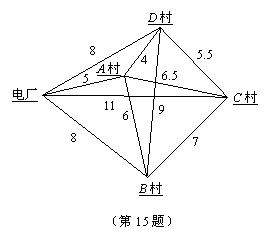
15．为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里），则能把电力输送到这四个村庄的输电线路的最短总长度应该是（ ）．
（A）19.5 （B）20.5 （C）21.5 （D）25.5
二、填空题（本题有5个小题，每小题4分，共20分）
16．
的因式分解的结果是____________________．
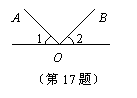17．当图中的∠1和∠2满足________________时，能使OA⊥OB（只需填上一个条件即可）．
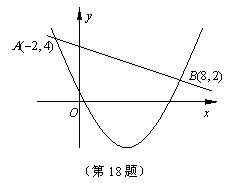18．已知二次函数
与一次函数
的图象相交于点
（如图所示），则能使成立的x的取值范围是____________________．
19．圆锥可以看成是直角三角形以它的一条直角边所在的直线为轴，其余各边旋转一周而成的面所围成的几何体，那么圆台可以看成是___________________________所在的直线为轴，其余各边旋转一周而成的面所围成的几何体；如果将一个半圆以它的直径所在的直线为轴旋转一周，所得的几何体应该是___________．
20．对于反比例函数
与二次函数
，请说出它们的两个相同点①_________________________，②__________________________；再说出它们的两个不同点①_________________________，②__________________________．
三、解答题（本题有6个小题，共55分）．解答应写出文字说明，证明过程或推演步骤．
21．（本小题满分7分）当
时，求代数式
的值．
22．（本小题满分8分）如图，小王在陆地上从A地经B地到达C地总行程是14千米，这里的∠ABC为直角，且∠BAC的正切值为0.75．那么小王乘海轮从A地直接到C地的最短距离是多少千米?
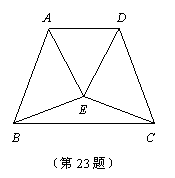
23．（本小题满分8分）已知等腰梯形ABCD，E为梯形内一点，且EA=ED．求证：EB=EC．
24．（本小题满分10分）已知某二次项系数为1的一元二次方程的两个实数根为p、q，且满足关系式
，试求这个一元二次方程．
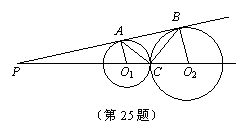
25．（本小题满分10分）如图，⊙O1与⊙O2外切于点C，⊙O1与⊙O2的连心线与外公切线相交于点P，外公切线与两圆的切点分别为A、B，且AC=4，BC=5．
（1）求线段AB的长；（2）证明：
．
26．（本小题满分12分）已知二次函数
．
（1）证明：不论a取何值，抛物线的顶点Q总在x轴的下方；
（2）设抛物线与y轴交于点C，如果过点C且平行于x轴的直线与该抛物线有两个不同的交点，并设另一个交点为点D，问：△QCD能否是等边三角形？若能，请求出相应的二次函数解析式；若不能，请说明理由；
（3）在第（2）题的已知条件下，又设抛物线与x轴的交点之一为点A，则能使△ACD的面积等于
的抛物线有几条？请证明你的结论．