勾股定理
【同步达纲练习】
一、判断(4分×6=24分)
( )1.直角三角形直角边长为6，8，则斜边上的高为2.4.
( )2.直角三角形两边为1，2则另一边为
.
( )3.两直角边的比为1∶的直角三角形三内角比为1∶2∶3.
( )4.等腰直角三角形斜边中线与直角边的比为
∶1.
( )5.面积为12，底边为6的等腰三角形腰长为5.
( )6.高为h的等边三角形面积为
h2.
二、选择(5分×6=30分)
1.周长为24，斜边长为10的直角三角形面积为( )
A.12 B.16 C.20 D.24
2.△ABC中，∠C=90°, ∠A=30°，M为AB中点，MD⊥AB交AC于D.若DM=7，则BC长为( )
A.7
B.14 C.7
D.14
3.直角三角形锐角平分线分对边为15和25两部分，则斜边长为( )
A.50 B.60 C.70 D.80
4.三角形内角比为1∶2∶3，，则三边长度比为( )
A.1∶2∶3 B. 1∶∶2 C.1∶∶ D.1∶∶3
5.直角三角形斜边上的高分斜边为1∶2两部分，则三条高的比为( )
A.1∶∶2
B.∶∶
C.1∶∶ D.∶∶2
6.顶角为150°的等腰三角形，腰上的高与腰的比为( )
A.1∶2
B.1∶
C.∶2
D.1∶3
三、填空(5分×6=30分)
1.已知线段a,求作线段
a时，可分别以2a和 为直角边作直角三角形，斜边即为所求.
2.等腰直角三角形直角边长为1，则斜边长为 .
3.等边三角形边长为2，则面积为 .
4.CD为Rt△ABC斜边上的高，AB=13，AC=12，则CD= .
5.周长为30，面积也为30的直角三角形斜边中线长为 .
6.两直角边之和为14，斜边长为12的直角三角形斜边上的高是 .
四、解答题(8分×2=16分)
1.计算:Rt△ABC中，∠C=Rt∠,CD⊥AB于D，M为AB中点，MD=CD，求∠B.
2.△ABC中，D为BC上一点，且AB=AD，求证AC2-AB2=BC·DC.
【素质优化训练】
1.若a,b,c,为Rt△ABC三边的长，c为斜边长，斜边上的高为h.求证c+h＞a+b.
2.△ABC中，AB=18，BC=17，AC=18，P为形内一点，PD⊥BC于D.PE⊥AC于E.PF⊥AB于F，且BD+CE+AE=27，求BD+BF的值.
【生活实际运用】
(如图3.16-8)某校A与直线公路距离为3000米，又与该公路上某车站D的距离为5000米，现要在公路边建一个小商店C，使之与学校A及车站D的距离相等，那么，该店与车站D的距离是多少米？
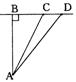
图3.16-8
【知识探究学习】
利用勾股定理求线段长：若求直角三角形的边长，可由勾股定理列出含待求线段的等式即含待求线段的方程，设法解这个方程.
参考答案
【同步达纲练习】
一、× × √ × √ ×
二、D C A B B A
三、1.3a 2. 3. 4.
5.
6.
四、1.∵CD⊥AB CD=MD ∴∠CMB=45° 又CM=MB ∴∠B=67.5°
2.作AE⊥BD于E，∵AB=AD ∴ED=EB.
∴AC2-AB2=(EC2+AE2)-(EB2+AE2)=(EC+EB)(EC-ED)=BC·DC
【素质优化训练】
1.∵a2+b2=c2 ab=ch
∴(a+b)2=a2+b2+2ab=c2+2ch＜(c+h)2
∴c+h＞a+b.
2.设BD=x CE=y AF=z,PD=a PE=b PF=c 则CD=17-x AE=18-y BF=19-z
∴x2+a2=(19-z)2+c2① y2+b2=(17-x)2+a2② z2+c2=(18-y)2+b2③ ①+②+③整理得：
17x+18y+19z=18×27+1
又x+y+z=27 ∴18x+18y+18z=18×27 ∴z-x=1.BD+BF=x+19-z=19-(z-x)=19-1=18.
【生活实际运用】
3125米