普通高中招生统一考试数学试卷9
(本卷共四大题,满分150分,考试时间:120分钟)
一、选择题:(本大题12个小题,每小题4分,共48分)
1、下列各组数中,互为相反数的是( )
A、2与![]() B、
B、![]() 与1 C、-1与
与1 C、-1与![]() D、2与∣-2∣
D、2与∣-2∣
2、下列一元二次方程中,没有实数根的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
 3、如图,⊙O中弦AB、CD相交于点F,AB=10,AF=2。若CF∶DF=1∶4,则CF的长等于( )
3、如图,⊙O中弦AB、CD相交于点F,AB=10,AF=2。若CF∶DF=1∶4,则CF的长等于( )
A、![]() B、2
B、2
C、3
D、2![]()
4、三峡大坝从6月1日开始下闸蓄水,如果平均每天流入库区的水量为![]() 立方米,平均每天流出的水量控制为
立方米,平均每天流出的水量控制为![]() 立方米。当蓄水位低于135米时,
立方米。当蓄水位低于135米时,![]() <
<![]() ;当蓄水位达到135米时,
;当蓄水位达到135米时,![]() =
=![]() ;设库区的蓄水量
;设库区的蓄水量![]() (立方米)是时间
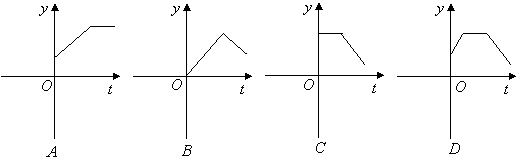
(立方米)是时间![]() (天)的函数,那么这个函数的大致图象是( )
(天)的函数,那么这个函数的大致图象是( )
5、随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费标准按原标准每分钟降低了![]() 元后,再次下调了25%,现在的收费标准是每分钟
元后,再次下调了25%,现在的收费标准是每分钟![]() 元,由原收费标准每分钟为( )
元,由原收费标准每分钟为( )
A、![]() 元 B、
元 B、![]() 元 C、
元 C、![]() 元 D、
元 D、![]() 元
元
6、如下图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )
A、![]() B、7
C、
B、7
C、![]() D、
D、![]()
7、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … |
|
|
|
|
| … |
那么,当输入数据是8时,输出的数据是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()



8、已知:如图,梯形ABCD中,AD∥BC,∠B=450,∠C=1200,AB=8,则CD的长为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、某班学生在颁奖大会上得知该班获得奖励的情况如下表:
|
人数 级别 | 三好学生 | 优秀学生干部 | 优秀团员 |
| 市级 | 3 | 2 | 3 |
| 校级 | 18 | 6 | 12 |
已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A、3项 B、4项 C、5项 D、6项
10、如图:△ABP与△CDP是两个全等的等边三角形,且PA⊥PD。有下列四个命题:①∠PBC=150;②AD∥BC;③直线PC与AB垂直;④四边形ABCD是轴对称图形。其中正确结论的个数为( )
A、1 B、2 C、3 D、4
 11、如图:在等腰直角三角形ABC中,∠C=900,AC=6,D是AC上一点,若tan
∠DBA=
11、如图:在等腰直角三角形ABC中,∠C=900,AC=6,D是AC上一点,若tan
∠DBA=![]() ,则AD的长为( )
,则AD的长为( )
A、![]() B、2
B、2
C、1
D、2![]()
12、在平行四边形ABCD中,AB=6,AD=8,∠B是锐角,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处。如果AE过BC的中点,则平行四边形ABCD的面积等于( )
A、48 B、![]() C、
C、![]() D、
D、![]()
二、填空题:(本大题8个小题,每小题4分,共32分)
13、分解因式:![]() =
。
=
。
14、计算:![]() =
。
=
。
15、如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=460,∠DCF=320,则∠A的度数是 。

16、已知![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个实数根,且
的两个实数根,且![]() +
+![]() =
=![]() ,则
,则![]() =
。
=
。
17、已知关于![]() 的不等式组
的不等式组![]() 无解,则
无解,则![]() 的取值范围是 。
的取值范围是 。
18、如图:函数![]() (
(![]() ≠0)与
≠0)与![]() 的图象交于A、B两点,过点A作AC垂直于
的图象交于A、B两点,过点A作AC垂直于![]() 轴,垂足为点C,则△BOC的面积为
。
轴,垂足为点C,则△BOC的面积为
。
19、如图:正方形ABCD中,过点D作DP交AC于点M、交AB于点N,交CB的延长线于点P,若MN=1,PN=3,则DM的长为 。
20、把一个半径为8cm 的圆片,剪去一个圆心角为800的扇形后,用剩下的部分做成一个圆锥的侧面,那么这个圆锥的高为 。
三、解答题:(本大题4个小题,共48分)下列各题解答时必须给出必要的演算过程或推理步骤。
21、(12分)已知![]() =3是方程
=3是方程![]() 的一个根,求
的一个根,求![]() 的值和方程其余的根。
的值和方程其余的根。
22、(12分)某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%。安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离。假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由。
23、(12分)在举国上下众志成诚抗击“非典”的斗争中,疫情变化牵动着全国人民的心,请根据下列疫情统计图表回答问题:

(1)上图是5月11日至5月29日全国疫情每天新增数据统计走势图,观察后回答:
①每天新增确诊病例与新增疑似病例人数之和超过100人的天数共有 天。
②在本题的统计中,新增确诊病例的人数的中位数是 ;
③本题在对新增确诊病例的统计中,样本是 ,样本的容量是 。
(2)下表是我国一段时间内全国确诊病例每天新增的人数与天数的频率统计表。(按人数分组)
| 分组 | 0-9 | 10-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-99 | 100以上 | 合计 |
| 频数 |
| 4 | 5 | 1 | 0 | 2 | 1 | 1 | 2 | 0 | 13 |
|
| 频率 | 0.275 | 0.1 |
| 0.025 | 0 | 0.05 | 0.025 | 0.025 | 0.05 | 0 |
| 1.000 |
①100人以下的分组组距是 。
②填写本统计表中未完成的空格。
③在统计的这段时期,每天新增确诊病例人数在80人以下的天数共有 天。
24、(12分)如图:已知⊙O1和⊙O2 相交于A、B两点,P是⊙O1上一点,PB的延长线交⊙O2 于点C,PA交⊙O2于点D,CD的延长线交⊙O1于点N。
(1)过点A作AE∥CN交⊙O1于点E,求证:PA=PE;
(2)连结PN,若PB=4,BC=2,求PN的长。

四、解答题:(本大题2个小题,共22分)下列各题解答时必须给出必要的演算过程或推理步骤。
25、(12分)已知抛物线![]() 与
与![]() 轴交于点A(
轴交于点A(![]() ,0)、B(
,0)、B(![]() ,0)两点,与
,0)两点,与![]() 轴交于点C,且
轴交于点C,且![]() <
<![]() ,
,![]() +2
+2![]() =0。若点A关于
=0。若点A关于![]() 轴的对称点是点D。
轴的对称点是点D。
(1)求过点C、B、D的抛物线的解析式;
(2)若P是(1)中所求抛物线的顶点,H是这条抛物线上异于点C的另一点,且△HBD与△CBD的面积相等,求直线PH的解析式。
26、(10分)电脑CPU蕊片由一种叫“单晶硅”的材料制成,未切割前的单晶硅材料是一种薄型圆片,叫“晶圆片”。现为了生产某种CPU蕊片,需要长、宽都是1cm 的正方形小硅片若干。如果晶圆片的直径为10.05cm。问一张这种晶圆片能否切割出所需尺寸的小硅片66张?请说明你的方法和理由。(不计切割损耗)

普通高中招生统一考试
数学试题参考答案及评分意见
一、选择题:(每小题4分,共48分)
CCBAD,CCABD,BC
二、填空题:(每小题4分,共32分)
13、![]() 14、
14、![]() 15、990 16、-1
15、990 16、-1
17、![]() ≥3
18、2
19、2
20、
≥3
18、2
19、2
20、![]()
三、解答题:(每小题12分,共48分)(除23小题外,其余各题的评分均为累计计分)
21、解:将![]() =3代入原方程得:
=3代入原方程得:![]() (1分)
(1分)
解得:![]() =-3 (4分)
=-3 (4分)
将![]() =-3代入原方程得:
=-3代入原方程得:![]() (5分)
(5分)
整理得:![]() (8分)
(8分)
解得:![]() =2,
=2,![]() =3
(10分)
=3
(10分)
经检验:![]() =2,
=2,![]() =3都是原方程的解。 (11分)
=3都是原方程的解。 (11分)
∴当![]() =3是方程的一个根时,
=3是方程的一个根时,![]() =-3,方程的另一个根为
=-3,方程的另一个根为![]() =2 (12分)
=2 (12分)
22、解:(1)设平均每分钟一道正门可以通过![]() 名学生,一道侧门可以通过
名学生,一道侧门可以通过![]() 名学生,(1分)由题意得:
名学生,(1分)由题意得:
![]() (4分)
(4分)
解得:![]() (7分)
(7分)
答:平均每分钟一道正门可以通过120名学生,一道侧门可以通过80名学生。(8分)
(2)这栋楼最多有学生4×8×45=1440(名)
拥挤时5分钟4道门能通过:![]() =1600(名)(10分)
=1600(名)(10分)
∵1600>1440
∴建造的4道门符合安全规定。 (12分)
23、(1)(共6分)① 7 (2分);② 26 (1分);③5月11至5月29日每天新增确诊病例人数(2分) 19 (1分)
(2)(共6分)每空位或每空格1分
① 10人 ;②11、40、0.125、0.325 ;③ 25 ;
24、(1)证明:连结AB (1分)
∵四边形AEPB是⊙O1的内接四边形
∴∠ABC=∠E (2分)
在⊙O2中,∠ABC=∠ADC
∴∠ADC=∠E (4分)
又∵AE∥CN
∴∠ADC=∠PAE
故∠PAE=∠E
∴PA=PE (6分)


(2)连结AN (7分)
四边形ANPB是⊙O1的内接四边形
∴∠ABC=∠PNA (8分)
由(1)可知∴∠PDN=∠ADC=∠ABC
∴∠PDN=∠PNA
又∠DPN=∠NPA
∴△PDN∽△PNA (10分)
∴![]() (11分)
(11分)
又∵在⊙O2中,由割线定理:PB·PC=PD·PA
∴![]() (12分)
(12分)
四、解答题:(共22分)
25、解:(1)由题意得: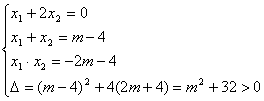
由①②得:![]() ,
,![]()
将![]() 、
、![]() 代入③得:
代入③得:![]()
整理得:![]()
∴![]() =2
=2 ![]() =7
(2分)
=7
(2分)
∵![]() <
<![]()
∴![]() <
<![]()
∴![]() <4
<4
∴![]() =7(舍去)
(3分)
=7(舍去)
(3分)
∴![]() =-4,
=-4,![]() =2,点C的纵坐标为:
=2,点C的纵坐标为:![]() =8
=8
∴A、B、C三点的坐标分别是A(-4,0)、B(2,0)、C(0,8) (4分)
又∵点A与点D关于![]() 轴对称
轴对称
∴D(4,0) (5分)
设经过C、B、D的抛物线的解析式为:![]() (6分)
(6分)
将C(0,8)代入上式得:![]()
∴![]() =1
=1
∴所求抛物线的解析式为:![]() (7分)
(7分)
(2)∵![]() =
=![]()
∴顶点P(3,-1) (8分)
设点H的坐标为H(![]() ,
,![]() )
)
∵△BCD与△HBD的面积相等
∴∣![]() ∣=8
∣=8
∵点H只能在![]() 轴的上方,故
轴的上方,故![]() =8
=8
将![]() =8代入
=8代入![]() 中得:
中得:![]() =6或
=6或![]() =0(舍去)
=0(舍去)
∴H(6,8) (9分)
设直线PH的解析式为:![]() 则
则
![]() (10分)
(10分)
解得:![]() =3
=3 ![]() =-10
=-10
∴直线PH的解析式为:![]() (12分)
(12分)
26、答:可以切割出66个小正方形。 (1分)
方法一:
(1)我们把10个小正方形排成一排,看成一个长条形的矩形,这个矩形刚好能放入直径为10.05cm 的圆内,如图中矩形ABCD。
∵AB=1 BC=10
∴对角线![]() =100+1=101<
=100+1=101<![]() (3分)
(3分)
(2)我们在矩形ABCD的上方和下方可以分别放入9个小正方形。

∵新加入的两排小正方形连同ABCD的一部分可看成矩形EFGH,矩形EFGH的长为9,高为3,对角线![]() <
<![]() 。但是新加入的这两排小正方形不能是每排10个,因为:
。但是新加入的这两排小正方形不能是每排10个,因为:
![]() >
>![]() (6分)
(6分)
(3)同理:![]() <
<![]()
![]() >
>![]()
∴可以在矩形EFGH的上面和下面分别再排下8个小正方形那么现在小正方形已有了5层。 (8分)
(4)再在原来的基础上,上下再加一层,共7层,新矩形的高可以看成是7,那么新加入的这两排,每排都可以是7个但不能是8个。
∵![]() <
<![]()
![]() >
>![]() (9分)
(9分)
(5)在7层的基础上,上下再加入一层,新矩形的高可以看成是9,这两层,每排可以是4个但不能是5个。
∵![]() <
<![]()
![]() >
>![]()
现在总共排了9层,高度达到了9,上下各剩下约0.5cm 的空间,因为矩形ABCD的位置不能调整,故再也放不下一个小正方形了。
∴10+2×9+2×8+2×7+2×4=66(个) (10分)
方法二:
学生也可能按下面的方法排列,只要说理清楚,评分标准参考方法一。
可以按9个正方形排成一排,叠4层,先放入圆内,然后:
(1)上下再加一层,每层8个,现在共有6层。
(2)在前面的基础上,上下各加6个,现在共有8层。
(3)最后上下还可加一层,但每层只能是一个,共10层。
这样共有:4×9+2×8+2×6+2×1=66(个)
 项目
项目