三角形单元达纲检测AA级

三角形单元达纲检测AA级

【同步达纲练习】

一、选择题(3分×10=30份)

1.三条线段a,b,c长度均为整数且a=3,b=5.则以a,b,c为边的三角形共有(　　)

A.4个　　　　  B.5个　　　　　 C.6个　　　　　  D.7个

2.一个三角形中，下列说法正确的是(　　)

A.至少有一个内角不小于90°　　 B.至少一个内角不大于30°

C. 至少一个内角不小于60°　　　D. 至少一个内角不大于45°

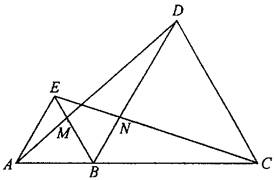
图3.AA-1

3.如图3.AA-1，B为AC上一点，在AC同侧作等边△ABE和等边△BCD,则下列式子中错误的是(　　)

A.△ABD≌△EBC　　　　　　  B.△NBC≌△MBD

C.∠BDA=∠BCE　　　　　　　 D.△ABE≌△BCD

4.△ABC中，AB=7，AC=5，则中线AD之长的范围是(　　)

A.5＜AD＜7　　　B.1＜AD＜6　　　C.2＜AD＜12　　　 D.2＜AD＜5

5.下列各组中的比为三角形三边之比，其中，不能构成直角三角形的是(　　)

A.3∶4∶5  　　　B.5∶12∶13　　　C.2∶4∶5　　　　 D.7∶24∶25

6.△ABC中，∠A=40°,高BD和CE交于O，则∠COD为(　　)

A.40°或140°　　B. 50°或130°　 C. 40°　　　　　 D. 50°

7.△ABC中，AB=AC，D为BC延长线上一点，则下列不等式一定成立的是(　　)

A. ∠ACB＞∠ACD　　　　　　　　 B. ∠ACB≥∠ACD

C. ∠ACB≤∠ACD　　　　　　　　 D. ∠ACB＜∠ACD

8.直角三角形周长为2+，斜边中线为1,则该三角形面积为(　　)

A.　　　　　　  B.　　　　　  C.　　　　　　 D.1

9.在Rt△ABC中，∠C=90°,高CH和中线CM三等分∠ACB.若△CHM面积为k,那么△ABC的面积是(　　)

A.3k　　　　　　　B.4k　　　　　　 C.3k　　　　  D.4k

10.△ABC中，∠A=45°, ∠B=30°,BC=8,则AC值为(　　)

A.4　　　　　　　 B.4　　　　　 C.4　　　　　 D.4

二、填空(3分×10=30分)

1.若三角形三边长为3、2a-1、8，则a的取值范围是　　　　  .

2.如果等腰三角形两外角比为1∶4则顶角为　　　.

3.如图3.AA-2, ∠A=40°, ∠C=70°, ∠1=∠2, ∠3=∠4,则∠F=　　　　.

　　　　

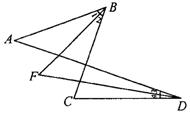
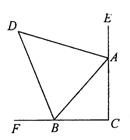
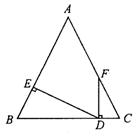
　　　　 图3.AA-2　　　　　　　　  图3.AA-3　　　　　　　 图3.AA-4

4.等腰三角形两边比为1∶2,周长为50，则腰长为　　　　 .

5.等腰三角形底边长为20，腰上的高为16.则腰长为　　　　 .

6.如图3.AA-3,△ABC中，∠C=90°,E在CA延长线上，F在CB延长线上，∠EAB和∠FBA的角平分线交于D，则∠D=　　　　  .

7.一个三角形的三条角平分线交点，三条中线的交点，三条高的交点三点共点，则该三角形一定是　　　　 .

8.“有两条边对应相等的两个直角三角形全等”这个命题是一个　　　　命题(添“真”“假”).

9.直角三角形周长和面积都等于30，则斜边长为　　　　.

10.如图3.AA-4，△ABC中，AB=AC，D在BC上，FD⊥BC交AC于F，DE⊥AB于E.若∠EDF=70°,则∠AFD=　　　.

三、解答题(第1-5小题每题6分，第6小题10分)

1.如图3.AA-5,AC∥DF，AB=DE，∠B=∠E，BC=EF.求证AF=CD.

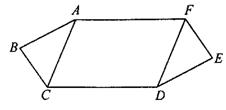
图3.AA-5　　　　　

2.如图3.AA-6.求证AB+BC+CD+DA＞AC+BD.

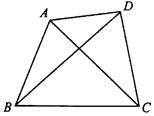
图3.AA-6　　　

3.如图3.AA-7，△ABC中，∠C=90°,AC=BC,l为过C的任一直线，AD⊥l于D，BE⊥l于E.求证DE=AD+BE.

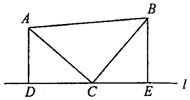
图3.AA-7　　　　

4.如图3.AA-8,，∠1=∠2,AD=DC,求证∠A+∠C=180°.

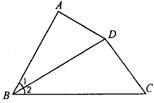
图3.AA-8

5.如图3.AA-9,△ABC中AB=AC，P为BC上一点.求证AB²-AP²=BP·CP

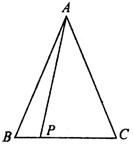
图3.AA-9　　

6.如图3.AA-10，△ABC中，∠B=60°,角平分线AD、CE交于O.

(1)求证AE+CD=AC

(2)若∠AEC=75°,求的值.

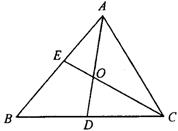
图3.AA-10　　

参考答案

【同步达纲练习】

一、1.B　2.C  3.D　4.B　5.C  6.A　7.D　8.C  9.B　10.B

二、1.3＜a＜6  2.140°  3.55°  4.20　5.　6.45°　7.等边三角形　8.假　9.13　10.160°

三、1.∵AB=DE　∠B=∠E  BC=EF　∴△ABC≌△DEF　∴AC=DF.

连AD，AC∥DF  ∴∠CAD=∠FDA　AD=AD　AC=DF

∴△ACD≌△DFA　∴AF=CD

2.AB+AD＞BD　CB+CD＞BD　AB+BC＞AC　AD+CD＞AC.

∴2(AB+BC+CD+DA)＞2(AC+BD)　∴AB+BC+CD+DA＞AC+BD.

3.∵∠C=90° ∴AC⊥BC　又AD⊥AC, ∴∠ACD=∠CBE,∠D=∠E=90° 又AC=BC　∴△ACD≌△CBE　∴AD=CE　CD=BE.

∴DE=AD+BE.

4.作DE⊥BA交BA延长线于E，DF⊥BC于F，  ∵∠1=∠2　∴DE=DF又DA=DC

∴Rt△DAE≌Rt△DCF.　∴∠C=∠DAE  ∴∠A+∠C=180°

5.作AD⊥BC于D.AB=AC　∴BD=DC.

AB²-AP²=(BD²+AD²)-(PD²+AD²)=(BD+PD)(BD-PD)=(BD-PD)(CD+PD)=BP·CP.

6.(1) ∠B=60°　∴∠AOC=90°+×60°=120°，∠AOE=60°

在AC上取AF=AE.易证△AEO≌△AFO ∴∠AOF=∠AOE=60°∠FOC=∠COD=60°

∠FCO=∠DCO　OC=OC

∴△DOC≌△FOC　∴DC=CF.　∴AE+CD=AC.

(2)作DM⊥AC于M　∵∠AEC=75° ∴∠ECB=15°　∠ACB=30°　∠BAC=90°

∠DAC=45°  ∴DC=2DM  DM=AM.AM=DC

MC=DC　∴AC=DC　∵AE+DC=AC

∴AE=AC-DC=DC.

=+1.