三角形单元达纲检测A级
【同步达纲练习】
一、判断(2分×5=10分)
( )1.△ABC中，D为BC的中点，则直线AD为△ABC的中线.
( )2.三角形的外角大于内角.
( )3.有两角及一边对应相等的两个三角形全等.
( )4.等腰三角形的一边上的高、对角平分线、该边中线三线合一.
( )5.有一个外角为135°的直角三角形是等腰直角三角形.
二、选择(3分×10=30分)
1.底为10的等腰三角形腰长为b，则b的取值范围是( )
A.0＜b＜5 B.0＜b＜10 C.b＞10 D.b＞5
2.三角形两内角比为6∶7,第三个角的外角为130°,则最小的内角度数为( )
A.40° B.50° C.60° D.70°
3.△ABC和△A′B′C′中，AB=A′B′ BC=B′C′，则还需下列条件中的哪一个，可得两三角形全等( )
A.∠A=∠A′ B. ∠B=∠B′
C. ∠C=∠C′ D.BC边上的高与B′C′边上的高相等
4.三条线段a＜b＜c，则只需满足下列哪个条件，以a,b,c为边就可构成三角形( )
A.a+b＞c B.a+c＞b C.b+c＞a D.a-b＜c
5.直角三形两直角边的比为24∶7,则周长与最短边的比为( )
A.7:1 B.8∶1 C.25∶7 D.31∶7
6.等腰三角形腰上的高与底边的夹角为m°则顶角度数为( )
A.m° B.2m° C.(90-m)° D.(90-2m)°
7.△ABC中，∠A、∠B、∠C的对边分别为a、b、c，若∠A∶∠B∶∠C=1∶2∶3则( )
A.a=2b B.a2=3b2 C.c2=4b2 D.b2=3a2
8.边长为2的等边三角形的角平分线长为( )
A.1
B.
C.
D.
9.D为△ABC的边BC的中点，且AD=DB=DC，则△ABC一定为( )
A.等腰三角形 B.等边三角形
C.等腰直角三角形 D.直角三角形
10.△ABC中，AB=AC，P为BC上任一点，则( )
A.AB≥AP B.AB≤AP C.AB＞AP D.AB＜AP
三、填空(3分×10=30分)
1.等腰直角三角形斜边长为3,则周长为
.
2.三角形三个外角比为3∶4∶5,则三个内角比为 .
3.△ABC中∠A=50°,角平分线BD、CE交于O，则∠BOC= .
4.等腰三角形周长为48cm,腰比底边长9cm，则三边长为 .
5.△ABC中，AB=AC=6，∠A=60°,BD为高，则BD= .
6.△ABC的三边长为5、12、13，则最长边上的高为 .
7.等边三角形的对称轴有 条.
8. ∠MON=70°,P为形内一点，且到两边距离相等，则∠MOP= .
9.△ABC中，∠A=∠B=2∠C，则∠C= .
10.等腰三角形一边为，另一边为
，则它的周长是
.
四、解答题(共30分)
1.D、E为△ABC的边BC上两点且AD=AE，BE=DC，求证AB=AC(图3.A-1)(5分)
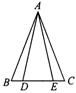
图3.A-1
2.如图3.A-2,CA=CB,DF=DB,AE=AD,求∠A的度数.(5分)
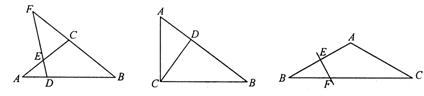
图3.A-2 图3.A-3 图3.A-4
3.直角三角形ABC中，∠C=90°,CD⊥AB于D.AC=12，BC=16，求AD.(图3.A-3)(5分)
4.△ABC中，AB=AC，∠B=30°,AB中垂线交AB于E，BC于F，(图3.A-4)，求证：EF=
BC.(6分)
5.已知△ABC中，∠A=90°，AB=AC，M为AC中点，AE⊥BM于E.延长AE交ＢＣ于Ｄ(图3.A-5)，求证∠ＡＭＢ＝∠ＣＭＤ.(9分)
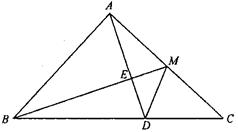
图3.A-5
参考答案
【同步达纲练习】
一、× × √ × √
二、D B B A B，A D B D C
三、1.6+3 2.3∶2∶1 3.115° 4.10,19,19 5.3 6.
7.三 8.35° 9.36°
10.2+或2
.
四、1.∵BE=DC ∴BD=CE 作AF⊥BC于F ∵AD=AE ∴DF=EF
∴BF=CF ∴AB=AC.
2.∵CA=CB DF=DB AE=AD ∴∠A=∠B=∠F.
∠EDA=∠DEA=2∠B=2∠A ∴5∠A=180° ∠A=36°
3.AC=12 BC=16
∴AB=20 CD=
=
12.AD2=AC2-CD2=122-(12)2=122×(
)2 ∴AD=
4.连AF，EF为中垂线 ∴AF=BF.AB=AC ∠B=30° ∴∠BAC=120° ∠C=30°
∠BAF=30° ∠FAC=90° AF=
FC，EF=AF.
BF=FC，BF=
BC，AF=BC ∴EF=BC.
5.作∠BAC的平分线交BM于N，AE⊥BM，BA⊥AC ∴∠ABN=∠CAE，
∠BAN=∠C=45° AB=AC ∴△BAN≌△ACD. ∴AN=CD
∠NAM=∠C=45° AM=MC ∴△NAM≌△DCM ∴∠AMB=∠CMD