第14课 正比例、反比例、一次函数
〖知识点〗
正比例函数及其图像、一次函数及其图像、反比例函数及其图像
〖大纲要求〗
1．理解正比例函数、一次函数、反比例函数的概念；
2．理解正比例函数、一次函数、反比例函数的性质；
3．会画出它们的图像；
4．会用待定系数法求正比例、反比例函数、一次函数的解析式
内容分析
1、一次函数
（1）一次函数及其图象
如果y=kx+b（K，b是常数，K≠0），那么，Y叫做X的一次函数。
特别地，如果y=kx（k是常数，K≠0），那么，y叫做x的正比例函数
一次函数的图象是直线，画一次函数的图象，只要先描出两点，再连成直线
（2）一次函数的性质
当k>0时y随x的增大而增大，当k<0时，y随x的增大而减小。
2、反比例函数
(1) 反比例函数及其图象
如果
,那么，y是x的反比例函数。
反比例函数的图象是双曲线，它有两个分支，可用描点法画出反比例函数的图象
（2）反比例函数的性质
当K>0时，图象的两个分支分别在一、二、三象限内，在每个象限内， y随x的增大而减小；
当K<0时，图象的两个分支分别在二、四象限内，在每个象限内，y随x的增大而增大。
3.待定系数法
先设出式子中的未知数，再根据条件求出未知系数，从而写出这个式子的方法叫做待定系数法可用待定系数法求一次函数、二次函数和反比例函数的解析式
〖考查重点与常见题型〗
1． 考查正比例函数、反比例函数、一次函数的定义、性质，有关试题常出现在选择题中
2． 综合考查正比例、反比例、一次函数的图像，习题的特点是在同一直角坐标系内考查两个函数的图像，试题类型为选择题
3． 考查用待定系数法求正比例、反比例、一次函数的解析式，有关习题出现的频率很高，习题类型有中档解答题和选拔性的综合题
4． 利用函数解决实际问题，并求最值，这是近三年中考应用题的新特点。
考查题型
1．若函数y＝（m＋1）xm2+3m+1是反比例函数，则m的值是（ ）
(A) m＝－1 （B）m＝-2（C）m＝2或m＝1 （D）m＝－2或m＝－1
2．已知一次函数y＝（m＋2）x＋（1－m），若y随x的增大而减小，且该函数的图像与x轴的交点在原点的右侧，则m的取值范围是（ ）
（A）m>－2 （B）m<1 （C）－2<m<－1 （D）m<－2
3．函数y＝与y＝kx＋1（k≠0）在同一坐标系内的图像大致为图中的（ ）
y
y
y
y
x
x
x
x
A B C D
4．已知一次函数的图像是一条直线，该直线经过(0,0)，(2,－a)，(a,－3)三点，且函数值随自变量x值的增大而减小，则此函数的解析式 。
5．一次函数y＝2x－3在y轴上的截距是
6．对于函数y＝－，当x>0时，y随x的增大而
7．如果直线y＝2x＋m不经过第二象限，那么实数m的取值范围是
8．若双曲线y＝（m－1）x－1在第二、四象限，则m的取值范围是
9．已知直线y＝ｘ＋ｂ被两坐标轴截取的线段长为5，求此直线函数解析式。
10．已知一次函数y＝ｋx＋2ｂ＋3的图象经过点（－1，－3），ｋ是方程
ｍ2－3ｍ＝10的一个根，且Y随ｘ的增大而增大，求这个一次函数解析式。
考点训练：
1． y= x 的图象是一条过原点及点(-3,3)的直线
2．一次函数y=kx+b 的图象经过P(1,0) 和Q(0,1)两点，则k= ,b= .
3．正比例函数的图象与直线y= -x+4平行，则该正比例函数的解析式为 ，
该正比例函数y 随x的增大而 .
4．已知y-2与x成正比例，且x=2时,y=4,则y与x之间的函数关系是 ，若点(m,2m+7), 在这个函数的图象上，则m =
5． 函数y=(m-4)xm2-5m-5的图象是过一、三象限的一条直线，则 m =
6．函数y=(k≠0)的图象经过点(,3),则k= ,当x>0时，y随着x的增大而
7．如果一次函数y=kx+b和反比例函数y=的图象都经过(-2,1)点，则b的值是
8．已知一次函数y=kx+b的y随x的增大而减小，那么它的图象必经过 象限。
9．已知函数y= -2x-6。（1）求当x= -4时，y的值，当y= -2时，x 的值。
（2）画出函数图象；
（3）求出函数图象与坐标轴的两个交点之间的距离；
（4）如果y 的取值范围-4≤y≤2,求x的取值范围.
10.已知z与y-成正比例,x与成反比例，（1）证明：y是x的一次函数；(2)如果这个一次函数的图象经过点(-2,3)，并且与x、y轴分别交于A、B两点。求两 点的坐标。
＊11．已知函数y=的图象上有一点P（ｍ，ｎ），且ｍ，ｎ关于ｔ的方程ｔ2－4ａｔ＋4ａ2－6ａ－8＝0的两个实数根，其中ａ是使方程有实数根的最小整数，求函数y=的解析式，
解题指导
1.函数y= - x的图象是一条过原点(0,0)及点(2, )的直线，这条直线经过第
象限，y随的增大而
2.已知一次函数y= - x+2,当x= 时,y=0;当x 时y>0; 当x 时y<0.
3.若一次函数y1=kx-b图象经过第一、三、四象限，则一次函数y2=bx+k的图象经过第 象限。
4.直线y1=k1x+b1和直线y2=k2x+b2相交于y轴上同一点的条件是 ；这两直线平行的条件是
5.过点（0，2）且与直线y= - x平行的直线是 。
6.y与3x+2成正比例，比例系数是4，则y与x的函数关系式是 。
7.等腰三角形的周长为30cm，它的腰长为ycm与底长xcm的函数关系式是 。
8.y= x -1 的图象是一条过点（，- ）的双曲线，在它的图象所在的每一个象限内，y随x的增大而 。
9.把直线y= －x -2向上平移2个单位，得到直线 ，
把直线y= - x -2向 平移 个单位，得到直线y= - (x+4)
10.写出满足下表的一个一次函数的关系式
| x | - 1 | 2 | 5 |
| y | 7.5 | 6 | 4.5 |
11.直线y=kx+b经过点（0，3）,且与两坐标轴构成的直角三角形的面积是6，求其解析式。
12．已知反比例函数y=(k>0)的图象上的一点P,它到原点O的距离OP=2,PQ垂直于y轴,垂足为Q.若△OPQ的面积为4平方单位，求：（1）点P的坐标；（2）这个反比例函数的解析式.
独立训练（一）：
1．函数y= - 是 函数，这个函数的图象位于第 象限。
2．对函数y= - 当x>0时，y随x的增大而 。
3．反比例函数y=的图象上有一点P，它的横坐标m与纵坐标n是方程t2-4t-2=0的两个根，则k=
4．如图，P为反比例函数y=的图象上的点，过P分别向
x轴和y轴引垂线，它们与两条坐标轴围成的矩形面积为2，
这个反比例函数解析式为 。
5．反比例函数y=(a-3)x
-2a-4的函数值是4时，它的自变量x的值是
。
6．一次函数y=kx+b与反比例函数y=的图象的两个交点的横坐标为和 -1，则一次函数y=
7．一次函数y=kx+b过点（-2，5），且它的图象与y轴的交点和直线y=－x+3与y轴的交点关于x轴对称，那么一次函数的解析式是
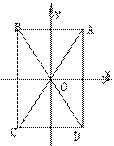
8．如图，在矩形ABCD中，已知AB=2，BD=6，对角线AC
和BD相交于O，以O为原点分别以平行于AB和AD的直线为
轴和轴建立平面直角坐标系，则对角线AC和BD的函
数表达式分别为 。
9．求直线y=3x+10,y= -2x-5与y轴所围成的三角形的面积。
10．如图，一次函数y=k1x+b的图象过一、三、四象限，且
与双曲线y=的图象交于A、B两点，与y轴交于C点，且
A（x1，y1）是∠XOA终边上一点。
（1） 
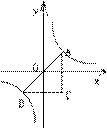tg∠XOA=，原点到A点的距离为，求A点的坐标；
（2）在（1）的条件下，若S△AOC=b2－6，求一次函数的解析式。
独立训练（二）：
1. 如图,A、B是函数y=的图象上关于原点O对称的任意两点，AC
平行于y轴，BC平行于x轴，△ABC的面积S，则（ ）
（A）S=1 （B） 1<S<2 （C） S=2 （D） S>2
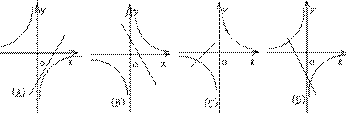2．函数y=k1x+b(k1b<0)与y=(k2<0)在同一坐标系中的图象大致是（
）
 |
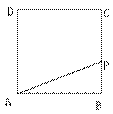3．在边长为的正方形ABCD的边BC上，有一点P从
B点运动到C点，设PB=x，图形APCD的面积为y，
写出y与自变量x的函数关系式，并且在直角坐标系
中画出它的图象
4.已知y=y1+y2,y1与x2成正比例，y2与x成反比例，并且当x=1时,y=1,当x=3时,y=-17,求x=-1时,y的值
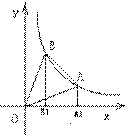5．如图，在y= (x>0)反比例函数的图象上有不重合的两点
A、B，且A点的纵坐标是2，B点的横坐标为2，BB1和AA1
都垂直于轴，垂足分别为B1和A1，（1）求A点横坐标；
（2）求S△
（3）当OB=2时，求S△OBA
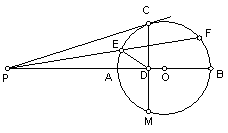6．如图已知AB是⊙O的直径，P是BA延长线上一点，
PC切⊙O于C，PA＝6，PEF是⊙O的割线，设PE＝ｘ，
PF＝y，弦CM⊥AB于D，且AD：DB＝1：2，
求ｙ与ｘ之间的函数关系式，
并求出自变量ｘ取值范围。