高级中等学校招生统一数学考试试卷
（）
一、填空题（每小题2分，共24分）
1．计算：
________________.
2．函数
的自变量x的取值范围是________________________.
3．当x=__________时，代数式
的值为零.
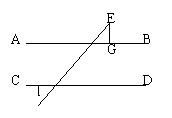
4．如图1，AB//CD，EG⊥AB，垂足为G，若∠1=50°，
则∠E=_____________度.
5．若关于x的一元二次方程
有两个实数根，则符合条件的一组m、n的实数值可以是m=______,n=________.
6．若
，计算
=___________________.
7. 某商品的进价是500元，标价为750元，商店要求以不低于5%的售价打折出售，售货员最低可以打__________折
8．某学校需修建一个圆心角为60°，半径为12米的扇形投掷场地，则该扇形场地的面积约为_____________米2.（π取3.14）
9．如果
那么a+b的值为____________________.
10．一元二次方程
的两根之和为2a-1，则两根之积为_________.
|
可以分解为________________________________.
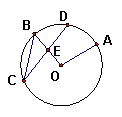
12．如图2，点A、B、C、D是圆O上四点，且点D
是弧AB 的中点，CD交OB于E，∠AOB=100°，
∠OBC=55°，则∠OEC=__________度.
二、选择题（每小题3分，共15分）
13．已知数轴上的A点到原点的距离为2，那么在数轴上到
A点的距离是3的点所表示的数有【 】
（A）1个 （B）2个 （C）3个 （D）4个
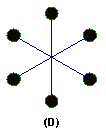
14．如图3所示的图中，既是轴对称又是中心对称图形的是【 】
15．三角形两边的长分别是8和6，第3边的长是一元二次方程
的一个实数根，则该三角形的面积是【 】
（A）24 （B）24或
（C）48 （D）
16．用两个全等的直角三角形拼下列图形：（1）平行四边形（不包含菱形、矩形、正方形）；（2）矩形；（3）正方形；（4）等腰三角形，一定可以拼成的图形是【 】
（A）（1）（2）（5） （B）（2）（3）（5） （C）（1）（4）（5） （D）（1）（2）（3）
17．如图4，函数图象①、②、③的表达式应为【 】
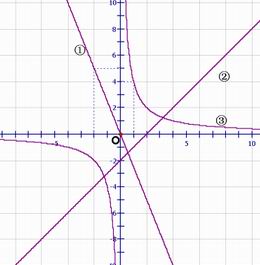（A）
，
，
（B）
， 
，
（C），
，
（D），，
三、（第18、19小题各5分，第20、21小题各6分，共22分）
18．计算
19．如图5，木工师傅要把一块矩形木板ABCD的四个角锯成半径为5cm，且与两边相切的圆弧形，请你帮助师傅设计一种方案，并在木板上把一个角的圆弧线画出来（保留画图痕迹，写出画法）.
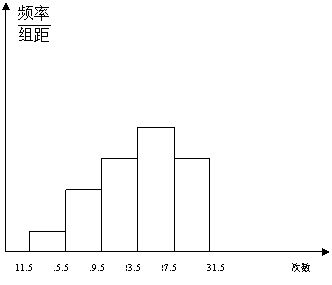
20．图6是某学校初三年级部分学生做引体向上的成绩进行整理后，分成五组，画出的频率分布直方图.已知从左到右前四个小组的频率分别是0.05、0.15、0.25、0.30，第五小组的频数是25，根据已知条件回答下列问题：
（1）第五小组的频率是多少？
（2）参加本次测试的学生总数是多少？
（3）如果做20次以上为及格（包括20次），求此次测试及格的人数是多少.
 |
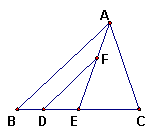
21．已知：如图7，△ABC（AB≠AC）中，D、E在BC上，且DE=EC，过D作DF//BA，交AE于点F，DF=AC.
求证：AE平分∠BAC.
四、（每小题7分，共14分）
22．解方程
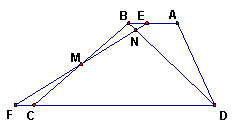
23．已知：如图8，在梯形ABCD中，AB//CD，AB=1/3CD，E是AB上一点，AE=2BE，M是腰BC的中点，连结EM并延长交DC的延长线于点F，连结BD交EF于点N。
求证：BN：ND=1：10。
五、（8分）
24.在抗击“SARS”的过程中，某厂甲、乙两工人按上级指示同时做一批等数量的防护服，开始时，乙比甲每天少做3件，到甲乙两人都剩下80件时，乙比甲多做了2天，这时，甲保持工作效率不变，乙提高了工作效率后比原来每天多做5件，这样甲乙两人同时完成任务。求甲乙两人原来每天各做多少防护服。
六、（8分）
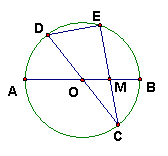
25.已知：如图9，在半径为4的⊙O中，AB、CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM>MC，连结DE ，DE=
.
（1）求EM的长；
（2）求sin∠EOB的值.
七、（9分）
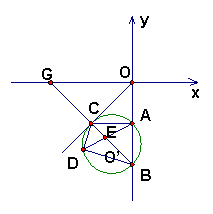
26．已知：如图10，在平面直角坐标系中，半径为
的⊙O’与y轴交于A、B两点，与直线OC相切于点C，∠BOC=45°，BC⊥OC，垂足为C.
（1）判断△ABC的形状；
（2）在弧BC上取一点，连结DA、DB、DC，DA交BC于点E.
求证：BD·CD=AD·ED；
（3）延长BC交x轴于点G，求经过O、C、G三点的二次函数的解析式.
