第23课时 梯形
知识点：梯形、等腰梯形、直角梯形、等腰梯形的性质和判定、四边形的分类
大纲要求：
1． 掌握梯形、等腰梯形、直角梯形的概念，等腰梯形的性质和判定；
2． 四边形的分类和从属关系。
考查重点与常见梯形
1． 
考查梯形的判定、性质及从属关系，在中考题中常以选择题或填空题出现，也常以证明题的形式出现。如：
（A） 圆内接平行四边形是矩形；
（B） 一组对边平行另一组对边不平行的四边形一定是梯形；
（C） 顺次连结等腰梯形各边中点构成的四边形是菱形；
（D） 两条对角线互相垂直且相等的四边形是正方形。
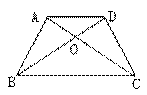
2． 求梯形的面积、线段的长，线段的比及面积的比等，在中考题中常以选择题或填空题出现，也常以证明题的形式出现。 如：如图梯形ABCD中，AD∥BC，AC、BD交于O点，S⊿AOD：S⊿COB＝1：9，则S⊿DOC：S⊿BOC＝
3． 梯形与代数中的方程、函数综合在一起， 如在直角梯形ABCD中，AD∥BC，AB⊥AD，AB＝10，AD、BC 的长是x2-20x+75=0方程的两根，那么以点D为圆心、AD长为半径的圆与以C圆心，BC为半径的圆的位置关系是 。
预习练习
1． 梯形两底的差是4，中位线长是8，则上底是 ，下底长是 。
2． 等腰梯形有一个角是60°，上下底长分别是2cm和6cm，则腰长为 。
3． 若梯形的中位线被它的两条对角线三等分，则梯形的上底a与下底b(a<b)的比是（ ）
（A） （B） （C） （D）
4． 直角梯形一腰长10cm，则一条腰与底边所成的角是30°，则另一腰长为 cm。
5． 等腰梯形ABCD中，AD∥BC，（1）如果延长BA和CD相交于E，则
EA＝ ，（2）如果作AF∥DC交BC于F，则⊿ABF是 三角形，四边形ADCF是 形。（3）如果作AG⊥BC于G，DH⊥BC于H，则BG＝ ＝ ，（4）如果作DK∥AC交BC的延长线于K，则DK＝ ＝ 。
考查训练：
1．顺次连结等腰梯形四边中点所得的四边形是（ ）
（A）矩形 （B）菱形 （C）等腰梯形 （D）正方形
2．梯形上底4，下底为6，则中位线夹在两对角线间的线段长为（ ）
（A）1 （B）2 （C）3 （D）4
3．四边形ABCD的四个角之比∠A：∠B：∠C：∠D＝1：2：2：3，则四边形是（ ）
（A）平行四边形 （B）等腰梯形 （C）直角梯形 （D）非直角、等腰梯形
4．梯形中位线长为15，一条对角线把它分成2：3，则梯形较长底边长是（ ）
（A）9 （B）12 （C）18 （D）20
5．梯形的面积为16cm2，高为4cm，它的中位线长为 cm.
6． 梯形ABCD中，AD∥BC，过D作DE∥AB交BC于E，梯形周长为53cm，AD＝7cm，则CDE的周长为 cm。
7． 等腰梯形ABCD中，AB∥CD，AB：CD＝1：2，中位线长是6cm，高8cm，则AB＝ cm，CD＝ cm，AD＝ cm，
8． 梯形ABCD中，∠A＝90°，AD∥BC，连BD，⊿DBC是等边三角形，⊿DBC的周长为27，则AD的长为 。
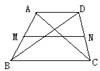
9． 
已知在梯形ABCD中，AB∥CD，AD＝BC，E是AB的中点，求证：ED＝EC
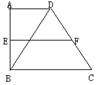
10.如图在直角梯形ABCD中，AD∥BC，∠A＝90°，中位线EF长为3cm，
⊿BDC为等边三角形，求梯形的两腰AB、DC的长及梯形的面积。
解题指导：
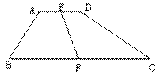
1． 如图，梯形ABCD中AD∥BC，对角线AC⊥BD，且AC＝2mn，
BD＝m2-n2(m>n>0)，求梯形中位线MN的长
 |
2． 如图，梯形ABCD中，AD∥BC，∠ B＋∠ C＝90°，E、F
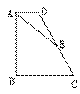分别是AD、BC的中点，求证：EF＝（BC－A
3． 在梯形ABCD中，AD∥BC，AB＝AD＋BC，E为CD中点，
求证：AE平分∠ DAB。
 |
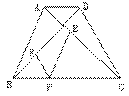4． 如图ABCD是等腰梯形，AB∥DC，AD＝BC。P是CD上任意一点，
过点P作AD，BC的平行线，分别交对角线AC，BD于点E、F，
求证：PE＋PF＝AD。
5． 
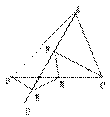如图，过⊿ABC的顶点A，任作一条直线AD，作BE⊥AD，CF⊥AD，E、F为垂足，M是BC的中点，求证：ME＝MF。
独立训练：
1．等腰梯形的下底是上底的3倍，上底与高相等，则下底角的度数为（ ）
（A）30 ° （B）45° （C）60° （D）75°
2．若梯形ABCD中，AB∥DC，AB＝5，BC＝3，∠BCD＝45°，∠CDA＝60°，则DC等于（ ）
（A）7＋2 （B）8 （C）8＋ （D）8＋3
3．若梯形的两条对角线分中位线为三等分，则梯形的上、下底之比为（ ）
（A）1：3 （B）2：3 （C）3：5 （D）1：2
4． 已知直角梯形的高为h，中位线长为m。一个底角为150°，则梯形的周长为 .
5． 等腰梯形的两底长为4cm和10cm，一底角为45°， 则它的面积为
6． 
如图直角梯形ABCD中，AD∥BC，∠ABC＝90°，
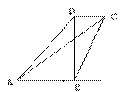AD：BC＝1：4，则BD：AC＝
7． 如图，梯形ABCD中，AB∥DC，对角线BD⊥AB，已知两底
与高的和为16cm，梯形面积为32cm2，求AC的长。
8． 
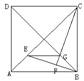如图，点E在正方形ABCD的对角线AC上，CF⊥BE交BD于点G，F是垂足，求证：四边形ABGE是等腰梯形。
9． 
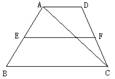如图，梯形ABCD中，AD∥BC，BD为对角线，S⊿ADB：S⊿DBC＝3：7，求中位线EF将梯形分成的两部分面积之比。