第21课 直角三角形
〖知识点〗
直角三角形的性质和判定、逆命题和逆定理、勾股定理及逆定理、角平分线的性质、线段的中垂线及其性质
〖大纲要求〗
了解逆命题和逆定理的概念；掌握直角三角形中两锐角互余、斜边上的中线等于斜边的一半及30°角所对的直角边等于斜边的一半等性质，掌握勾股定理及其逆定理，并能运用它们进行简单的论证和计算；掌握角平分线的性质定理及其逆定理，线段中垂线性质定理及其逆定理。
〖考查重点与常见题型〗
直角三角形性质及其判定的应用，角平分线性质定理及其逆定理，线段中垂线的性质定理及其逆定理的应用，逆命题的概念，中考题中多为选择题或填空题，有时也考查中档的解答题，如：
（1） 在直角三角形中，已知一条直角边的长为6，斜边上的中线长为5，则另一条直角边的长为
（2） 命题“平行四边形的对角线互相平分”的逆命题是
（3） 在△ABC中，如果∠A－∠B＝90°，那么△ABC是（ ）
(A)直角三角形(B)锐角三角形(C)钝角三角形(D)锐角三角形或钝角三角形
〖预习练习〗
1．直角三角形的两个锐角的平分线所交成的角的度数是（ ）
（A） 45° （B）135° （C）45°或135° （D）以上答案都不对
2.如图Rt△ABC，∠C＝90°，CD⊥AB，CE是AB上的中线，
∠ACD：∠BCD＝3：1，若CD＝4cm，则ED是（ ）
C
（A）
2cm （B）4cm （C）3cm （D）5cm
3．等腰直角三角形中，若斜边和斜边上的高的和是6cm， A B
则斜边长是 cm E D
4.三角形三个角的度数之比为1：2：3，它的最大边长等于16cm，则最小边长是 cm A
5.如图，△ABC中，AB＝AC，∠BAC＝120度，AD⊥AC，
DC＝5，则BD＝
6.AD是Rt△ABC斜边上的高，已知AB＝5cm，BD＝3cm ，
B D C
那么BC＝ cm
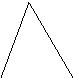7.如图，△ABC中，AB＝AC，DE是AB的中垂线，
A
△ 
BCE的周长为14cm, BC＝5cm，求AB的长。
D
E
B
C
考点训练：
1. 如果三角形中有一条边是另一条边是2倍,并且有一个角是30°,那么这个三角形是（ ）
(A)
直角三角形 (B)锐角三角形 (C)钝角三角形 (D) 图形不能确定
2.如图,RtΔABC中,∠BCA=90°, ∠A=30°CD⊥AB于D,DE⊥BC于E,
则AB:BE的值为( )
(A) 8 (B) 4 (C) (D) 3.5
3.等腰三角形一腰上的高与底边所成的角等于( )
(A) 顶角的2倍 (B) 顶角的一半 (C) 顶角 (D) 底角的一半
4.在直角三角形中,两锐角的平分线相交成钝角的度数是 .
5.直角三角形中,一条直角边比斜边上的中线长1厘米,如果斜
边长是10厘米, 则两直角边长是 .
6.已知:如图,在ΔABC中,AB>AC, D点在AB上,
AD=AC,AM⊥CD于M,E为BC的中点,若AB=16,AC=10,
则EM的长为
7.有一个角为30°的等腰三角形,若腰长为4,则腰上的高是 ,
面积是
.
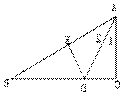
8.如图,在RTΔABC中, 斜边AB的中垂线DE 交BC于D,连结AD,
若∠1:∠2=2:5,求∠B、∠BAC的度数.
 |
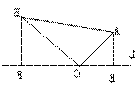9.如图,在ΔABC中, ∠BCA=90°,且AC=BC,
直线L过C点,AE⊥L于E,
BF⊥L于F. 求证:EF=AE+BF
 |
解题指导
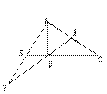
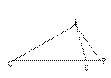
1. 如图,在ΔABC中, ∠ABC=2∠C,AD⊥BC于D,E是AC中点,ED的
延长线与AB的延长线交于点F,求证:BF=BD
 |
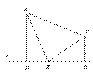
2．如图,在ΔABC中,∠B=40°, ∠C=20°, AD⊥CA于A, 交BC于D,
求证:CD=2AB
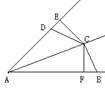
3．如图,AB⊥a于B,DC⊥a于C,∠BMA=75°, ∠DMC=45°,AM=DM,
求证:AB=CB
 |
4．如图,在四边形ABCD中,BC=DC,AC平分∠BAD,CE⊥AB,
CF⊥AD,E、F为垂足,若AB=21,AD=9,BC=DC=10,求AC的长.
独立训练:
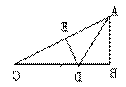
1. 
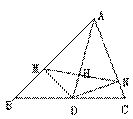如图,在ΔABC中,AD是∠BAC的平分线,DM⊥AB于M,DN⊥AC于N,
连接MN,则图中等腰三角形有 个,直角三角形有 个
 |
2. 如图,在RTΔABC中, ∠B=90°,
AD为BC边中线,DE⊥AC于E,
则:AB2+EC2 AE2
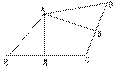
3. 已知:如图,AD∥BC,F是AB中点,DF交CB延长线于点E,CE=CD,则图中与∠ADE相等的角有 , 与∠ADE互余的角有 .
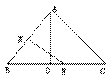
4. 已知:如图,在四边形ABCD中,M、N分别是CB、CD中点,且AM⊥BC于M,AN⊥CD于N, ∠MAN=80°,则∠B+∠D的度数是
 |  |  | |||
(3) (4) (5)
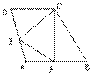
5．如图,在ΔABC中 , ∠B=2∠C,AD⊥BC于D,M为AB边中点,ME∥AC交BC于E,则AB是DE
的
倍.
6．如图,AB∥CD,E是AD中点,CF⊥AB于F。求证:CE=EF
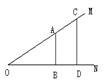7．如图,A、C是∠MON的OM边上两点,AB⊥ON于B,CD⊥ON于D,
若OA=,OB=CD,且OD+AB=1.求∠MON的度数