第6课 数的开方与二次根式
〖知识点〗
平方根、立方根、算术平方根、二次根式、二次根式性质、最简二次根式、
同类二次根式、二次根式运算、分母有理化
〖大纲要求〗
1.理解平方根、立方根、算术平方根的概念,会用根号表示数的平方根、立方根和算术平方根。会求实数的平方根、算术平方根和立方根(包括利用计算器及查表);
2.了解二次根式、最简二次根式、同类二次根式的概念,会辨别最简二次根式和同类二次根式。掌握二次根式的性质,会化简简单的二次根式,能根据指定字母的取值范围将二次根式化简;
3.掌握二次根式的运算法则,能进行二次根式的加减乘除四则运算,会进行简单的分母有理化。
内容分析
1.二次根式的有关概念
(1)二次根式
式子![]() 叫做二次根式.注意被开方数只能是正数或O.
叫做二次根式.注意被开方数只能是正数或O.
(2)最简二次根式
被开方数所含因数是整数,因式是整式,不含能开得尽方的因数或因式的二次根式,叫做最简二次根式.
(3)同类二次根式
化成最简二次根式后,被开方数相同的二次根式,叫做同类二次根式.
2.二次根式的性质 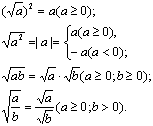
3.二次根式的运算
(1)二次根式的加减
二次根式相加减,先把各个二次根式化成最简二次根式,再把同类三次根式分别合并.
(2)三次根式的乘法
二次根式相乘,等于各个因式的被开方数的积的算术平方根,即
![]()
二次根式的和相乘,可参照多项式的乘法进行.
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,那么这两个三次根式互为有理化因式.
(3)二次根式的除法
二次根式相除,通常先写成分式的形式,然后分子、分母都乘以分母的有理化因式,把分母的根号化去(或分子、分母约分).把分母的根号化去,叫做分母有理化.
〖考查重点与常见题型〗
1.考查平方根、算术平方根、立方根的概念。有关试题在试题中出现的频率很高,习题类型多为选择题或填空题。
2.考查最简二次根式、同类二次根式概念。有关习题经常出现在选择题中。
3.考查二次根式的计算或化简求值,有关问题在中考题中出现的频率非常高,在选择题和中档解答题中出现的较多。
考查题型
1.下列命题中,假命题是( )
(A)9的算术平方根是3 (B)的平方根是±2
(C)27的立方根是±3 (D)立方根等于-1的实数是-1
2.在二次根式, , , , 中,最简二次根式个数是( )
(A) 1个 (B)2个 (C)3个 (D)4个
(2)下列各组二次根式中,同类二次根式是( )
(A),3 (B)3, (C), (D),
3. 化简并求值,+,其中a=2+,b=2-
4.+1的倒数与-的相反数的和列式为 ,计算结果为
5.(-)2的算术平方根是 ,27的立方根是 ,的算术平
方根是 ,的平方根是 .
考点训练:
1.如果x2=a,已知x求a的运算叫做 ,其中a叫做x的 ;已知a求x的运算叫做 ,其中x叫做a的 。
2.(-)2的平方根是 ,9的算术平方根是 , 是-64的立方根。
3.当a<0时,化简∣a∣++= 。
4.若=2.249,=7.114,=0.2249,则x等于( )
(A)5.062 (B)0.5062 (C)0.005062 (D)0.05062
5.设x是实数,则(2x+3)(2x-5)+16的算术平方根是( )
(A)2x-1 (B)1-2x (C)∣2x-1∣ (D)∣2x+1∣
6.x为实数,当x取何值时,下列各根式才有意义:
(1)( )(2) ( )(3)( )
(4) ( )(5) ( )(6)+( )
7.等式=成立的条件是( )
(A)-2<x≤3 (B)-2≤x≤3 (C)x>-2 (D)x≤3
8.计算及化简:
(1)(-7)2 (2) (3)
(4)(b>1) (5)(x>3y)
(6)(-6)(4+)-(2-3)2
(7)已知方程4x2-2ax+2a-3=0无实数根,
化简+|a-6|
解题指导
1.下列命题:(1)任何数的平方根都有两个(2)如果一个数有立方根,那么它一定有平方根(3)算术平方根一定是正数(4)非负数的立方根不一定是非负数,错误的个数为( )
(A)1 (B)2 (C)3 (D)4
2.已知=0.794,=1.710,=3.684,则等于( )
(A)7.94 (B)17.10 (C)36.84 (D)79.4
3.当1<x<2时,化简∣1-x∣+的结果是( )
(A)-1 (B)2x-1 (C)1 (D)3-2x
4.+()2的值一定是( )
(A)0 (B)4-2x (C)2x-4 (D)4
5.比较大小:
(1)3 (2)- 2-1 (3)- -
6.化简:(2b>a)
7.计算:(+-2)-(-)
8.已知a=,b=,求a2-5ab+b2的值。
9.计算:9÷3× 10.化简:
11.设的整数部分为a,小数部分为b,求a2+ab+b2的值。
独立训练
1.-的倒数是 ;-的绝对值是 。
2.的有理化因式是 ,的有理化因式是 。
3.与的关系是 。
4.三角形三边a=7,b=4,c=2,则周长是 。
5.直接写出答案:
(1)·÷= ,(2)= ,(3)(-2)8(+2)8= 。
6.如果-的相反数与+互为倒数,那么( )
(A)a、b中必有一个为0 (B)∣a∣=∣b∣(C)a=b+1 (D)b=a+1
7.如果+=(x-2)+(3-x),那么x的取值范围是( )
(A)x≥3 (B)x≤2 (C)x>3 (D)2≤x≤3
8.把(a-b)化成最简二次根式,正确的结果是( )
(A) (B) (C)- (D)-
9.化简-3x-+的结果必为( )
(A)正数 (B)负数 (C)零 (D)不能确定
10.计算及化简:
(1)(5··3) (2)+-4-2(+1)0
(3)(-+)÷ (4) (a>b)
11.已知=,求÷(-的值x-2)。
12.先化简,再求值:( + )+
其中x=2 - ,y=2 +
13.设的整数部分为m,小数部分为n,求代数式m+n+的值。
14.试求函数t=2-的最大值和最小值。
15.如果a+b+|-1|=4+2-4,那么a+2b-3c的值