初中毕业升学考试数学试卷4
注意事项：1.试卷分第一部分和第二部分，第一部分满分50分，第二部分满分80分，本卷满分130分.全卷共五大题,29小题.考试时间120分钟.
2.数学考试允许考生使用计算器.解答中,如果没有特别说明,结果应保留准确值.
第一部分(50分)
一、填空题（本题共8小题,每空1分，共16分.把答案填在题中横线上）
1．
=
；
=__________.
2．
的倒数是
；
的立方根是__________；4的算术平方根是__________.
3．分解因式：
=
；计算
=__________.
4．已知
，若
是
的余角，则=
度，
=__________（结果保留四个有效数字）.
5．若代数式
的值等于零，则
= ；当
时，代数式的值等于__________.
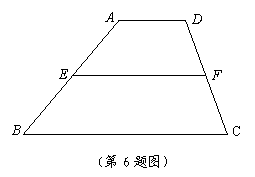
6．如图，在梯形
中，
，E、F分别是AB、CD的中点，连结EF，若
，则
=__________度，EF=_____________.
 | |||
 | |||
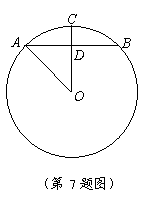
7．如图，
的半径是10cm，弦AB的长是12cm，OC是的半径且
，垂足为D，则OD=__________cm，CD=__________cm.
8．写出一个一次函数的解析式，使它的图象与x轴的夹角为
.这个一次函数的解析式是：____ _______________.
二、解答下列各题：本题共6小题，第9-13小题每题6分，第14小题4分，共34分.解答应写出文字说明，证明过程和推演步骤.
9．计算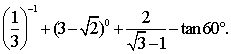
10．解不等式组：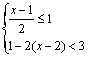
并把它的解集在数轴上表示出来.
11．请你先化简，再选取一个使原式有意义，而你又喜爱的数代入求值：
12．知一次函数
的图象与反比例函数
的图象交于点P(4，n).
（1）求n的值.（2）求一次函数的解析式.
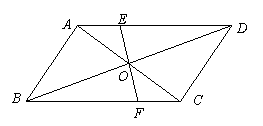
13．已知：如图，在
ABCD中，对角线AC、BD相交于点O，EF过点O分别交AD、BC于点E、F.
求证：OE=OF.
 |
14．如图，在Rt
中，
.
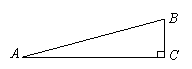（1）作AB边的垂直平分线DE交AC于点D、AB于点E，连结BD（尺规作图，不写作法，保留作图痕迹）.
（2）在（1）的基础上，若BC=1，则AD=__________，
=__________.
第二部分（80分）
三、选择题（本大题共8个小题；每小题3分，共24分，每小题都给出代号为A、B、C、D的四个结论，其中只有一个结论正确，请将正确结论的代号填在题后的括号内）
15．下列运算中，正确的是 【 】
（A）
（B）
与
是同类根式
（C）
（D）
16．满足两实数根的和等于4的方程是 【 】
（A）
（B）
（C）
（D）
17．如果
是多项式
的一个因式，则m等于 【 】
（A）6
（B）
（C）3
（D）
18．已知圆锥的侧面展开图的面积是
，母线长是10cm，则圆锥的底面圆的半径为
【 】
（A）2cm (B)6cm (C)3cm (D)4cm
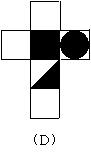
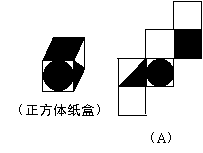
19．如图，有一个正方体纸盒，在它的三个侧面分别画有三角形、正方形和圆，现用一把剪刀沿着它的棱剪开成一个平面图形，则展开图可以是 【 】
 | |||||||
 |  | ||||||
 | |||||||
 |
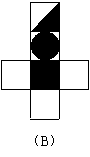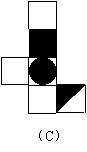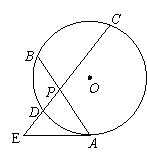20．
如图，已知的弦AB、CD相交于点P，PA=4cm，PB=3cm，PC=6cm，EA切于点A，AE与CD的延长线交于点E，若AE=
cm，则PE的长为
【 】
（A）4cm （B）3cm
（C）5cm
（D）
cm
21．已知：
，则直线
一定经过
【 】
（A）第一、二象限 （B）第二、三象限
（C）第三、四象限 （D）第一、四象限
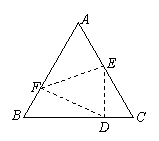22．
如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且
，则CE的长是 【 】
（A）
（B）
（C）
（D）
四、解答题：本题共4小题，第23、24小题每题6分，第25、26小题每题7分，共26分.解答应写出文字说明，证明过程和推演步骤.
23．
方程：
| 组别 | 分组 | 频数 | 频率 |
| 1 | 89.5~99.5 | 4 | 0.04 |
| 2 | 99.5~109.5 | 3 | 0.03 |
| 3 | 109.5~119.5 | 46 | 0.46 |
| 4 | 119.5~129.5 | b | c |
| 5 | 129.5~139.5 | 6 | 0.06 |
| 6 | 139.5~149.5 | 2 | 0.02 |
| 合计 | a | 1.00 | |
24． 了解初三毕业班学生一分钟跳绳次数的情况，某校抽取了一部分初三毕业生进行一分钟跳绳次数的测试，将所得数据进行处理，可得频率分布表.
频率分布表 （1）这个问题中，总体是______________________.
样本容量a=_______________.
（2）第四小组的频数b=__________，频率c=_______.
（3）若次数在110次（含110次）以上为达标，试估计该校初三毕业生一分钟跳绳次数的达标率是多少？
（4）在这次测试中，学生跳绳次数的中位数落在哪个小组内？
25．学校为了美化校园环境，在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃.
（1）若请你在这块空地上设计一个长方形花圃，使它的面积比学校计划新建的长方形花圃的面积多1平方米，请你给出你认为合适的三种不同的方案.
（2）在学校计划新建的长方形花圃周长不变的情况下，长方形花圃的面积能否增加2平方米？如果能，请求出长方形花圃的长和宽；如果不能，请说明理由.
26．一平面内，已知点O到直线l的距离为5，以点O为圆心，r为半径画圆.探究、归纳：
（1）当r=__________时，上有且只有一个点到直线l的距离等于3.
（2）当r=_________时，上有且只有三个点到直线l的距离等于3.
（3）随着r的变化，上到直线l的距离等于3的点的个数有哪些变化？并求出相对应的r的值或取值范围（不必写出计算过程）.
五、解答下列各题：本题共3小题，每小题10分，共30分.解答应写出文字说明，证明过程和推演步骤.
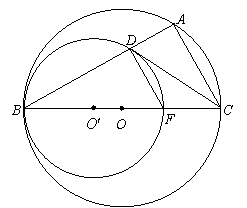
27．已知：如图，⊙O与⊙O′内切于点B，BC是⊙O的直径，BC=6，BF为⊙O′的直径，BF=4，⊙O的弦BA交⊙O′于点D，连结DF、AC、CD.
（1）求证：DF//AC.
（2）当
等于多少度时，CD与⊙O′相切？并证明你的结论.
（3）在（2）的前提下，连结FA交CD于点E，求AF、EF的长.
 |
28．阅读下列一段文字，然后解答问题.
修建润扬大桥，途经镇江某地，需搬迁一批农户，为了节约土地资源和保护环境，政府决定统一规划建房小区，并且投资一部分资金用于小区建设和补偿到政府规划小区建房的搬迁农户.建房小区除建房占地外，其余部分政府每平方米投资100元进行小区建设；搬迁农户在建房小区建房，每户占地100 平方米，政府每户补偿4万元，此项政策，吸引了搬迁农户到政府规划小区建房，这时建房占地面积占政府规划小区总面积的20%.
政府又鼓励非搬迁户到规划小区建房，每户建房占地120平方米，但每户需向政府交纳土地使用费2.8万元，这样又有20户非搬迁户申请加入.此项政策，政府不但可以收取土地使用费，同时还可以增加小区建房占地面积，从而减少小区建设的投资费用.若这20户非搬迁户到政府规划小区建房后，此时建房占地面积占政府规划规划小区总面积的40%.
（1）设到政府规划小区建房的搬迁农户为x户，政府规划小区总面积为y平方米.
可得方程组 解得
（2）在20户非搬迁户加入建房前，请测算政府共需投资 __________万元
在20户非搬迁户加入建房后，请测算政府将收取的土地使用费投入后，还需投资
__________万元.
（3）设非搬迁户申请加入建房并被政府批准的有z户，政府将收取的土地使用费投入后，还需投资p万元.①求p与z的函数关系式；②当p不高于140万元，而又使建房占地面积不超过规划小区总面积的35%时，那么政府可以批准多少户非搬迁户加入建房？
29．已知抛物线
与x轴交于两点
、
，与y轴交于点C，且AB=6.
（1）求抛物线和直线BC的解析式.
（2）在给定的直角坐标系中，画出抛物线和直线BC.
（3）若
过A、B、C三点，求的半径.
（4）抛物线上是否存在点M，过点M作
轴于点N，使
被直线BC分成面积比为
的两部分？若存在，请求出点M的坐标；若不存在，请说明理由.
 |
中考数学试题
参考答案及评分标准
一、填空题（每空1分，共16分）
1．-7,12； 2. 
； 3．
； 4. 54,0.8090；
5. 
； 6．50,6； 7. 8,2； 8. 
(b可取任意实数),如y=x（略）
二、解答题（第9-13小题，每题6分，第14小题4分，共34分）
9．原式=
……………………………4分
有理数全对给1分，无理数全对给1分
=5.………………………………………6分
10．解不等式①，得
.……………………2分
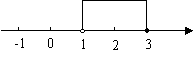解不等式②，得
……………………4分
不等式组的解集是
…………5分
这个不等式组的解集在数轴上表示如下：
…6分
11．原式=
……………………………………………… 2分
=
………………………………………………………………… 3分
.………………………………………………………………………… 4分
a可取
以外的任何一个实数，然后再求出相应的代数式的值.……………… 6分
12．（1）由题意得：
，
………………………………… 3分
（2）由点P（4，2）在上，
…………… 4分
.……………………………………………………………… 5分
一次函数的解析式为
.……………………………… 6分
13. ∵四边形ABCD是平行四边形，∴AD//BC……………………… 1分
OA=OC. ………………………………………………………… 2分
，………………………………………… 3分
，……………………………4分
…………………………5分
∴OE=OF. ……………………………6分
14. （1）作出AB边的中垂线并标出D、E，连结BD.……………2分
（2）AD=2………………………………………………………3分
…………………………………………4分
（注：填
不扣分）
三、选择题（每小题3分，共24分）
| 题号 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 答案 | B | A | D | C | C | A | B | D |
四、解答下列各题（第23、24小题每题6分，第25、26小题每题7分，共26分）
23．原方程可化为
，…………………………………1分
设
则
……………………………2分
解得 y=0或y=2.……………………………3分
当y=0时，
，即
，此方程无解.……………………4分
当y=2时，
，解得x=1. ……………………………5分
经检验x=1是原方程的根.∴原方程的根是x=1. ……………………………6分
24．（1）初三毕业班学生一分钟跳绳次数的全体.………… 1分
a=100.………………………………………………………2分
（2）b=39.…………………………………………………3分
c=0.39. ………………………………………………4分
（3）达标率为93%.………………………………………5分
（4）落在第3小组.………………………………………6分
25．（1）方案1：长为
米，宽为7米.……………………………1分
方案2：长为9米，宽为米.……………………………2分
方案3：长=宽=8米.……………………………3分
（注：本题方案有无数种，写对一个得1分，共3分.用图形示意同样给分.）
（2）在长方形花圃周长不变的情况下，长方形花圃面积不能增加2平方米.……4分
由题意得长方形长与宽的和为16米.设长方形花圃的长为x米，则宽为（16-x）米.
法一：x(16-x)=63+2， ……………5分
x2-16x+65=0，
，
∴此方程无解.
∴在周长不变的情况下，长方形花圃的面积不能增加2平方米.…………………7分
法二：S长方形=x(16-x)=-x2+16x……………………………5分
=-(x-8)2+64.
∴在长方形花圃周长不变的情况下，长方形的最大面积为64平方米，因此不能增加2平方米.……………………………………………………………7分
26．（1）r=2.……………………………1分
（2）r=8.………………………………2分
（3）当
时，上没有点到直线l的距离等于3.………………3分
（注：未写
不扣分）
当r=2时，上有且只有1个点到直线l的距离等于3.…………………4分
当
时，上有且只有2个点到直线l的距离等于3.…………5分
当r=8时，上有且只有3个点到直线l的距离等于3.…………………6分
当
时，上有且只有4个点到直线l的距离等于3.………………7分
五、答下列各题（本小题10分，共30分）
27．（1）法一：
是的直径，BF是
的直径，……1分
………………………2分
………………………………………3分
法二：过点B作两圆的外公切线MN，…………………1分
…………………………………………2分
（2）当
时，CD与相切.……………………4分
法一：连结
，∵的直径BF=4，的直径BC=6，
∴
…………………………………………5分
在
中，由BF=4，，
∴DF=2，∴
……………………6分
为直角三角形，
.
又∵点D在上，∴CD与相切.……………7分
法二：∵的直径BF为4，的直径BC为6，∴FC=2.
在
中，BF=4，，
∴DF=2，
.∴DF=FC.
………………………………5分
连结，
，…………………6分
，即
，
又∵点D在上，∴CD与相切.………………7分
（3）在
中，
在
中，
…………………………………………………………………8分
在
中，
………………9分
，
…………………………10分
28．（1）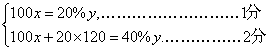
（2）192…………………………………5分
112…………………………………6分
（3）①
………………………………7分
②由题意得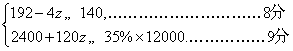
解得
∴政府可批准13、14或15户非搬迁户加入建房.………10分
29．（1）由题意得：
………………1分
解得
……………………………2分
经检验m=1，∴抛物线的解析式为：
………………3分
或：
由
得，
或
……………………1分
……………………………………2分
抛物线的解析式为………………3分
由
得
∴A（-5，0），B（1，0），C（0，-5）.
设直线BC的解析式为
则
∴直线BC的解析式为
……………………4分
(2)图象略.……………………………………………5分
（3）法一：在
中，
……………………6分
.
又
………………………………7分
∴的半径
………………………8分
法二：
由题意，圆心P在AB的中垂线上，即在抛物线
的对称轴直线
上，设P（-2，-h）（h＞0），………………………………6分
连结PB、PC，则
，
由
，即
，解得h=2.………………………7分
的半径
.………………………… 8分
法三：
延长CP交于点F.…………………………6分
为的直径，
又
……………………………7分
又
的半径为
……………………8分
（4）设MN交直线BC于点E，点M的坐标为
则点E的坐标为
若
则
解得
（不合题意舍去），
……………………9分
若
则
解得
（不合题意舍去），
存在点M，点M的坐标为
或（15，280）.……………………10分
.