初中毕业升学数学模拟试题
一、选择题（本题满分24分，共有8个小题，每小题3分）
1、下列运算正确的是（ ）
A、
B、
C、
D、
2、已知⊙O直径为10cm，弦AB的弦心距为3 cm，则弦AB的长为（ ）
A、4cm B、5cm C、8cm D、10cm
3、函数
的图象不经过第（ ）象限
A、一、三 B二、四 C、一、二 D、三、四
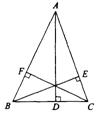
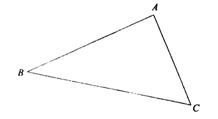
4、如图，△ABC中，AC=AB，AD、BE、CF分别为BC、AC、AB边上的高，则图中共有（ ）对全等三角形
A 、4 B、5 C、6 D、7
5、我国自1999年10月 l日起，对储蓄利息征收20％的利息税，取款由银行代扣，小明存了100元的一年定期储蓄，存满1年，取出101.8元，则一年期定期存款利息为（ ）
A、2.25% B、0.225% C、1.8% D、0.18%
6、两圆半径分别为6cm和4cm，圆心距为8 cm，则两圆的位置关系是（ ）．
A、内切 B、相交 C、外切 D、外离
7、下列说法：
（1）
的倒数是
（2）
时，
.
（3）顺次连结对角线相等的四边形各边中点，所得的四边形为正方形．
（4）关于x的方程
的两根的平方和为11，则m的值为1或–3
其中正确的是（ ）
A、（1）（2） B、（1）（4） C、（1）（2）（3）（4） D、（2）（3）
8、已知正九边形边长为a，则其外接圆半径等于（ ）．
A、
B、
C、
D、
二、填空题（本题满分24分，共有8个小题，每小题3分）
9、如果分式
的值为0，则x=_______.
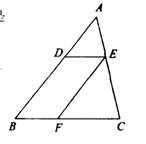
10、已知，如图DE∥BC，EF∥AB，如果AD：DB=2：3，则CF：CB=_______.
11、函数
的自变量x的取值范围是______.
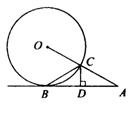
12、如图，已知AB切⊙○于B，AO交⊙○于点C，CD⊥AB且交AB于D，∠A=360，则∠BCD的度数是______.
13、分解因式：
=_______.
14、函数
中，当x=______时,y=0
15、在△ABC中，
以点C为圆心的圆与AB相切，则⊙○的半径长等于_____cm
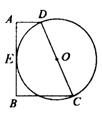
16、如图，梯形ABCD中，AD∥BC，
，以CD为直径的⊙○切AB于E，AD=3，BC=4，则⊙○直径CD的长是______.
三、作图题（本题满分4分,只有一个小题）
用圆规、直尺作图，不写作法，但要保留痕迹.
17、三条道路围成一个三角形，为搞绿化在其中建一个圆形花坛，请你在保证圆半径最大的情况之下画出此圆。
四、解答题（本题满分62分，共有9个小题）
18、（本小题满分6分）
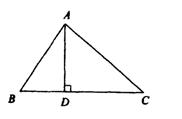已知：斜边为10的直角三角形中，两直角边为a、b且a、b为关于x的一元二次方程
的两根，求m的值.
19、（本小题满分6分）
样本数据为：1、2、1、3、3
求：（1）平均数，中位数及众数；
（2）方差．
20、（本小题满分6分）
在△ABC中，已知
，AD⊥BC于D，AD=3，AC=5．
求：AB和BC的长．
21、化简下列各式（本小题满分6分）
（1）
（2）
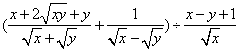
22、（本小题满分6分）
甲乙两村要合作完成绿化某茶座荒山的任务，如果先由甲村完成总任务的一半，乙村再完成另一半，那么乙村要比甲村少用3天，实际情况是甲村工作了3天后，为了不耽误农时，乙村也来合作，结果两村又合作了12天就全面完成任务，求甲、乙两村单独完成全部绿化任务各需几天？
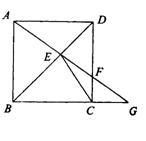23、（本小题满分6分）
已知正方形ABCD中，E是BD上一点，延长AE交CD于F，交BC延长线与G.
求证：（1）ADE≌△CDE；
（2）
24、（本小题满分6分）
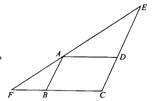已知：如图，四边形ABCD是平行四边形，且∠EAD=∠BAF.
（1）求证：△CEF是等腰三角形；
（2）△CEF的哪两边之和恰好等于平行四边ABCD的周长？写出你的结论.
25、（本小题满分8分）
甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每副定价20元，乒乓球每盒定价5元，现两家商店搞促销活动，甲店：每买一副球拍赠一盒乒乓球；乙店：按定价的9折优惠。某班级需购球拍4副，乒乓球若干盒（不少于4盒）．
（1）设购买乒乓球盒数
（盒），在甲店购买的付款数为
（元），在乙店购买的付款数为
（元），分别写出在两家商店购买的付款数与乒乓球盒数之间的函数关系式.
（2）就乒乓球盒数讨论去哪家商店购买合算？
26、（本小题满分8分）
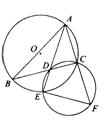
已知：△ABC中，∠BAC的平分线交BC于D，交外接圆⊙O于E，延长AC交过点C、D、E的圆于F.
（1）求证：
（2）若AE=6，EF=3求：AF
AC的值.
27、（本小题满分10分）
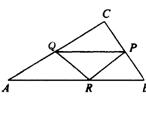已知，在Rt△ABC中，
，BC、CA、AB的边长分别为a，b，c，并在其上分别取点P、Q、R，使CQ＝2BP，AR＝3BP，BP＝x，连结P、Q、R三点，设△PQR的面积为S．不等式
的解与关于x的不等式
的解相同，b为
与
有一次公因式的b的正数解.
（1）求a、b的值；
（2）求S关于自变量x的解析式；
（3）x取什么值时，S有最小值，最小值是多少？（精确到0.l）