初中毕业升学数学模拟试题九
一、选择题（本题满分24分，共有8个小题，每个小题3分）
1、下列等式成立的是（ ）
A、
B、
C、
D、
2、两圆直径分别为6和8，圆心距为7，这两个圆的公切线最多有（ ）条
A、1 B、2 C、3 D、4
3、已知，直线
与x轴交点在x轴的正半轴上，有下列结论：
A、
B、
C、
D、 
其中正确的有（ ）个.
A、1 B、2 C、3 D、4
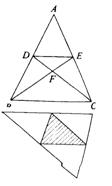
4、已知：如右上图，D、E分别是AB、AC上的点，DC、EB交于F，若AB=AC–AD=AE，则图中共有（ ）对全等三角形．
A、2 B、3 C、4 D、5
5、某住房小区有一块三角形空地（如右下图），如果把各边中点连线所围成的三角形区域种花，其余铺成绿地，那么种花区域与绿地的面积比是（ ）
A、
B、
C、
D、
6、已知
是方程
的两个根，则
的值是（ ）
A、1 B、–1 C、
D、0
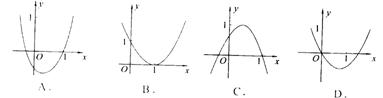
7、已知二次函数
，如果
，且a+b+c=0，则它的图象可能是（ ）
8、同圆的外切正方形和内接正方形的相似比是（ ）
A、1：2 B、2：1
C、
D、
二、填空题（本题满分24分，共有8个小题，每小题3分）
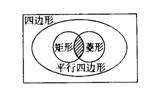
9、图中，阴影部分表示的四边形是______.
10、两条对角线_____的四边形是正方形.
11、函数
中，自变量x的取值范围是______.
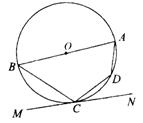12、如图⊙○的内接四边形ABCD中，AB为⊙○的直径，MN切⊙O于C，∠ADC=
，则∠BC M=_____度.
13、关于x的方程
有增根，那么增根为______.
14、要铺设一条650m长的地厂管道，由甲乙两个工程队从两头相向施工，甲队每天铺设48m，乙队每天比甲队多铺22m，乙队比甲队晚开工1天，问乙队开工多少天后，两队完成整个铺设任务的80％？
列方程解应用题，若设乙队开工x天后，两队完成整个铺设任务的80％，则根据题意可列方程应为______
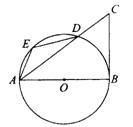
15、已知，如图AB是⊙○直径，CB是⊙○切线，AC交⊙○于D，E是
上一点，且∠EAD=∠DAB。已知BC=6，AB=8.则DE=_______.
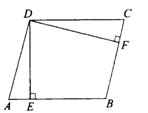16、已知：如图
ABCD中，DE⊥AB于E，DF⊥BC于F，ABCD的周长为110
，面积为
，AB：BC=6：5，sin∠EDF=_______.
三、作图题《本题满分4分）
用圆规、直尺作图，不写作法,但要保留作图痕迹.
17、改革开放以来，两个村庄走向致富路，水果产品连年丰收，他们想建一个现代化的食品加工厂，使它离两个村庄及两条铁路线的距离
都相等，请你在下图中标出它的位置.
四、解答题（本题满分62分，共有9个小题）
18、（小题满分6分）
已知：
是关于x的方程
的两个实根，且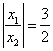
，求m值。
19、（小题满分6分）
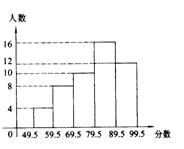
对某班学生一次数学测验成绩进行统计分析，各分数段的人数如图所示（分数取上整数），请观察图形，并回答下列问题；
（1）该班有多少名学生.
（2）89.5～99.5这一组的频数、频率分别是多少？
（3）估罚该班这次测验的平均成绩。
20、（本小题满分6分）
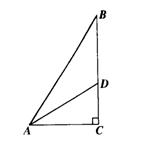已知：△ABC中，∠C=
，D是BC上一点，cotB=2，tan∠ADC=
，BD=5.
求：AD的长。
21、化简下列各式（本小题满分6分）
（1）
（2）
22、（本小题满分6分）
一个工人要完成1000个零件，起初机器出现故障，每分钟比原计划少加上4个零件，加工320个零件后，换了一台新式机器，每分钟比原计划多加工8个零件，已知用新机器加工零件的时间比前面用旧机器加工零件的时间少6分钟，求原汁划每分钟加工多少零件？
23、（本小题满分6分）
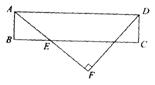
已知：如图，矩形ABCD中，AB=5，AD=20，E是BC边上的一点，BE：EC=1：2，DF⊥AF．
求：DF的长
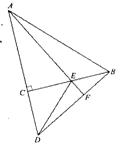
24、（本小题满分6分）
如图△ACB、△ECD都是等腰直角三角形，且C在AD上。AE的延长线与BD交于F，请你在图中找出一对全等三角形，并写出证明它们全等的过程.
25、（本小题满分8分）
某家电集团公司生产某种型号的新家电，前期投资200万元，每生产1台这种新家电，后期还需其他投资0.3万元，已知每台新家电可实现产值0. 5万元.
（1）分别求总投资额
（万元）和总利润
（万元）关于新家电的总产量
（台）的函数关系式；
（2）当新家电的总产量为900台时，该公司的盈亏不情况如何？
（3）请你利用第（l）小题中与的函数关系式，分析该公司的盈亏情况。
（注：总投资=前期投资+后期其他投资，总利润=总产值–总投资）
26、（本小题满分8分）
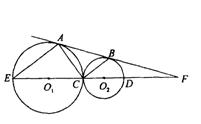
已知：⊙
和⊙
外切于点C，外公切线AB切⊙于A，切⊙于B，CE是⊙的直径，延长EC交⊙于D，交AB的延长线于F.
求证：（1）AE∥BC； （2）
（3）
27、（本小题满分10分）
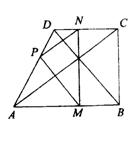如图，梯形ABCD中，AB∥CD，P、M、N分别是AD、AB、CD上的点，且PM∥BD，PN∥AC.
（l）求证：
（2）若AC⊥BD，AC=BD=12，并设PN=，△PMN的面积为
，求与的函数关系式；
（3）在（2）中，当x取什么数值时，△PMN的面积最大？并指出此时点P在线段AD上的位置。.