初中毕业升学统一考试数学试题
| 题号 | A卷 | B卷 | 总分 | |||||||
| 一 | 二 | 三 | 四 | 五 | 一 | 二 | 三 | 四 | ||
| 分数 | ||||||||||
(本试卷共8页,A卷16题,B卷12题,请考生准备好计算器、圆规、直尺等工具)
A卷(满分100分)
一、选择题(本大题共5小题,每小题4分,共计20分)
说明:将各题唯一正确的答案代号填到题后的括号内。
1、一元二次方程![]() 的解是 ( )
的解是 ( )
A、x
= 2 B、x =-2 C、x1
= 2 ,x2 = -2 D、x1=
![]() ,x2 =
,x2 = ![]()
2、一元二次方程![]() 的根的情况是( )
的根的情况是( )
(A)有两个不相等的实数根 (B)有两个相等的实数根
(C)没有实数根 (D)不能确定
3、在Rt△ABC中,∠C=90°,AC=4,BC=3,则cosB的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知⊙O1和⊙O2的半径分别为2和5,O1O2=7,则⊙O1和⊙O2的位置关系是( )
A、外切 B、内切 C、相交 D、相离
5、抛物线![]() 的对称轴是(
)
的对称轴是(
)
A、直线x=-3 B、直线x=3![]()
C、直线x=-2 D、直线x=2
二、填空题(本大题共5小题,每小题4分,共计20分。说明:将各题结果填在题后的横线上。)
6、请写出一个在第二象限的点的坐标_______________;
7、某班30名女生身高检测结果如下表(单位:米)
| 身高 | 1.57 | 1.58 | 1.59 | 1.60 | 1.61 | 1.62 | 1.64 | 1.65 |
| 人数 | 2 | 2 | 3 | 3 | 8 | 7 | 3 | 2 |
 则该班女生身高的众数是________米;
则该班女生身高的众数是________米;
8、正六边形内接于⊙O,⊙O的半径为5㎝,则这个正六边形
的边长为______㎝;
9、如图,四边形ABCD内接于⊙O,∠BOD=160°,则∠BAD的度数是_________,
∠BCD的度数是_______;
10、已知矩形ABCD的一边AB=2㎝,另一边AD=4㎝,则以直线AD为轴旋转一周所得到的图形是_______,其侧面积是_______________㎝2;
三、解答题(本大题共2小题,每小题10分,共计20分)
11、如图,在离地面高度6米的C处引拉线固定电线杆,拉线和地面成61°角,求拉线AC的长以及拉线下端点A与杆底D的距离AD。(精确到0.01米)

12、如图,在△ABC中,以BC为直径的⊙O交AB于D,交AC于E,BD=CE。
求证:AB=AC

四、解答题(本大题共4小题,其中第13题8分,14题、15题各10分,16题12分,共计40分)
13、解方程组。![]()
14、某专业户要出售100只羊,现在市场上羊的价格为每千克11元,为了估计这100只羊能卖多少钱,该专业户从中随机抽取5只羊,每只羊的重量如下(单位:千克)
26 31 32 36 37
⑴估计这100只羊每只羊的平均重量;
⑵估计这100只羊能卖多少钱。
15、某地区现在有果树12000棵,计划今后每年栽果树2000棵。
⑴求果树总数y(棵)与年数x(年)的函数关系式;
⑵预计到第5年该地区有多少棵果树?
16、某工厂贮存240吨煤,由于改进炉灶木结构和烧煤技术,每天能节约2吨煤,使贮存的煤比原计划多用4天。问原计划每天烧煤多少吨?
B卷(满分100分)
一、填空(本大题共5小题,其中1、2、3、4题各3分,第5题4分,共计16分
说明:将各题结果填在横线上
1、某房屋开发公司经过几年的不懈努力,开发建设住宅面积由2000年4万平方米,到2002年的7万平方米。设这两年该房屋开发公司开发建设住宅面积的年平均增长率为x ,则可列方程为______________;
2、借助计算器可以求得![]()
![]() ……,仔细观察上面几道题的计算结果,试猜想
……,仔细观察上面几道题的计算结果,试猜想![]() _______________;
_______________;
 3、试写出一个开口方向向上,对称轴为直线x = 2,且与y轴的交点坐标为(0,3)的抛物线的解析式 __________________________________;
3、试写出一个开口方向向上,对称轴为直线x = 2,且与y轴的交点坐标为(0,3)的抛物线的解析式 __________________________________;
4、如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B,C是弧AB上任意一点,
过C作⊙O的切线分别交PA、PB于D、E,若△PDE的周长为12,
则PA长为______________;
5、已知二次函数![]() 的图象与x轴交于点A、B两点,在x轴上方的
的图象与x轴交于点A、B两点,在x轴上方的
抛物线上有一点C,且△ABC的面积等于10,则C点的坐标为_________________;
二、解答题(本大题共3小题,其中第题8分,第7题10分,第8题12分,共计30分)
6、已知方程组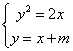 有两个实数解
有两个实数解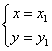 和
和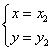 ,且
,且![]() ,求m的值
,求m的值
7、如图,PA是⊙O的切线,切点为A,PCB是⊙O的割线,交⊙O于C、B两点,半径OD⊥BC,垂足为E,AD交PB于点F,BF=PF。
⑴求证:PA=PF
⑵若CF=1,求切线PA的长。

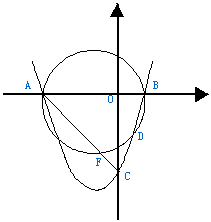
8、如图,抛物线![]() 与x轴交于A、B两点,与y轴 交于点C,D是抛物线上一点,其坐标为(
与x轴交于A、B两点,与y轴 交于点C,D是抛物线上一点,其坐标为(![]() ),B点坐标为(1,0)。
),B点坐标为(1,0)。
⑴求抛物线的解析式;
⑵经过A、B、D三点的圆交AC于F,交直线y = x + 3于点E。试判断△ABC的形状,并加以证明。
三、解答题(本大题共3小题,每小题14分,共计42分)
9、某水产品养殖加工厂有200名工人,每名工人每天平均捕捞水产品50千克,或将当日所捕捞的水产品40千克进行精加工。已知每千克水产品直接出售可获利润6元,精加工后再出售,可获利润18元。设每天安排x名工人进行水产品精加工
⑴求每天做水产品精加工所得利润y(元)与x的函数关系式;
⑵如果每天精加工的水产品和未来得及加工的水产品全部出售,那么如何安排生产可使一天所获利润最大?最大利润是多少?
10、阅读下列材料:“父亲和儿子同时出去晨练。如图,实线表示父亲离家的路程y(米)与时间x(分钟)的函数图象;虚线表示儿子离家的路程y(米)与时间x(分钟)的图象。由图象可知,他们在出发10分钟时经一次,此时离家400米;晨练了30分钟,他们同时到家。”
根据阅读材料给你的启示,利用指定的直角坐标系(如图)或用其他方法解答问题:
一巡逻艇和一货轮同时从A港口前往相距100千米的B港口,巡逻艇和货轮的速度分别为100千米/时和20千米/时,巡逻艇不停的往返于A、B两港口巡逻(巡逻艇调头的时间忽略不计)。
⑴货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次?
⑴出发多少时间巡逻艇与货轮第三次相遇?此时离A港口多少千米?


10、已知:如图1,给出下列6个论断,①AB是⊙O1的直径;②EC是⊙O1的切线;
③AC是⊙O2的直径;④BC·EC=DE·BD;⑤DE∥BC;⑥DE·BC=2CE2。
⑴将6个论断中的3个作为题设,2个论断作为结论,写出一个真命题,并加以证明;
⑵如果AB不是⊙O2直径(如图2),你能否再从其余5 个论断中选取一个论断作为题设,一个论断作为结论,使其成为真命题(不要求证明)。若能,请写出两个;若不能,请你再添加一个条件,写出两个真命题。

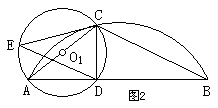
四、解答题(本大题共1小题,共12分)
问题:要将一块直径为2m的半圆形铁皮加工成一个圆柱的两个底面和一个圆锥的底面。
操作:
方案一:在图1中,设计一个圆锥底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图);
方案二:在图2中,设计一个圆柱两个底面最大,半圆形铁皮得以最充分利用的方案(要求:画示意图)。
探究:
⑴求方案一中圆锥底面的半径;
⑵求方案二中半圆圆心为O,圆柱两个底面圆心为O1、O2,圆锥底面的圆心为O3,试判断以
O1、O2、O3、O为顶点的四边形是什么样的特殊四边形,并加以证明。


(说明:本套试题A卷为毕业卷,共100分;升学为A卷×50% + B卷,共150分)