初中毕业生升学文化数学考试
第Ⅰ卷（选择题 共30分）
一、选择题（每小题2分，共30分）：
1．下列四个数中，在－2到0之间的数是（ ）．
(A) －1 (B) 1 (C) －3 (D) 3
２．计算x 6÷x 3的结果是（ ）．
(A) x 9 (B) x 3 (C) x 2 (D) 2
3．光年是天文学中的距离单位，1光年大约是9 500 000 000 000km，用科学记数法可表示为( )．
(A) 950×1010 km (B) 95×1011 km (C) 9.5×1012 km (D) 0.95×1013 km
4．在1，－1，－2这三个数中，任意两数之和的最大值是（ ）．
(A) 1 (B) 0 (C) －1 (D) －3
5．下列二次根式中，最简二次根式是( )．
(A)
(B)
(C) 
(D) 
6．方程x2 －4x＋4＝0根的情况是（ ）．
(A)有两个不相等的实数根 (B) 有两个相等的实数根
(C) 有一个实数根 (D)没有实数根
7. 不等式x－2＜0的正整数解是( ).
(A)1 (B)0，1 (C)1，2 (D)0，1，2
8．在平面直角坐标系中，点P（2，1）关于原点对称的点在（ ）．
(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
9．抛物线y＝(x－2)2的顶点坐标是（ ）．
(A)（2，0） (B)（－2，0） (C)（0，2） (D)（0，－2）
10. 如果∠α＝20°，那么∠α的补角等于（ ）．
(A) 20° (B) 70° (C) 110° (D) 160°
11．在比例尺是1∶8000的南京市城区地图上，太平南路的长度约为25 cm，它的实际长度约为（ ）．
(A) 320 cm (B) 320 m (C) 2000 cm (D) 2000 m
12．用两个边长为a的等边三角形纸片拼成的四边形是（ ）．
(A) 等腰梯形 (B) 正方形 (C) 矩形 (D) 菱形
13．在△ABC中，∠C＝90°，如果AB＝2，BC＝1，那么sinA的值是( ).
(A)
(B) 
(C)
(D)
14．如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B＝70°，则∠BAC等于（ ）．
(A) 70°
(B) 35°
(C) 20°
(D) 10°
15．如图，边长为12 m的正方形池塘的周围是草地，池塘边A、B、C、D处各有一棵树，且AB＝BC＝CD＝3 m．现用长4 m的绳子将一头羊栓在其中的一棵数上，为了使羊在草地上活动区域的面积最大，应将绳子栓在（ ）．
(A) A处 (B) B处 (C) C处 (D) D处
 |
 |
二、填空题（每小题2分，共10分）
16．计算：
＝ ．
17．分解因式：3x2－3＝ ．
18．写出一个无理数，使它与
的积是有理数： ．
19．如图，割线PAB与⊙O交于点A、B，割线PCD与⊙O交于点C、D，PA＝PC，PB＝３cm，则PD＝ cm．
20. 如图，矩形ABCD与⊙O交于点A、B、F、E，DE＝1 cm，EF＝３cm，则AB＝ cm．
|
三、（每小题５分，共25分）
21．计算：
．
22．解不等式组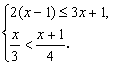
23．已知方程x
＋kx－6＝０的一个根是2，求它的另一个根及k的值．
24．已知：如图，E、F是
ABCD的对角线上的两点，AE＝CF．
求证：(1) △ABE≌△CDF；
(2) BE∥DF是平行四边形．
25．为了了解某小区居民的用水情况，随机抽查了该小区10户家庭的月用水量，结果如下：
| 月用水量（吨） | 10 | 13 | 14 | 17 | 18 |
| 户数 | 2 | 2 | 3 | 2 | 1 |
(1) 计算这家庭的平均月用水量；
(2) 如果该小区有500户家庭，根据上面的计算结果，估计该小区居民每月共用水多少吨？
四、（每小题6分，共12分）
26．在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S（m2）的反比例函数，其图象如图所示．
(1) 求p与S之间的函数关系式；
(2) 求当S＝0.5 m2时物体承受的压强p．
27．(1)如果二次函数y＝x2－2 x＋c的图象经过点（1，2），求这个二次函数的解析式，并写出该函数图象的对称轴；
(2)图象的对称轴是y轴的二次函数有无数个．试写出两个不同的二次函数解析式，使这两个函数图象的对称轴是y轴．
五、（每小题6分，共12分）
28．如图，天空中有一个静止的广告气球C，从地面A点测得C点的仰角为45°，从地面B点测得C点的仰角为60°．已知AB＝20 m，点C和直线AB在同一铅垂平面上，求气球离地面的高度（结果保留根号）．
29．某地举办乒乓球比赛的费用y（元）包括两部分：一部分是租用比赛场地等固定不变的费用b，另一部分与参加比赛的人数x（人）成正比例． 当x＝20时，y＝1600，当x＝30时，y＝2000．
(1)求y与x之间的函数关系式；
(2)如果有50名运动员参加比赛，且全部费用由运动员分摊，那么每名运动员需要支付多少元？
六、（本题7分）
30． 如果两个三角形不仅是相似三角形，而且每对对应点所在的直线都经过同一个点，那么这两个三角形叫做位似三角形，它们的相似比又称为位似比，这个点叫做位似中心．利用三角形的位似可以将一个三角形缩小或放大．
(1)选择：如图1，点O是等边三角形PQR的中心，P′、Q′、R′分别是OP、OQ、OR的中点，则△P′Q′R′与△PQR是位似三角形．此时，△P′Q′R′与△PQR的位似比、位似中心分别为（ ）．
A．2、点P B．、点P
C．2、点O D．、点O
图１ 图２
(2) 如图２，用下面的方法可以画△AOB的内接等边三角形．阅读后证明相应问题．
画法：①在△AOB内画等边三角形CDE，使点C在OA上，点D在OB上；
②连结OE并延长，交AB于点E′，过点E′作E′C′∥EC，交OA于点C′，
作E′D′∥ED，交OB于点D′；
③连结C′D′．则△C′D′E′是△AOB的内接三角形．
求证：△C′D′E′是等边三角形．
七、（本题7分）
31．某商店以2400元购进某种盒装茶叶，第一个月每盒按进价增加20%作为售价，售出50盒，第二个月每盒以低于进价5元作为售价，售完余下的茶叶．在整个买卖过程中盈利350元，求每盒茶叶的进价．
八、（本题9分）
32．如图1，在矩形ABCD中，AB＝20 cm，BC＝4 cm，点P从A开始沿折线A—B—C—D以4 cm / s的速度移动，点Q从C开始沿CD边以1 cm / s的速度移动，如果点P、Q分别从A、C同时出发，当其中一点到达D时，另一点也随之停止运动．设运动时间为t（s）．
(1) t为何值时，四边形APQD为矩形？
(2) 如图2，如果⊙P和⊙Q的半径都是2 cm，那么t为何值时，⊙P和⊙Q外切？
 | |||
 | |||
图１ 图２
九、（本题８分）
33．如图，AB⊥BC，DC⊥BC，垂足分别为B、C．
(1)当AB＝4，DC＝1，BC＝4时，在线段BC上是否存在点P，使AP⊥PD？如果存在求线段BP的长；如果不存在，请说明理由．
(2)设AB＝a，DC＝b，AD＝c，那么当a、b、c之间满足什么关系时，在直线BC上存在点P，使AP⊥PD？
