第37讲 圆柱圆锥圆台侧面积计算
一．考纲要求
会计算圆柱、圆锥、圆台的侧面积和表面积．
二．基础回顾
1．用一张边长为3лcm和4лcm的矩形卷成一个圆柱，则这个圆柱的母线长是________.
2．若圆柱的母线长为10cm，侧面积为60cm2，则圆柱的底面半径为( )．
(A)3cm (B)6cm (C)9cm (D)12cm
3．圆锥的母线与底面直径都等于8cm，则圆锥的侧面积是_______.
4．已知圆锥底面半径为r，若它的侧面积是底面积的1，5倍，则母线长_______.，展开后扇形的圆心角=_______.
5．巳知圆台的轴截面梯形的腰与下底的夹角为60°，高线长为4，中位线长为5，则圆台的侧面积是_______
三．典型例题
例1．若矩形ABCD的邻边不等，分别以直线AB、BC为轴旋转一周得两个圆柱，观察这两个圆柱的底面和侧面，则有 ( )．
(A)S底S侧都相等． (B)S底不等，S侧相等．
(C) S底相等，S侧不等．(n) S底S侧都不等．
例2．如果圆台的上底面半径为5，下底面半径为R，中截面把圆台分为上、下两个圆台，它们的侧面积的比为1：2，那么R=( )
(A)10 (B)15 (C)20 (D)25
例3．用一块圆心角为150°，面积为240лcm2的扇形硬纸片围成一个圆锥模型(相交粘贴部分忽略不计)，求圆锥模型的底面半径．
例4．巳知圆锥的轴截面周长为10cm，设腰长为x，圆锥的表面积为S，
(1) 求S关于X的函数表达式和自变量X的取值范围；
(2)画出这个函数图象，确定S的取值范围．
例5．如图，已知直角梯形ABCD，BC∥AD，∠B=90°，AB=5 cm ，BC=16cm，AD=4cm。(1)求以AB所在直线为轴旋转一周所得几何体的表面积；
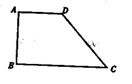(2)求以直线BC为轴旋转一周所得几何体的表面积．
四．反馈练习
1．用一张边长为20cm的正方形纸片围成一个圆柱的侧面，则这个圆柱的底面直径是( )．
(A) cm （B） cm （C）cm （D） cm
2．一个圆锥的侧面积是底面积的2倍，则这个圆锥的侧面展开扇形的圆心角为_______.
3．圆台的侧面展开图扇环圆心角为180，则圆台下底半径与上底半径之差与母线的比为( )．
(A) (B) (c) (D)不能确定
4．以AB为斜边的直角三角形ABC中，AC=5，BC=12，分别以AC、CB、BA所在直线为轴旋转而得几何体的表面积分别记作SAC、SBC、SAB，则下列不等式成立的是( )
(A) SAB> SBC> SAC (B) SBC > SAC> SAB
(C) SAC> SBC > SAB (D) SAB >SAC> SBC
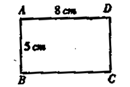5．如图，矩形的边AB=5cm，AD=8cm，分别以直线AB、AD为轴旋转一周得两个不同的圆柱，问哪个圆柱的表面积大?
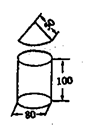
6．一车间要用铁皮加工一批元件．元件由两部分组成，一个圆柱形的铁管，上面有一个圆锥形帽子，尺寸如图所示(单位：rnm)，问总共需要多少千方厘米的铁皮(精确到个位)．
五．巩固提高
1．圆柱的底面半径为2crn，高为3crn，则它的侧面积是 crn2
2．巳知圆柱的母线长是5cm，侧面展开图的面积为20лcm2，则这个圆柱的底面半径为 cm．
3．底面半径为3cm，母线长为5cm的圆锥侧面展开图面积为 cm2
4．巳知圆锥的底面直径为80crn，母线长为90crn，则它的侧面展开图的圆心角是 ．
5．若一圆锥形烟囱帽的侧面积是2000лcm2，母线长为50cm，则这个烟囱帽的底面直径为( )．
(A)80cm (B)lOOcrn(C)40crn (D)60crn
6．圆柱铁桶的侧面展开图是边长为12лcm的正方形，则该铁桶的底面直径是( )．
(A) 12лcrn(B)6лcrn (C)12cm (D)6cm
7．两个圆锥的母线长相等．侧面积之比为1：2，底面积之比为 ( )
(A)2：1 (B)1：2 (C)1：3 (D)1：4
8．将一块半径为Rcm，圆心角为θ°的扇形铁皮做成一个圆锥形的烟囱帽，则这个圆锥的底面半径是 cm．
9．巳知圆锥的高线和底面直径相等，求底面积和侧面积之比．
10．巳知圆台形铅桶口直径为28cm，桶底直径20cm，高线长36cm；若做这样无盖铅桶100个，共需铅皮多少m2(接头损耗不计，x取3．14，= 9．06，结果保留两个有效数字)
11．若干毫升水倒人底面半径为2cm的圆柱形器皿中，量得水面的高度为6cm，若将这些水倒人轴截面是正三角形的倒圆锥形器皿中，求水面的高度．(圆锥形器皿容积V=πr2h)
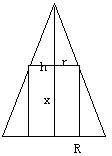
12.已知一个圆锥的底面半径为R，高为h。在其中有一个高为x的内接圆柱。
（1）求圆柱的侧面积;
（2）x为何值时，圆柱的侧面积最大？
