初中升学考试数学试卷
数 学
注意事项:
1. 本试卷共8页,总分120分,考试时间120分钟.
2. 考生答题前务必将自己所在的县、市、区、学校及姓名、准考证号填写在密封线内的相应空格处.
一、选择题(本大题10小题;每小题3分,共30分)
每小题只有一个正确答案,将你选出的答案代号填入下表相应的位置.
1. 计算a5·a5的结果是 ( )
A、a10 B、a25 C、2a5 D、2a10
2. 给出下列四个算式:①-(-1)=1;②(-1)-1=1;③(-1)0=1;④![]() .其中正确的算式有 ( )
.其中正确的算式有 ( )
A、1个 B、2个 C、3个 D、4个
3. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块大小形状完全一样的玻璃,那么最省事的办法是( )
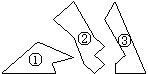
A、带①和②去 B、带①去 C、带②去 D、带③去
4. 如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于( )
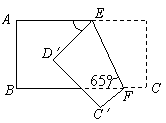
A、50° B、55° C、60° D、65°
5. 如图,面积为30m2的正方形的四个角是面积为2m2的小正方形,用计算器求得a的长为 ( )(保留3个有效数字)
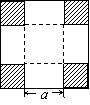
A、2.70m B、2.66m C、2.65m D、2.60m
6. 用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,其中两块木板的边数都是8,则第三块木板的边数应是 ( )
A、4 B、5 C、6 D、8
7. 如图,⊙O1与⊙O2相交于A、B两点,AC是⊙O2的切线,AD是⊙O1的切线,若BC=4,BD=9,则AB的长为
5.
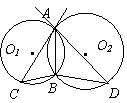
A、5 B、6 C、7 D、8
8. 现用甲、乙两种运输车将46吨抗旱物资运往灾区,甲种运输车载重5吨,乙种运输车载重4吨,安排车辆不超过10辆,则甲种运输车至少应安排
A、4辆 B、5辆 C、6辆 D、7辆
9. 如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x(件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买乙家的1件售价约为3元,其中正确的说法是 ( )
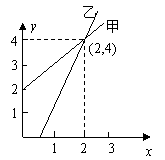
A、①② B、②③④ C、②③ D、①②③
10. 计算机利用的是二进制数,它共有两个数码0、1,将一个十进制数转化为二进制数,只需把该数写成若干个2n数的和,依次写出1或0即可,如19(十)=16+2+1=1×24+0×23+0×22+1×21+1×20=10011(二)为二进制下的5位数,则十进制数2004是二进制下的
A、10位数 B、11位数 C、12位数 D、13位数
二、填空题(本大题5小题;每小题4分,共20分).
请将答案直接填写在题后的横线上
11. 若![]() 的值等于1,且x<0,则x=_______.
的值等于1,且x<0,则x=_______.
12. 一个函数具有下列性质:①它的图象不经过第三象限;②图象经过点(-1,1);③当x>-1时函数值y随自变量x增大而增大.试写出一个满足上述三条性质的函数的解析
式______________.
13. 如图,一桥拱呈抛物线状,桥的最大高度是16米,跨度是40米,在线段AB上离中心M处5米的地方,桥的高度是_____m (π取3.14).
14. 如图,AC⊥AB,BE⊥AB,AB=10,AC=2.用一块三角尺进行如下操作:将直角顶点P在线段AB上滑动,一直角边始终经过点C,另一直角边与BE相交于点D,若BD=8,则AP的长为________.
15.某些植物发芽有这样一种规律:当年所发新芽第二年不发芽,老芽在以后每年都发芽.发芽规律见下表(设第一年前的新芽数为a)
| 第×年 | 1 | 2 | 3 | 4 | 5 | … |
| 老芽率 | a | a | 2 a | 3 a | 5 a | … |
| 新芽率 | 0 | a | a | 2 a | 3 a | … |
| 总芽率 | a | 2 a | 3 a | 5 a | 8 a | … |
照这样下去,第8年老芽数与总芽数的比值为_______(精确到0.001)
三、解答题(本大题8小题;共70分)
16. (本小题满分6分)
化简并求值:![]() ,其中
,其中![]() .
.
17. (本小题满分6分)
已知双曲线![]() 和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且
和直线y=kx+2相交于点A(x1,y1)和点B(x2,y2),且![]() 求k的值.
求k的值.
18. (本小题满分8分)
某同学进行社会调查,随机抽查了某个地区的20个家庭的收入情况,并绘制了统计图.请你根据统计图给出的信息回答:
⑴填写完成下表:
| 年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 家庭户数 |
这20个家庭的年平均收入为______万元;
⑵样本中的中位数是______万元,众数是______万元;
⑶在平均数、中位数两数中,______更能反映这个地区家庭的年收入水平.
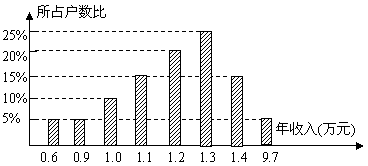

19.(本小题满分8分)
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的证明方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连结CC′,设AB=a,BC=b,AC=c,,请利用四边形BCC′D′的面积证明勾股定理:a2+b2=c2.
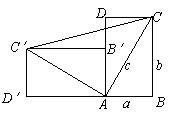

20.(本小题满分10分)
将一副三角尺如下图摆放在一起,连结![]() ,试求
,试求![]() 的余切值.
的余切值.

21. (本小题满分10分)
为了改善城乡人民生产、生活环境,我市投入大量资金,治理竹皮河污染,在城郊建立了一个综合性污水处理厂,设库池中存有待处理的污水![]() 吨,又从城区流入库池的污水按每小时
吨,又从城区流入库池的污水按每小时![]() 吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?
吨的固定流量增加.如果同时开动2台机组需30小时处理完污水,同时开动4台机组需10小时处理完污水.若要求5小时内将污水处理完毕,那么至少要同时开动多少台机组?
22. (本小题满分10分)
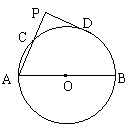
如图,AB是⊙O的直径,AC是弦,D是![]() 的中点,过点D作AC的延长线的垂线DP,垂足为P.若PD=12,PC=8,求⊙O的半径R的长.
的中点,过点D作AC的延长线的垂线DP,垂足为P.若PD=12,PC=8,求⊙O的半径R的长.

23. (本小题满分12 分)
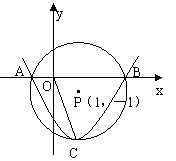
如图,在直角坐标系中,以点P(1,-1)为圆心,2为半径作圆,交x轴于A、B两点,抛物线![]() 过点A、B,且顶点C在⊙P上.
过点A、B,且顶点C在⊙P上.
⑴ 求⊙P上劣弧![]() 的长;
的长;
⑵ 求抛物线的解析式;
⑶ 在抛物线上是否存在一点D,使线段OC与PD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.

初中升学考试试卷
数学参考答案
一、选择题(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | B | D | A | C | A | B | C | D | B |
二、填空题(每小题4分,共20分)
11.![]() ;12.
;12.![]() 等(写一个即可);
等(写一个即可);
13.15; 14.2或8.(答对一个给2分); 15.0.618
三、解答题(共70分)
16.解:∵a+1=![]() +1=
+1=![]() =-
=-![]() <0……………………3分
<0……………………3分
∴原式=a+1-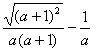 =
=![]() =a+1=-
=a+1=-![]() …… 6分
…… 6分
17.解:由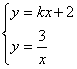 得
得![]()
∴![]() =-
=-![]() ,
,![]() =-
=-![]() ………………………………………2分
………………………………………2分
故![]() =(
=(![]() )2-2
)2-2![]() =
=![]() =10
=10
∴5k2-3k-2=0. ∴k1=1或k2=-![]() .…………………………… 4分
.…………………………… 4分
又△=4+12k>0即k>-![]() ,舍去k2=-
,舍去k2=-![]() ,故所求k值为1.……6分
,故所求k值为1.……6分
18.(1)
| 年收入(万元) | 0.6 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 9.7 |
| 家庭户数 | 1 | 1 | 2 | 3 | 4 | 5 | 3 | 1 |
(每对4个给1分)………………………………………… 2分
年平均数收入为1.6万元;……………………………… 4分
(2)中位数是1.2万元,众数是1.3万元;……………… 6分
(3)中位数. ………………………………………………… 8分
19.证明:![]() 四边形BCC′D′为直角梯形,
四边形BCC′D′为直角梯形,


∴![]() …………2分
…………2分
∵Rt△ABC≌Rt△AB′C′,∴∠BAC=∠B′AC′.
∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°. 4分
(或:矩形ABCD绕点A旋转90°,AC旋转到AC′的位置,则∠CAC′=90°.)
(不证∠CAC′=90°的扣2分)
∴![]()
=![]() .……… 6分
.……… 6分
∴![]() , ∴
, ∴![]() .………… 8分
.………… 8分
20.解:过点A作DB的延长线的垂线AE,垂足为E.
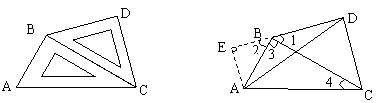

在等腰Rt△BDC中,∠1=45°设BD=DC=1,则BC=![]() …… 4分
…… 4分
在Rt△ABC中,∠4=30°,则AB=BC·tan30°=![]() .……6分
.……6分
在Rt△AEB中,∠2=180°-(∠1+∠3 )=180°-(90°+45°)=45°.
则EB=EA=AB·sin45°=![]() ·
·![]() =
=![]() .………… 8分
.………… 8分
在Rt△DEA中,DE=BD+EB=![]() +1,
+1,![]()
则cot∠ADB=![]() =
=![]() =
=![]() …… 10分
…… 10分
说明:在Rt△ABC中,设AB=1,以后计算正确的可相应给分.
21.解:设1台机组每小时处理污水v吨,要在5小时内处理完污水,至少需开动x台机组,则……………………………………………………………………………………… 1分
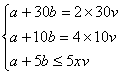 (①②各1分,③ 2分,其中③写成等式不扣分)… 5分
(①②各1分,③ 2分,其中③写成等式不扣分)… 5分
由得![]() ……………………………………………………… 7分
……………………………………………………… 7分
代入得![]() .…………………………………9分
.…………………………………9分
答:要在5小时内处理完污水,至少需同时开动7台机组. ……10分
22.证明:连结BC、OD,相交于点E.
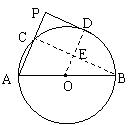

∵点D是![]() 的中点,则OD⊥BC,且BE=CE.………2分.
的中点,则OD⊥BC,且BE=CE.………2分.
∵∠ACB=∠APD=90°,∴PD∥BC.
∴OD⊥PD.∴PD为⊙O的切线.…………………… 4 分
且四边形PDEC为矩形.∴PD=CE=12.
∴BC=2CE=24…………………………………… 6分
又PD2=PC·PA,![]() =18.
=18.
∴AC=PA-PC=18-8=10.……………………… 8分
在Rt△ACB中,AB2=AC2+BC2=102+242=676
∴AB=26.∴⊙O的半径R=13.…………………… 10分
23.解:⑴如图,连结PB,过P作PM⊥x轴,垂足为M.
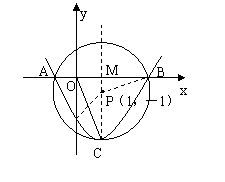

在Rt△PMB中,PB=2,PM=1,
∴∠MPB=60°,∴∠APB=120°…………………… 2分
![]() 的长=
的长=![]() ………………………… 4分
………………………… 4分
(2)在Rt△PMB中,PB=2,PM=1,则MB=MA=![]() .
.
又OM=1,∴A(1-![]() ,0),B(1+
,0),B(1+![]() ,0),
,0),
由抛物线及圆的对称性得知点C在直线PM上,
则C(1,-3). ………………………………………… 6分
点A、B、C在抛物线上,则
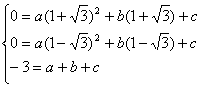 解之得
解之得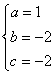
![]() 抛物线解析式为
抛物线解析式为![]() ………………… 8分
………………… 8分
(3)假设存在点D,使OC与PD互相平分,则四边形OPCD为平行四边形,且PC∥OD.
又PC∥y轴,∴点D在y轴上,∴OD=2,即D(0,-2).…………… 10分
又点D(0,-2)在抛物线![]() 上,故存在点D(0,-2),
上,故存在点D(0,-2),
使线段OC与PD互相平分.…………………………… 12分