初中升学招生考试数学试卷3
一、选择题（每小题4分共48分）
1. 据新华社报道，2003年我国税收首次突破20000亿元大关，用科学计数法表示应记为（ ）A、2×104亿元 B、20×103亿元 C、0.2×105亿元 D、2×105亿元
2. 圆柱的轴截面是（ ）A、等腰三角形 B、等腰梯形 C、矩形 D、圆
3.
已知
，那么下列等式中一定成立的是（ ）A、x=
y B、9x=7y C、7x=9y D、xy=63
4. 已知两圆的半径分别为7和3，圆心距为10，那么这两圆的位置关系是（ ）A、外切 B、内切 C、相交 D、内含
5. 抛物线y=（x－12）2+6的顶点坐标是（ ）A、（－12，6） B、（12，－6） C、（12，6） D、（－12，－6）
6.
有6张写有数字的卡片，它们的背面都相同，现将它们背面朝上（如右图），从中任意一张是数字3的概率是（ ）A、1/6 B、1/3 C、1/2 D、2/3
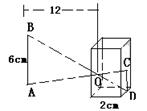
7. 右图是小孔成像原理的示意图，根据图中所标注的尺寸，这支蜡烛在暗盒中所成的像CD的长是（ ）A、1/6 cm B、1/3㎝ C、1/2㎝ D、1㎝
8.
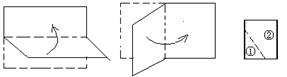将一张矩形纸片纸对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）A、三角形 B、矩形 C、菱形 D、梯形
9.
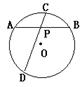如图，⊙O的弦AB、CD交于点P，已知P是AB的中点，AB=8cm，PC=2cm，那么PD的长是（ ）
Ａ、32㎝ B、8㎝ C、6 ㎝ D、2㎝
10.
在RtΔABC中，∠C=900，AC=6，sinB=2/3，那么AB的长是（ ）A、4 B、9 C、3
D、2
11. 方程（x2－3）2－5（3－x2）+2=0，如果设x2－3=y，那么原方程可变形为（ ）A、y2－5y+2=0 B、y2+5y－2=0 C、y2－5y－2=0 D、y2+5y+2=0
12. 下列图形中，不是立方体表面展开图的是（ ）
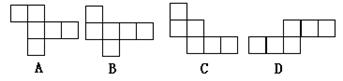
二、填空题（每小题5分共30分）
13.
计算：
（－1）= ；
14. 如果二次根式x2－ax+15在整数范围内可以分解因式，那么整数a的取（只需填写一个你认为正确的答案即可） 。
15.
如图有一个边长为1.5㎝的正六边形，如果要剪一张圆形纸片完全盖住这个图形，那么这张圆形纸片的最小半径为
cm。
16.
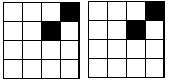由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）。请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称图形。
17.
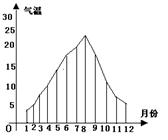
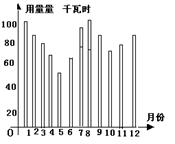图1表示某地区2003年12个月中每个月的平均气温，图2表示该地区某家庭这年12个月中每月的用电量。根据统计图，请你说出该家庭用电量与气温之间的关系（只要求写出一条信息即可）：
。
、
18. △ABO中，OA=OB=5，OA边上的高线长为4，将△ABO放在平面直角坐标系中，使点O与原点重合，点A在x轴的正半轴上，那么点B的坐标是 。
三、解答题（共72分）
19.
（8分）解方程
=5
20.
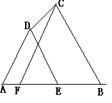
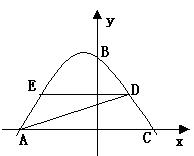（8分）如图在四边形ABCD中，DE∥BC，交AB于点E，点F在AB上，请你再添加一个条件（不再标注或使用其他字母），使△FCB∽△ADE，并给出出证明。你添加的条件是：。证明：
21. （9分）已知x1、x2是关于x的方程x2－2x+t+2=0的两个不相等的实数根。（1）求t的取值范围；（2）设S= x12+x22，求S关于t的函数关系式。
22. （9分）如图，已知抛物线经过点A（－3，0），B（0，3），C（2，0）三点。（1）求此抛物线的解析式；（2）如果点D（1，m）在这条抛物线上，求m的值的点D关于这条抛物线对称轴的的对称点E的坐标，并求出tan∠ADE的值。
23.
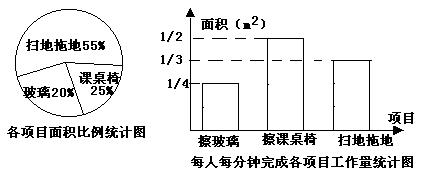（12分）某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80m2的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：（1）从上述统计图中可知：每人每分钟给擦课桌椅 m2；擦玻璃、擦课桌椅、扫地拖地的面积分别是 m2， m2， m2；（2）如果x人每分钟擦玻璃的面积是ym2，那么y关于x的函数关系式是
；（3）他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，该如何分配这两组的人数，才能最快地完成任务。
24.
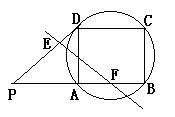（12分）已知：四边形ABCD为圆内接矩形，过点D作圆的切线DP，交BA的延长线于点P，且PD=15，PA=9。（1）求AD与AB的长；（2）如果点E为PD的一个动点（不与运动至P，D），过点E作直线EF，交PB于点F，并将四边形PBCD的周长平分，记△PEF的面积为y，PE的长为x，请求出y关于x的函数关系式；（3）如果点E为折线DCB上一个动点（不与运动至D，B），过点E作直线EF交PB于点F，试猜想直线EF能否将四边形PBCD的周长和面积同时平分？若能，请求出BF的长；若不能，请说明理由。
25.
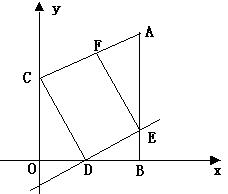（14分）如图在平面直角坐标系内，点A与C的坐标分别为（4，8），（0，5），过点A作AB⊥x轴于点B，过OB上的动点D作直线y=kx+b平行于AC，与AB相交于点E，连结CD，过点E作直线EF∥CD，交AC于点F。（1）求经过点A，C两点的直线解析式；（2）当点D在OB上移动时，能否使四边形CDEF成为矩形？若能，求出此时k、b的值；若不能，请说明理由；（3）如果将直线AC作向上平移，交Y轴于点Cˊ，交AB于点Aˊ，连结DCˊ，过点E作EFˊ∥DCˊ，交AˊCˊ于点Fˊ，那么能否使四边形CˊDEFˊ成为正方形？若能，请求出此时正方形的面积；若不能，请说明理由。