第二课 实数的运算
知识点:有理数的运算种类、各种运算法则、运算律、运算顺序、科学计数法、近似数与有效数字、计算器功能鍵及应用。
大纲要求:
1.了解有理数的加、减、乘、除的意义,理解乘方、幂的有关概念、掌握有理数运算法则、运算委和运算顺序,能熟练地进行有理数加、减、乘、除、乘方和简单的混合运算。
2.了解有理数的运算率和运算法则在实数运算中同样适用,复习巩固有理数的运算法则,灵活运用运算律简化运算能正确进行实数的加、减、乘、除、乘方运算。
3.了解近似数和准确数的概念,会根据指定的正确度或有效数字的个数,用四舍五入法求有理数的近似值(在解决某些实际问题时也能用进一法和去尾法取近似值),会按所要求的精确度运用近似的有限小数代替无理数进行实数的近似运算。
4 了解电子计算器使用基本过程。会用电子计算器进行四则运算。
考查重点:
1.考查近似数、有效数字、科学计算法;
2.考查实数的运算;
3.计算器的使用。
实数的运算
(1)加法
同号两数相加,取原来的符号,并把绝对值相加;
异号两数相加。取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值;
任何数与零相加等于原数。
(2)减法 a-b=a+(-b)
(3)乘法
两数相乘,同号得正,异号得负,并把绝对值相乘;零乘以任何数都得零.即
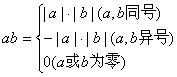
(4)除法 ![]()
(5)乘方 ![]()
(6)开方 如果x2=a且x≥0,那么![]() =x; 如果x3=a,那么
=x; 如果x3=a,那么![]()
在同一个式于里,先乘方、开方,然后乘、除,最后加、减.有括号时,先算括号里面.
3.实数的运算律
(1)加法交换律 a+b=b+a
(2)加法结合律 (a+b)+c=a+(b+c)
(3)乘法交换律 ab=ba.
(4)乘法结合律 (ab)c=a(bc)
(5)分配律 a(b+c)=ab+ac
其中a、b、c表示任意实数.运用运算律有时可使运算简便.
典型题型与习题
一、填空题:
1.我国数学家刘徽,是第一个找到计算圆周率π方法的人,他求出π的近似值是3.1416,如果取3.142是精确到 位,它有 个有效数字,分别是 。
1.5972精确到百分位的近似数是 ;我国的国土面积约为平方干米,用科学计数法表示为 平方干米。
2.按鍵顺序-1·2÷4=,结果是 。
3.我国1990年的人口出生数为人。保留三个有效数字的近似值是
人。
4.由四舍五入法得到的近似数3.10×104,它精确到 位。这个近似值的有效数字是 。
5.2的相反数与倒数的和的绝对值等于 。
6.若n为自然数时(-1)2n+1+(-1)2n= .
7.查表得2.132=4.5,4.1053=69.18,则-21.32= 。(-0.0213)2= ,0.41053= ,-(-410.5)3= 。若8.3202=69.32,x2=6.932×105,则x= .=2.107 =6.663 = .
8.已知2a-b=4, 2(b-2a)2-3(b-2a)+1=
9.已知:|x=4,y2=且x>0,y<0,则x-y= 。
二、选择题
1. 下列命题中:(1)几个有理数相乘,如果负因数个数是奇数,则积必为负;
(2)两数之积为1,那么这两数都是1或都是-1;(3)两个实数之和为正数,积为负数,则两数异号,且正数的绝对值大;(4)一个实数的偶次幂是正数,那么这个实数一定不等于零,其中错误的命题的个数是( )
(A)1 个 (B)2 个 (C)3个 (D)4个
2.近似数1.30所表示的准确数A的范围是( )
(A)1.25≤A<1.35 (B)1.20<A<1.30
(C)1.295≤A<1.305 (D)1.300≤A<1.305
3.设a为实数,则a+a运算的结果( )
(A) 可能是负数(B)不可能是负数(C)一定是负数(D)可能是正数。
4.已知a=8,b=2,a-b=b-a,则a+b的值是( )
(A) 10 (B)-6 (C)-6或-10 (D)-10
5.绝对值小于8的所有整数的和是( )
(A)0 (B)28 (C)-28 (D)以上都不是
6.由四舍五入法得到的近似数4.9万精确到( )
(A)万位 (B)千位 (C)十分位 (D)千分位
7. 计算下列各题:
(1) 32÷(-3)2+- ×(- 6)+;
(2) {2(-)-× ÷}×(-6);
(3)-0.252÷(-)4+(1+2-3.75)×24;
(4){-3()2-22 ×0.125-(-1)3÷}÷{2×(-)2-1}。
(5){×(-2)2-()2+}÷ 21996·(-)1995 .
(6)
(7)0.3-1-(- )-2+43-3-1+(π-3)0+tg2300
(8)()-1-(2001+ctg300)0+(-2)2···+