第二十八课 锐角三角函数
〖知识点〗
锐角三角函数、锐角三角函数值的符号、锐角三角函数值的变化规律、特殊角三角函数值、互为余角的三角函数间的关系、同角三角函数间的关系（平方关系、商数关系、倒数关系）
〖大纲要求〗
1． 理解正弦、余弦、正切、余切的概念，并能运用；
2． 掌握正弦和余弦表、正切和余切表的查法，掌握特殊角三角函数值，并能运用特殊角的三角函数值进行计算和化简；
3． 掌握互为余角和同角三角函数间关系，并能运用它们进行计算或化简。
〖考查重点与常见题型〗
1． 求三角函数值，常以填空题或选择题形式出现，如：
在Rt△ABC中，∠C＝90°，3a＝b，则∠A＝ ，sinA＝
2． 考查互余或同角三角函数间关系，常以填空题或选择题形式出现，如：
(1) sin53°
cos37°＋cos53°sin37°＝
(2) 在Rt△ABC中，∠C＝90°，下列各式中正确的是（ ）
(A)sinA＝sinB (B)sinA＝cosB (C)tanA＝tanB (D)c0tA＝cotB
3． 求特殊角三角函数值的混合运算，常以中档解答题或填空题出现，如：
1－2sin30°cos30°＝
〖预习练习〗
1．Rt△ABC中，若sinA＝，AB＝10，那么BC＝ ，tanB＝
2．若tanα·tan16°＝1，且α为锐角，则α＝
3．写出适合条件的锐角α
cosα＝,α= ,tan2α－4tanα＋＝0，则α＝
4． 查表求cot68°19ˊ时，先查得cot68°18ˊ＝0.3979，又查得1ˊ的修正值是0.0003，则cot68°19ˊ＝
5． 设α、β互为余角，则tanα·tanβ－cot＝
6． 直角三角形中，∠C＝90°，a，b分别是A，B的对边，则是角A的（ ）
（A）正弦 （B）余弦 （C）正切 （D）余切
7． △ABC中，∠C＝90°，则cosA·cotB的值是（ ）
（A） （B） （C） （D）
考点训练
1．Rt△ABC中，∠C＝90°，AB＝6，AC＝2，则sinA＝（ ）
（A） （B） （C） （D）
2．在△ABC中，∠C＝90°，sinA＝，则tanA·cosA的值是（ ）
（A） （B） （C） （D）
3．已知∠A＋∠B＝90°，则下列各式中正确的是（ ）
（A）sinA＝sinB (B)cosA＝cosB (C)tanA＝cogB (D)tanA＝tanB
4．若0°<a<45°，则下列各式中正确的是（ ）
（A）sina>cosa (B)cosa>sina (C)cota<1 (D)tana>cota
5．Rt△ABC中，∠C＝90°，AC∶BC＝1∶，则cosA= ，cotA＝
6．设a为锐角，若sina＝，则a＝ ，若tana＝，则a＝
7．查表得cot56°42ˊ＝1.5224，2ˊ的修正值为0.0019，则cot56°44ˊ＝
8．已知a为锐角，若cosa＝，则sina＝ ，tan(90°－a)＝
9. 已知sina=, a为锐角，则cosa＝ ，tana＝ ，cota＝
10．用“>”或“<”连结：
cos18° cos18°3ˊ； tan31° tan32°； tan29°30ˊ cot60°29ˊ
sin39° cos51°；cot30° sin89°；sina＋cosa 1（a为锐角）
11．计算：（1）sin60°＋ cos45°＋sin30°·cos30°
（2）3 tan30°－＋cos0°·cos45°
12．△ABC中，∠BAC＝90°，AD是高，BD＝9，tanB＝，求AD、AC、BC
13．已知方程x2－5x·sina＋1＝0的一个根为2＋，且a为锐角，求tana
的值。
解题指导
1． 计算：（1）sin45°·cos45°＋＋3cot260°+
（2）
2． 若a为锐角，tga＝3，求的值。
3． 在Rt△ABC中，∠C＝90°，求证：a3cosA＋b3cosB=abc
4． 方程x2－x ＋m＝0的两根是一个直角三角形中两锐角的余弦cosA和cosB，求A、B的度数和m的值。
5． 若方程2x2－2x·cosa＋cosa（cosa＋4）＝0的两个根x1、x2满足（x1－1）（x2－1）＝，求sina的值。
6．△ABC中，AB＝AC，∠BAC＝36°，AD是BC边上的高，BE是∠ABC的平分线，BC＝1，试利用这个三角形求出sin18°的值。
7．已知sinθ和cosθ是方程a2x2＋a3x＋1＝0的两根，求a的值。
独立练习
1．在Rt△ABC中，∠C＝90°，sinA∶sinB＝3∶4，则ctgA的值（ ）
（A） （B） （C） （D）
2．若2cosa－＝0，则锐角a＝（ ）
（A） 30°（B）15° （C）45°（D）60°
3． 已知a=sin25°，b=tan46°，c=cot17°，m=cos20°，则a、b、c、m的大小关系（ ）
（A） a<b<c<m（B）b<m<c<a（C）a<m<b<c（D）m<a<b<c
4．在Rt△ABC中，各边的长度都扩大两倍，那么锐角A的各三角函数值（ ）
（A） 都扩大两倍（B）都缩小两倍（C）没有变化（D）不能确定
5．0°<a<45°，下列不等式中正确的是（ ）
(A)cosa<sina<cota（B）cosa<cota<sina（C）sina<cosa<cota（D）cota<sina<cosa
6．Rt△ABC中，∠C＝90°，b∶a＝1∶，则cosB= ,cotA＝
7．已知锐角a的终边经过点P（x，2），点P到坐标原点的距离r＝,则sina= ，cosa＝
8．查表求cos43°26ˊ的值时，先查得cos43°24ˊ＝0.7266，又查得2ˊ的 修正值为0.0004，那么cos43°26ˊ＝
9．5sin2(90°－a)＋5sin2a＝
10．计算：
（1）＋（2）cos21°＋cos22°＋···＋cos288°＋cos289°
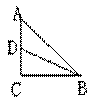11．已知△ABC中，∠C＝90°，∠A＝45°，BD为AC边上中线，求sin∠ABD和tan∠ABD的值。
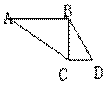
12．如图，∠ABD＝∠BCD＝90°，AB＝8，sinA＝，CD＝2，求∠CBD的四个三角函数值。
 |