第二十九课 解直角三角形
〖知识点〗锥度、坡度、仰角、俯角、方位角、方向角、解直角三角形、解直角三角形应用
〖大纲要求〗
1.理解直角三角形的概念及锥度、仰角和俯角、坡度和坡角、方向角和方位角的概念，灵活运用直角三角形中边与角的关系和勾股定理解直角三角形，提高把实际问题转化为解直角三角形问题的能力；
2.掌握三角形的面积公式S＝absinа；
3.理解正多边形的概念和性质，会画简单的正多边形，能将正多边形的边长、半径、边心距和中心角的有关计算转化为解直角三角形；
4.利用锐角三角函数和直角三角形，把“数”和“形”互相转化解决某些问题，用数形结合的重要数学思想指导本章解各类习题，通过添加适当的辅助线构造直角三角形把非直角三角形问题转化为解直角三角形的问题，使之得以解决，这些转化的思想值解数学题的重要数学思想，掌握综合性较强的题型融会贯通地运用数学的各部分知识，提高分析解决问题的能力。
〖考查重点与常见题型〗 近三年的中考题中多见解直角三角形的应用
〖预习练习〗
1．△ABC中，∠C＝90°，根据表中的数据求其它元素的值：
| a | b | c | ∠A | ∠B |
| 12 | 30° | |||
| 4 | 45° | |||
|
| 60° | |||
| 5 | 5 | |||
| 4 | 8 |
2.在Rt△ABC中，AD是斜边BC上的高，如果BC＝a，∠B＝α，那么AD等于（ ）
(A)asin2α (B)acos2α (C)asinαcosα (D)asinαtanα
3．半径为10cm的圆内接正三角形的边长为 ，内接正方形的边长为 ，内接正六边形的边长为
4.已知正六边形的面积为3cm2，则它的外接圆半径为
5.已知△ABC中，∠B＝30°，a＝2，c＝3，则S△ABC＝
6.等腰三角形的腰长为2cm，面积为1 cm2，则顶角的度数为
7.已知一山坡的坡度为1:3，某人沿斜坡向上走了100m，则这个人升高了 m
8.一锥形零件的大头直径为20cm，小头直径为5cm，水平距离为35cm，则该锥形零件的锥度为
考点训练：
1.在Rt△ABC中，∠C=90°，已知a和A，则下列关系中正确的是( )
(A) c=asinA ( B) c= (C) c=acosA (D) c=
2．在Rt△ABC中，∠C=90°，c=10 ∠A=30°，则b=（ ）
(A) 5 (B) 10 (C) 5 (D) 10
3. 在Rt△ABC中，∠C=90°，AB的坡度i=1：2,则BC：CA：AB等于( )
(A) 1：2：1 (B) 1： ：2 (C) 1： ： (D) 1：2：
4.从1.5m高的测量仪上,测得某建筑物顶端仰角为30°,测量仪距建筑物60m,则建筑物的高大约为( )
A 34.65m B 36.14m C 28.28m D 29.78m
5.已知直角三角形中,较大直角边长为30,此边所对角的余弦值为，则三角形的周长为 ，面积为 。
6.在平行四边形ABCD中，AD：AB=1：2,∠A=60°,AB=4cm,则四边形面积为
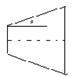
7.一锥形零件的表面如图，图纸上规定锥度k=3：8，则斜角a的正切值为
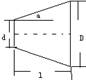8.在△ABC中, ∠C=90°, ∠A 、∠B、∠C所对的边分别为a、b、c.
(1)若∠A=60°,a+b=3+,求a、b、c及S△ABC
(2)若△ABC的周长为30,面积为30,求a、b、c
 |
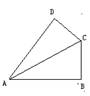9.如图四边形ABCD中, ∠A=60°, ∠B=∠D=90, CD=2, BC=11,
求AC的长
10.从高出海平面500米的直升飞机上,测得甲乙两船的俯角分别为45°和30°,已知两船分别在正东和正西,飞机和两船在同一铅垂面内,求两船的距离.
解题指导(1)
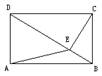
1. 在矩形ABCD中,CE⊥BD,E为垂足,连结AE,已知BC=3,CD=4,
求(1)△ADE的面积,
(2)tan∠EAB
2．已知∠MON＝60°，P是∠MON内一点，它到角的两边的距离分别为2和11，求OP的长
3．一个圆内接正三角形面积为16cm2,求(1)这个圆的半径；(2)这个圆的外切正三角形面积?
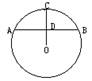
4．如图,已知⊙O中弦AB=2,弓形高CD=2-,求弓形ABC的面积
5.若a、b、c是△ABC的三边, a+c=2b,且方程a(1- x2)+2bx+c(1+ x2)=0有两个相等的实数根,求sinA+sinB+sinC的值
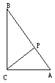6.如图,在Rt △ABC中,∠ACB=Rt∠,AC=2,tan2A+ tan2B=
,∠A>∠B,点P在斜边AB上移动,连结PC,(1)求∠A的度数(2)设AP为x,CP2为y,求y关于x的函数表达式及自变量x的取值范围,(3)求证：AP=1时,CP⊥AB
四．解题指导（2）
1.（1）已知锥体轴截面(如图)，斜角α,tanα=，求锥度K=
（2）一锥形零件锥度为，小头直径为20mm，长为64mm,求这个零件侧面积；
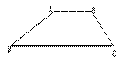
（3）如图，渠道横截面为等腰梯形，内坡比为2：1，测得距深为2m，上口宽为3.5m，求渠道底宽。
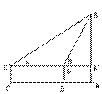
2.如图，某海埂的横断面是梯形，坎上底AD为4米，近水面（斜坡AB）的坡度i=1：，斜坡AB的长度为12米，背水面（斜坡CD）的坡度为i=1：1，求（1）斜坡AB的坡角（2）坎底宽BC和斜坡CD的长。
3.要测得底部不能到达的烟囱的高AB，从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β，CD间的距离是a米，已知测角仪的高b米，求烟囱的高AB
4.某海轮以每小时30海里的速度航行，在A处测得海面上油井P在南偏东60°，一直向北航行40分钟后到达B点，测得油井P在南偏东30°。海轮改为北偏东60°的航向再航行80分钟到达C点（1）画出海轮航行的示意图（2）试求P、C 间的距离（结果可保留根号）
5..如图，A城气象台测得台风中心从A城正西方向300千米B处以每小时10千米的速度向北偏东60°的BF方向移动，距台风中心200千米的范围内为受台风影响的区域（1）问A城是否会受这次台风的影响？并说明理由（2）若A城受到这次台风的影响，那么A城遭受这次影响的时间有多少长？
独立练习：
1.在Rt△ABC中，∠C=90°，cosB=，则a:b:c=（ ）
(A) 2：：3 (B) 1：2：3 (C) 1：：3 (D) 2：：
2. 在Rt△ABC中，∠C=90°，斜边中线是3cm，sinA=，则S△ABC=（ ）
(A) cm2 (B) 2cm ( C ) 3cm2 ( D) 4cm2
2. 在Rt△ABC中，∠C=90°，AB=50，AC=50，则BC= ，∠B= ，S△ABC=
4. 在Rt△ABC中，两条直角边之比为2：3，斜边长为3，则最小角的余弦值是
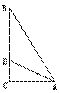5.已知，如图△ABC中，∠ C=90°，AD平分∠BAC，CD=，BD=2，求平分线AD的长，AB，AC的长，外接圆的面积，内切圆的面积。
6．已知△ABC中，AD⊥BC于D，点E在AC上，且∠B=∠DEC，=(1）求∠C的度数（2）若CD=2，S△ABC=6，求AB的长
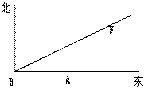
7.一船从西向东航行，航行到灯塔C处，测得海岛B在北偏东60°方向，该船继续向东航行到达灯塔D处时，测得海岛B在北偏东45°方向，若灯塔C、D间的距离是10海里，海岛B周围12海里有暗礁，问该船继续航行（沿原方向）有无触礁的危险？
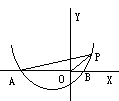8.如图，二次函数y=x2+bx+c的图像与x轴相交于A,B，点A在原点左边，点B在原点右边，点P（1，m）（m>0）在抛物线上，AB=2，
tan∠PAB=,（1）求m的值；（2）求二次函数解析式