第20课 等腰三角形
〖知识点〗
等腰三角形、等腰三角形的性质和判定、等边三角形、等边三角形的性质
和判定、轴对称、轴对称图形
〖大纲要求〗
1． 理解等腰三角形的概念，掌握等腰三角形的两底角相等、等腰三角形三线合一等性质，掌握两个角相等的三角形是等腰三角形等判定定理，并能运用它们进行简单的证明和计算；
2． 理解等边三角形的概念，掌握等边三角形的各角都是60°等性质，掌握三个角都相等的三角形或一个角是60°的等腰三角形都是等边三角形等判定，能运用它们进行简单的证明和计算；
3． 了解轴对称及轴对称图形的概念，会判断轴对称图形。
〖考查重点与常见题型〗
等腰三角形和等边三角形的性质和判定的应用，证明线段、角相等，求线
段的长度、角的度数，中考题中多以选择题、填空题为主，有时也考中档
解答题，如：
（1）如果，等腰三角形的一个外角是125°，则底角为 度；
（2）等腰三角形一腰上的高与底边的夹角为45°，则这个三角形是（ ）
A．锐角三角形 B．钝角三角形 C．等边三角形 D．等腰直角三角形
〖预习练习〗
1．一个正三角形的边长为a，它的高是（ ）
（A） （B） （C） （D）
2．如果等腰三角形一腰长为8，底边长为10，那么连结这个三角形各边的
中点所成的三角形各边的中点形成的三角形的周长为（ ）
（A）26 （B）14 （C）13 （D）9
3．等腰直角三角形的一条直角边为1cm，则斜边上的高为
4． 若等腰三角形的底角为15°，腰长为2，则腰上的高为
5． 已知等腰三角形的一边等于4cm，一边等于9cm，那么它的周长等于 cm
6．
等腰三角形的底边长为3，周长为11，则一腰长为
7． 等腰三角形的周长为2＋，腰长为1，底角等于 度
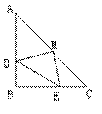
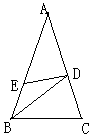
8． 已知如图，在△ABC中，∠B＝90°，AB＝BC， BD＝CE，
M是AC的中点，求证：△DEM是等腰三角形
考点训练
1．等腰三角形周长是29，其中一边是7，则等腰三角形的底边长是（ ）
（A）15 （B）15或7 （C）7 （D）11
2．在△ABC中，AB＝AC，BD平分∠ABC，若∠BDC＝75°，则∠A的度数为（ ）
（A）30° （B）40° （C）45 ° （D）60°
3．等腰△ABC的顶角∠A＝15°，P是△ABC内部的一点，且∠PBC＝∠PCA，则∠BPC的度数为（ ）
（A）100° （B）130° （C）115 ° （D）140°
4．等腰三角形的对称轴有（ ）
（A）1条 （B）2条 （C）3条 （D）1条或3条
5．在△ABC中，AB＝AC，用∠A表示∠B，则∠B＝
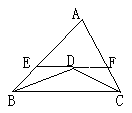
6．如图，CD、BD平分∠BCA及∠ABC，EF过D点且EF∥BC，
则图中的等腰三角形有 个，它们是
7．如图△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC，
DE⊥AB于E，则∠C＝ ，∠BDE＝ ，
AE＝ ；若△BDC周长为24，CD＝4，则BC＝ ，
△ABD的周长为 ，△ABC的周长为
8． 等腰三角形一腰上的中线把这个三角形的周长分为15厘米和
11厘米两部分，则此三角形的底边长为
9． 
如图，等腰三角形ABC中，AB＝AC，∠A＝90°，BD平分∠ABC，DE⊥BC且BC＝10，求△DCE的周长。
10．等边三角形ABC中，D是AC中点，E为BC延长线一点，且DB＝DE，求证：
△ DCE是等腰三角形。
解题指导
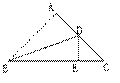
1． 
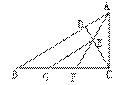如图，在△ABC中，∠ACB＝90°，CD⊥AB于D，AF平分∠BAC交CD于E，交BC于F，EG∥AB交BC于G，求证：BG＝CF。
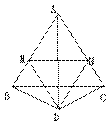2.已知如图△ABC是边长为a的等边三角形，△BCD的顶角∠BDC＝120°，DB＝DC以D为顶点作一个60°的角，角的两边DM、DN分别交AB于M，交AC于N，
连结MN，求△ABD的周长。
 |
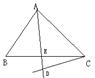3.如图在△ABC中，AE平分∠BAC，∠DCB＝∠B－∠ACB，
求证：△DCE是等腰三角形。
4.如图在△ABC中，CD⊥AB于D，且E、F、G分别是AC、BC、AB的中点，
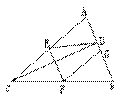求证：∠DEF＝∠BGF
独立训练
1．
在△ABC中，∠B＝36°，D、E在BC边上，且AD和AE把∠BAC三等分，则图
中等腰三角形的个数（ ）
（A）3 （B）4 （C）5 （D）6
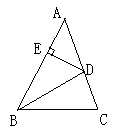
2．如图，在△ABC中，AB=AC，BD=BC，AD=DE=EB，
则∠A等于（ ）
（A）30° （B）36° （C）45 ° （D）54°
3．等腰三角形的一个内角为70°，它的一腰上的高与底边所夹的
角的度数是（ ）
（A）35° （B）20° （C）35 °或 20°（D）无法确定
4．等腰三角形的顶角等于一个底角的3倍，则顶角的度数为 ，底角的度数为
2． 等腰三角形三个内角与顶角的外角之和等于260°，则它的底角度数为
3． 等腰△ABC中，AB=AC，BC=6cm，则△ABC的周长的取值范围是
7．如图，等边△ABC中，O点是∠ABC及∠ACB的角平分线的交点，OM∥AB
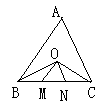交BC于M，ON∥AC交BC于N，求证：M、N是BC的三等分点。
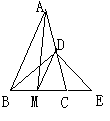8．已知△ABC中，AB=AC，D、M分别为AC、BC的中点，E为BC延长线上一点，且CE=BC，求证：（1）∠DMC=∠DCM；（2）DB=DE
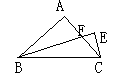9．如图，在△ABC中，∠A＝90°，且AB=AC，BE平分∠ABC交AC于F，过C作BE的垂线交BE于E，求证：BF=2CE
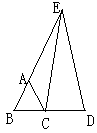10.如图，△ABC为等边三角形，延长BC到D，延长BA到E，AE=BD，
连结EC、ED，求证：CE=DE