说明:
本试卷中的抛物线、双曲线等图形是用几何画板画的。如何在word中准确画函数的图象，如部分抛物线、不对称抛物线、双曲线等等，使试卷图形更加准确、美观，是制卷者共同的目标。如果你有兴趣，可到本人k12的
个人专辑
上下载相关的工具，有什么更好的方法，欢迎交流、指导。
初三数学月考试卷
班级 编号 姓名
一、填空题（每小题2分，共30分）
1、点（-1，3）在第 象限。
2、函数
自变量x的取值范围为
。
3、点（
）关于x轴对称的点的坐标为（ ， ）。
4、直线
与y轴的交点坐标是（ ， ）。
5、圆的内接平行四边形是 形。
6、对于函数
，当x＜0时,y随x的增大而 。
7、当m= 时，函数
是反比例函数.
8、抛物线
的顶点坐标是（ ， ）。
9、等腰三角形周长为20cm，腰长为x(cm),底边长为y(cm),则y与x的函数关系式为 ,自变量x的取值范围是 。
10、自圆外一点向圆所引两条切线的夹角为60°,若切线长为5cm,则此圆的半径为 cm.
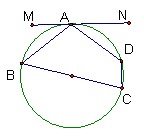
11、如图，四边形ABCD内接于⊙O，BC是直径，MN切⊙O于点A，
∠MAB=35°，则∠B=_______度.
第11题 第12题 第14题
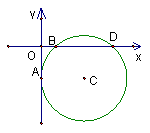
12、如图，在直角坐标系中，⊙C与y轴相切与x轴相交于（1, 0），（5, 0）两点，圆心C在第四象限，则C点坐标为 。
13、将抛物线
向左平移一个单位，再向上平移3个单位得到抛物线，其解析式为
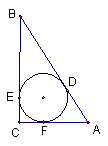
14、如图，在Rt△ABC中，⊙O分别切AB、BC、AC于D、E、F三点，AB=10，∠A的余弦值为
，则S⊙O=
15、点P不在⊙O上，过P的直线交⊙O于AB，若
，OP=5，则⊙O的半径长为
。
二、选择题（每小题3分，共24分）
16、点P 在第二象限，且P点到x轴的距离为3, 到y轴的距离为2, 则P点坐标为 （ ）
A 、（2, -3） B、（3, -2） C、（－2, 3） D、（－3, 2）
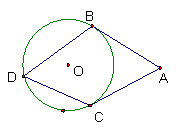
17、已知如图，AB、 AC分别切⊙O于B、C两点，点D 是⊙O上一点，
∠D＝400，则∠A的度数为 （ ）
A、1400 B、1200 C、1000 D、800
第17题 第18题
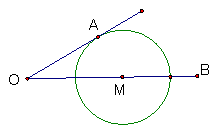
18、如图，已知∠AOB=300，M为OB上一点，且OM＝5cm, 以M为圆心与直线OA有且只有一个交点的圆的半径r长为 （ ）
A、2cm B、3cm C、2.5cm D、3.5cm
19、已知一次函数
，如果y随x的增大而减小，则它的图像经过（ ）
A、第二、三、四象限 B、 第一、二、三象限
C、第一、三、四象限 D、 第一、二、四象限
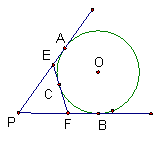
20、如图，P 为⊙O外一点，PA 、PB切⊙O于A、B，PA=PB=4cm，EF切⊙O于C交PA、PB于E、F，则△PEF的周长等于 （ ）
A、4cm B、8cm C、12cm D、16cm
21、如图，⊙O的两条弦AB、CD相交于点E，AC和BD的延长线交于点P，下列结论成立的是 （ ）
A、PB·PD=PC·PA B、PC·AC=PB·BD
C、CE·AE=BE·ED D、CE·CD=BE·BA
第20题 第21题
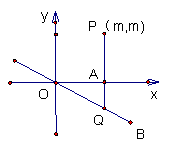
22、已知函数
的图象如图所示，过点
，平行y轴的直线交
x轴于A，交的图象于点Q，若AP
AQ，则k的取值范围 （ ）
A、k＞0 B、k＜0 C、
＜k＜0 D、 k＜
第22题 第23题
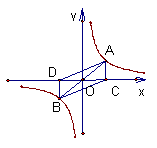
23、如图A、B是函数
的图象上关于原点对称的任意两点AC∥y轴x
交轴于点C，BD∥y轴交x轴于点D，设四边形ADBC的面积为S，则（ ）A、S = 1 B、1＜S＜2 C、S = 2 D、S＞2
三、解答、证明题（共76分）
24、（本题6分）已知线段a、b，
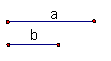求作线段c，使
作法：
25、（本题6分）已知：如图，⊙O1、⊙O2相交于A、B，PE切⊙O1于P，PA、PB交⊙O2于C、D。求证：CD∥PE。
26、（本题8分）已知
，且
与
成正比例，
与
成反比例，当x=1时，
，当x=3时，y=5。
（1）求y关于x的函数解析式；
（2）求当
时，y的值。
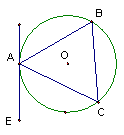
27、（本题8分）已知：如图，⊿ABC内接于⊙O，AB为非直径的弦，∠CAE=∠B，求证：AE与⊙O相切于A。
28、（本题8分）
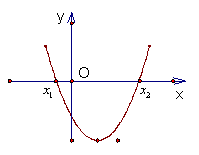
І、设二次函数
（
）与x轴有两个交点A（
）、B（
）（
），不妨设
，其图象如图所示
（1）当y=0，即
，所以方程的解是：
或
；
（2）当y>0，即
，所以不等式的解集是
或
；
（3）当y<0，即即
，所以不等式的解集是
；
П、在І中，若
，解下列不等式（直接填结果）
（1）不等式的解集是
；
（2）不等式的解集是
。
Ш、利用上述结论，写出不等式的解集：
（1）
的解集
；
（2）
的解集
。
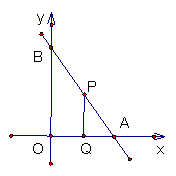
29、（本题8分）如果直线l与x轴、y轴的正轴分别交于A、B两点，OA、OB的长分别是关于x的方程
的两根（OB>OA），P为直线l上A、B两点之间的一动点（不与A、B重合），PQ∥OB。
（1）求tan∠BAO的值；
（2）若
时，请确定点P在AB上的位置，并求出线段PQ的长。
30、（本题10分）某产品每件的成本是120元，试销阶段每件产品的销售价x（元）与产品的日销售量y（台）之间的关系如下表，并且日销售量y是每件产品销售价x的一次函数。
| x（元） | 130 | 150 | 165 |
| y（台） | 70 | 50 | 35 |
（1）求y与x的函数关系式；
（2）若销售利润用S表示，为获得最大销售利润，每件产品的销售价应定为多少元？此时每日的销售利润是多少？
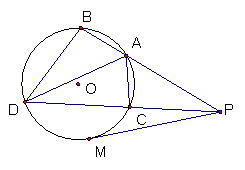
31（本题10分）已知：如图，PM是⊙O的切线，M为切点，PAB和PCD均是⊙O的割线，它们与⊙O的交点分别为A、B、C、D，且
。
求证：（1）∠DAP=∠BAC；
（2）⊿PAC∽⊿DAB；
（3）
证明(3)
证明(1)
证明(2)
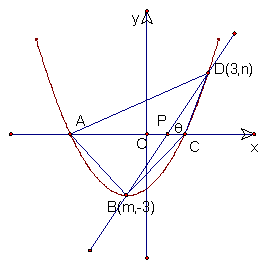
32、（本题12分）如图，直线L与x轴相交于点P（1、0），与x轴所夹的锐角为θ，且
=
，直线L与抛物线y=
x2+bx+c(a>0)相交于点B
,D
。（1）求B、D两点的坐标，并用含a的代数式表示b和c。
（2）（i）若关于x的方程x2+
ax+a2-
a+
=0有实根,求此抛物线的解析式；
（ii）若抛物线y=x2+bx+c(a>0)与x轴相交于A、C两点，顺次连结A，B，C，D得凸四边形ABCD，问四边形ABCD的面积S有无最大值或最小值？若有求S的最大值或最小值？若无，请说明理由。
解(2) （i）
解(1)
解(2)（ii）