初三数学诊断试题
班级______ 姓名 学号______
A卷 （满分100分）
一． 选择题（每题4分，共60分）
1．下列运算中正确的是（ ）
A．（–1）
=-1 B.3
=-9 C.(
)
=a D.∣-a∣=a
2.如果一组数据6，X，2，4，的平均数为5，则X等于（ ）
Ａ.5 B.6 C.7 D.8
3.在二次根式
，
，
，
，
中最简二次根式的个数是（ ）
A．１个 Ｂ.2个 Ｃ.３个 Ｄ.４个
４．下列图形中，既是中心对称图形，又是轴对称图形的是（ ）
Ａ.角 Ｂ.线段 Ｃ.等边三角形 Ｄ平行四边形
５．抛物线y=–2(x+4)–9 的顶点坐标和对称轴方程分别是（ ）
Ａ.（４，–９）对称轴x=4 B.(–4, 9)对称轴x=–４
C.(–4,–9)对称轴x=4 D.(–4,–9)对称轴x=–4
6．方程2x
+3x–4=0的根的情况是（ ）
A．两不等实根 B.两相等实根 C.一个实根 D.无实根
7．已知函数y=(m–1)x
是反比例函数，则m的值为（ ）
A．1
B.–1 C.±1 D.±
8．关于x的一元二次方程x+kx+3=0的一个根为–1，则k的值是（ ）
A．–3 B.–4 C.4 D.2
9．圆内接四边形MNPQ中，∠M，∠N，∠P的度数比是3∶4∶6，则∠Q的度数是（ ）
A． 60° B.80° C.100° D.120°
10．如果k＜0，那么下列说法中正确的是（ ）
A．函数y=kx 中y随x增大而增大
B．函数 y=
的图象的两个分支分别位于第一.三象限内
C．抛物线y=(x+k)的对称轴是x=k
D. 直线 y=kx+k经过第二、三、四象限
11.一个多边形内角、外角之和为2160°，则这个多边形的边数是（ ）
A．14 B.12 C.10 D.8
12.在函数y=
+
中自变量x的取值范围是
A．x＞0且x≠－1 B.x≥0且x≠-1 C.x＜0且x≠-1 D.x≤0且x≠-1
13．正六边形的半径为R，则它的边心距为（ ）
A.
R B.
R C.
R
D.
R
14．某商品进价为 a元，现将进价提高20%作为售价,又将售价的90%作为优惠价出售,则该商品能盈利 ( )
A .0.08a B.0.10a C.0.12a D 0.14a
15. 圆锥的底面直径为６，侧面积为１５
，则圆锥的高是（ ）
Ａ.5 B.4 C.3 D.6
二、解答下列各题：（每小题６分，共１２分）
１．计算 
＋cos30°+
-(-2)
2.先化简，再求值：
÷
－
，其中x=－
三、解答下列各题：（每小题６分，共１２分）
１．
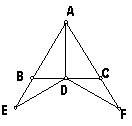已知：如图，ΔＡＢＣ中ＡＢ＝ＡＣ，ＡＤ⊥ＢＣ，垂足是Ｄ，Ｅ、Ｆ分别是ＡＢ、ＡＣ延长线上的点，且ＢＥ＝ＣＦ.
求证：ＤＥ＝ＤＦ
２．一船以每小时３６海里的速度向正北航行到Ａ处，发现它的东北方向有一灯塔Ｂ，船继续向北航行４０分钟后到达Ｃ处，发现灯塔Ｂ在它的北偏东７５°方向，求此时船与灯塔的距离.
四、列方程（组）解应用题（８分）
Ａ、Ｂ两地相距８７公里，甲骑自行车由Ａ向Ｂ行驶３０分钟后，乙骑自行车由Ｂ出发，用比甲每小时快４公里的速度向Ａ行驶，二人在距Ｂ４５公里处相遇，求甲乙二人骑自行车的速度.
五、（８分）如图，ＡＢ为⊙Ｏ的直径，Ｃ是⊙Ｏ上一点，过点Ｃ的切线与ＡＢ的延长线相交于点Ｅ，ＡＤ⊥ＥＣ，垂足为Ｄ，且ＡＤ交⊙Ｏ于点Ｆ.
求证: （１）ＢＣ＝ＣＦ
（２）ＥＣ·ＣＤ＝ＥＢ·ＤＡ
B 卷 （５０分）
一、填空（１５分）
１．化简：ａ
＝
２．
已知Ａ是双曲线
在第二象限内的分支上的点，ＡＢ⊥ｘ轴于Ｂ，Ｏ为坐标原点，且Ｓ
＝３，则Ｋ＝
３．如图，ＡＤ是△ＡＢＣ的中线，∠ＡＤＣ＝４５°，
ＢＣ＝４，把△ＡＤＣ沿ＡＤ翻折，使Ｃ点落在
Ｃ
的位置，那么ＢＣ＝
 |
４．如图，已知ＰＡ切⊙Ｏ于Ａ，ＡＣ是⊙Ｏ的弦，
割线ＰＤＥ交⊙Ｏ于Ｄ、Ｅ，交ＡＣ于Ｂ，若
ＰＡ＝ＰＢ＝ＢＣ，ＰＤ＝４，ＤＥ＝２１，
则ＡＢ＝
５．如图，⊙Ａ与⊙Ｂ外切于Ｐ，ＣＤ是它们的外
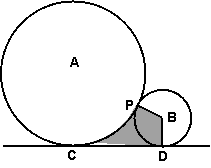公切线，切点为Ｃ、Ｄ，若⊙Ａ、⊙Ｂ的半径
Ｒ、ｒ分别是方程
的两根
（Ｒ＞ｒ），则Ｓ
＝
二、（每题５分，共１０分）
１．先花简，再求值：
已知，
，求
的值．
２．已知点Ｐ（ａ，ｂ）在函数
图象上，且ａ，ｂ是关于ｘ的方程
（ｍ－２）ｘ－２ｍｘ＋ｍ＋６＝０的两实根，其中ｍ是正整数．求直线ｙ＝－ｘ＋４与函数的图象的交点坐标．
三、（本题８分）
某电厂规定，用户用电，如果一个月用了Ａ度或Ａ度以下，每度电费为0.2元，如果一个月的电费超过了Ａ度，则超过部分每度电的电费按
元计算，其余部分仍按每度电0.2元计算．某户居民四、五月用电交费情况如下表
| 月 份 | 用电量 | 交费总数 |
| 四 | １８０度 | ３６元 |
| 五 | ２５０度 | ５６元 |
（１）四、五月用电量是否分别超过了Ａ度？为什么？
（２）求出规定的Ａ度是多少度．
四、（本题８分）
如图，已知⊙Ｏ与⊙Ｏ
外离，直线ＡＢ交⊙Ｏ于Ａ，Ｐ两点交⊙Ｏ于Ｂ，ＢＤ切⊙Ｏ于Ｄ交⊙Ｏ于Ｃ，连结ＡＣ交⊙Ｏ于Ｅ，ＰＥ延长线交ＣＤ于Ｍ，ＣＰ延长线交⊙Ｏ于Ｎ，若Ｍ是ＣＤ中点.
求证：（１）∠ＣＥＭ＝∠ＰＣＭ；
（２）ＡＰ·ＰＣ＝ＮＰ·ＰＢ
五、（本题９分）
抛物线
的顶点A在以P(1，１)为圆心，以２为半径的⊙Ｐ上，且过⊙Ｐ与ｘ轴的两个交点Ｂ、Ｃ．
（１）求抛物线的解析式
（２）求⊙Ｐ上劣弧ＡＣ的长
（３）试问在抛物线上是否存在一点Ｄ，使线段ＡＯ与ＰＤ互相平分，若存在，求出点Ｄ的坐标，若不存在，说明理由
A卷答案
一、CDBBD ABCCD BDCAB
二、1. 原式=
－2
2. 原式=
，当x=－ 时=－
三、1．证明：∵AB=AC AD⊥BC于D
∴∠BAD=∠CAD
∵BE=CF
∴AE=AF
又∵AD是公共边
∴△AED≌△AFD
∴ED=CF
2． 解：过C作CD⊥AB于D
AC=36×
=24
由题意可知∠CAB=45°∠B=30°
在RT△ACD中CD=12
在RT△BCD中BC=2CD=24
答：此时船与灯塔的距离是24海里。
四、解：设甲的速度为x公里/小时，则有：
－
=
解得：x=14
答略。
五、（1）连结AC、BC，证∠BAC=∠DAC
（2）∵EC=EB·EA ，CD=DF·DA
EB·AD=DF·AE
∴EC·CD=（EB·DA）
∴EC·CD= EB·DA
B卷答案
１．－
；２．Ｋ＝－６；３．２；４．９；５．１２－６π．
二、１．－
；２．ｍ＝１，３．当ｍ＝１时，交点是（2+，2－）
或（2－，2+）当ｍ＝３时，无交点．
三、（１）四月没超过，五月超过了．（２）规定的Ａ度是２００度．
四、（１）证到ＭＣ＝ＭＥ·ＭＰ，得到△ＣＥＭ∽△ＰＣＭ，得∠ＣＥＭ＝∠ＰＣＭ
（２）连ＡＮ，证明∠ＰＣＭ＋∠ＣＮＡ＝１８０°，得ＡＮ∥ＭＢ，
∴ＡＰ·ＰＣ＝ＮＰ·ＰＢ
五、（１）
（２）
（３）存在．四边形ＡＰＯＤ应为平行四边形，Ｄ（０，２）
 | |||
| |||