初三中考模拟考试
一、选择题（本大题共10小题；每小题4分，共40分）．在题后给出的四个选项中只有
一项是符合题目要求的，把所选项前的字母填在题后括号内
1、在
中，有理数的个数是 （ ）
（A）2 （B）3 （C）4 （D）5
2、关于
的一元次方程
有一根是0，则 m的值是（ ）
（A）
或
（B）
或
（C） （D）
3、水果店用1000元购进一批草霉，当大售出，获利10％，过几天后又以上次售出价的
90％购进同样的草霉，由于大气变化卖不出去，一天后将这批草霉按第二次购进价的
九折（即90％）降价售出．这样、这家水果店在这两次交易中（ ）
（A）赢亏平衡 （B）赢利1元 （C）赢利9元 （D）亏本1.1元
4、若点
都是反比例函数
图象上的点，且
，则下列各式中正确的是（ ）
（A）
（B）
（C）
（D）
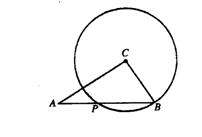
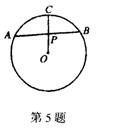5、如图，如果弦AB经过⊙O的半径OC的中点P，且PA=3，PB＝4，那么⊙O的半径等于（ ）
（A）2 （B）3 （C）5 （D）4
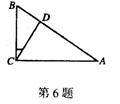
6、如图，在Rt
ABC中，
，CD
AB于点D，BC＝3，AC＝4，设
那么
的值是（ ）
（A）
（B）
（C）
（D）
7、不用查表，就可以估计出
的数值在（ ）
（A）42~43之间 （B）43~44之间 （C）44~45之间 （D）45~46之间
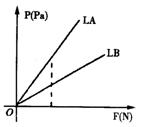8、两个受力面积分别为为常数
为常数）的物体A、B，它们所受压强
与压力F（N） 的函数图象是射线
，如图，则（ ）
（A）
（B） （C）
（D）
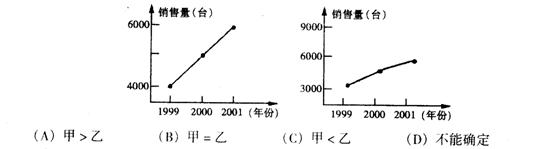
9、合肥“商之都”家电部，把甲、乙两种品牌的空调连续三年的销售情况制成不同的两种图（如下图），从图中可以看出两种品牌的空调销售量的增幅（ ）
10、如图所示，共产品的商标由三个半径都等于R的半圆两两外切得到的图形的一部分，则切点问的弧所围成的阴影部分的面积是（ ）
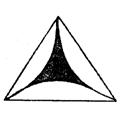（A）
（B）
（C）
（D）
二、填空题（本题共5个小题，每小题4分，共20分）
11、纳米是0.米，流感病毒的直径是90纳米，用科学记数法表示是______米．
12、如果四边形的两条对角线的长的和为10，那么顺次连结这个四边形各边中点所得的
四边形的周长为_____
13、已知一元二次方程
的两根之和与两根之积都等于10，则
14、用一张面积是S的距形纸片，将对边重合围成圆柱，能得到一高一矮两个圆柱，它们的侧面积分别为
，那么
的数量关系是______。
15、函数
的图象通过P（2，3）点，且与函数
的图象关于y轴对称，那么它们的解析式
三、（本题共2小题，每小题吕分，共16分）
16、解不等式，并把它的解集在数轴上表示出来：
17、已知直线
．
（1）求已知直线与y轴交点A的坐标；
（2）若直线与已知直线
关于y轴对称，求k与b．
四、（本题共2小题，每小题10分，共20分）
18、用换元法解方程
19、某公司进行股份制改造，设内部职工股M股，计划由公司职工平均投资入股．如果
职工中有4人愿意投资10万元，那么其余的职工平均每人可以少投资0.5万元；如
果职工中有6人愿意每人投资12万元，那么其余的职工平均每人可以少投资1万元．
如果职工中有10人不参加投资人股，那么其余的职工平均每人需投资多少万元？
五、（本题共二小题，每小题8分，共16分）
20、如图，已知 RtABC中，
，BC=1,若以C为圆心，CB长为半径的圆交AB于P，求AP的长．
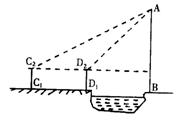21、如图，湖对岸有一电视塔AB，为测量它的高度，在
处用测角仪测得塔尖A的仰角为
，沿着塔的方向前进40米，到
处测得塔尖A的仰角为
，已知测角仪高
米，求电视塔的高（不取近似值）．
六、（本题满分12分）
22、某班有男同学27名，女同学21名，在一次语文测验中，男同学的平均分是82分，中位数是76；女同学的平均分是80分，中位数是80分．
（1）求这次测验全班平均分（精确到0.1分）
（2）估计全班成绩在80分以下（包括80分）的同学有多少人？
七、（本题满分12分）
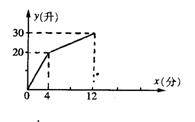
23、“海棠牌”电热水器，每单位时间内进出水的水量都是一定的，设从某一时刻开始4分钟内只进冷水，不出热水，在随后的8分钟内既进冷水又出热水，如果时间（分）与水量
（升）之间的函数关系如图所示．
（1）每分钟进水多少？
（2）当
时，与y有何关系？
（3）若12分钟后只放热水，不进冷水，求y的表达式，并在图中把相应的图象补充完整．
八、（本题满分14分）
24、如图，⊙O表示一圆形纸板，根据要求，需通过多次剪裁，把它剪成若干个扇形面，操作过程如下：第一次剪裁，将圆形纸板等分为4个扇形；第二次剪裁，将上次得到的扇形面中的一个再等分成4个扇形；以后按第2次剪裁的作法进行下去．
（1）请你在⊙O中，用尺规作出第2次剪裁后得到的7个扇形（保留痕迹，不写作法）
（2）请你通过操作和猜想，将第3、第4和第n次剪裁后所得扇形的总个数（s）填人下表．
（3）请你推断，能不能按上述操作过程，将原来的圆形纸板剪成33个扇形？为什么？
