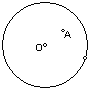初三数学第一学期期末质检复习题
一、 填空题(本大题共12小题,每题3分,计36分)
1、点P(-3,-4)到x轴的距离是 。
2、函数![]() 的自变量x的取值范围是
。
的自变量x的取值范围是
。
3、Rt△ABC中,∠A是锐角,且sinA=![]()
![]() ,则cosA=
,则cosA=
4、分解因式:2x2-3x-1= ;
5、边长为6的等边三角形的外接圆半径为
6、圆内接梯形中一内角为48°,则其余三个内角度数为 。
7、若一次函数![]() 的图象经过第一、二、四象限,则m的范围是
。
的图象经过第一、二、四象限,则m的范围是
。
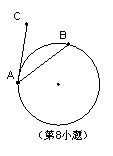 8、如图,AB是⊙O的弦,AC切⊙O于点A,且∠BAC=45°,AB=2cm,则⊙O的面积为
。
8、如图,AB是⊙O的弦,AC切⊙O于点A,且∠BAC=45°,AB=2cm,则⊙O的面积为
。
9、弓形的弦长为6cm,高为2cm,则这个圆的半径为 。
10、以AB为底边的等腰三角形的顶点C的轨迹为 ;
11、用换元法解方程![]() ,若设
,若设![]() ,则原方程可化为关于y的一元二次方程是
。
,则原方程可化为关于y的一元二次方程是
。
|
① ;
② ;
③ 。
二、 选择题(本大题共6小题,每题4分,计24分)
13、函数y=2x+3与x轴、y轴的交点分别为A、B,则ΔABC的面积为 ( )
A.![]() B.
B. ![]() ; C. 6 ; D 3 ;
; C. 6 ; D 3 ;
14、若两圆至少有两条外公切线,则这两圆的位置关系不可能是( )
A、相交 B、外离 C、内切 D、外切
15、已知点D是△ABC的内心,∠BDC=125°,则∠A=( )
A、55° B、70° C、65° D、80°
16、下列方程中,没有实数根的是… ……………………………………( )
A、![]() B、
B、![]()
|
17、、如图,已知点A是半径为5的⊙O内一点,且OA=3。过点A
且长小于8的弦有( )
A、0条 B、1条 C、2条 D、4条
18、早晨,小强从家出发,以v1的速度前往学校,途中在一饮食店吃早点,之后以v2的速度向学校行进,已知v1>v2,下面的图象中表示小强从家到学校的时间t(分)与路程s(千米)之间的关系是图中的( )
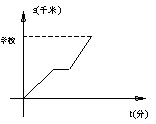
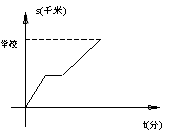 、
、
A B


C D
三、 解答题(本大题共10小题,计90分)
19、本小题满分7分
解方程![]()
20、本小题满分7分
在斜边为13的Rt△ABC中,∠C=900,三角形的面积为30,求另两边长。
21、本小题满分7分
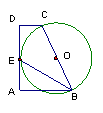 已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的圆O切AD于点E。连结BE,若BC=6,∠EBC=30°,求梯形ABCD的面积。
已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的圆O切AD于点E。连结BE,若BC=6,∠EBC=30°,求梯形ABCD的面积。
22、本小题满分7分
已知AB(用尺规作图,不写作法,要求保留作图痕迹)
 求作:(1)确定AB的圆心O;
求作:(1)确定AB的圆心O;
(2)过点A作圆O的切线。
23、本小题满分8分
甲、乙两人(甲骑自行车,乙骑摩托车)从A
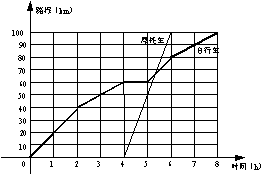 城出发到B城旅行,如右图表示甲、乙两人离开A
城出发到B城旅行,如右图表示甲、乙两人离开A
城的路程与时间之间的函数图象。根据图象,你能得到关于甲、乙两人旅行的哪些信息?
说明:⑴请至少提供4条信息,比如,由图可知:甲比
乙早出发4小时;甲离开A城的路程与时间之间的函数图象是一条折线,说明甲作变速运动;…等等
⑵请不要再提供如⑴的一些信息。
⒈
⒉
⒊
⒋
24、本小题满分8分
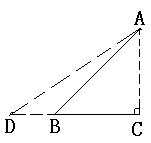
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为12m,它的坡角为45o,为了提高该堤的防洪能力,现把它改成坡比为![]() 的斜坡AD. 求DB的长(结果保留根号).
的斜坡AD. 求DB的长(结果保留根号).
25. 本小题满分10分
已知关于x 的方程x2+2(2-m)x+3-6m=0
(1) 请你判断–3是否是方程的根;
(2) 如果方程的两个实数根x1、x2满足x1=3x2,求实数m的值.
26、本小题满分10分
已知,两等圆⊙O1、⊙O2相交于A、B两点,且两圆互过圆心,且过B任作一直线,分别交于两圆于C、D两点,连接AC、AD。
(1)
当AB![]() CD时,试判断ACD的形状,并给出证明;
CD时,试判断ACD的形状,并给出证明;
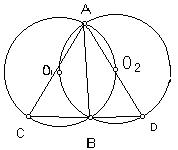
(2) 当AB与CD不垂直时,(1)中你得到的结论还成立吗?说明你的理由。
27、本小题满分12分
已知:在△ABC中,AD为∠BAC的平分线,以C为圆心,CD为半径的半圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,FE:FD=4:3。
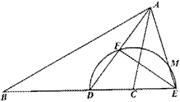 (1)求证:AF=DF;
(1)求证:AF=DF;
(2)求∠AED的余弦值:
 28、本小题满分12分
28、本小题满分12分
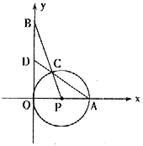
如图,⊙P与y轴相切于坐标原点O,点A(2,0)是⊙P与x轴的交点,点B(0,2![]() )在y轴上,连结BP交⊙P于点C,连结AC并延长交y轴于点D。
)在y轴上,连结BP交⊙P于点C,连结AC并延长交y轴于点D。
(1)求线段BC的长;
(2)求直线AC的函数解析式;
(3)当点B在y轴上移动时,存在着点B,使△BOP相
似于△AOD,试求出符合条件的点B的坐标。
参考答案
一、1.4 2.x≧-1且x≠0 3.![]() 4.
4. ![]() 5.
5.![]() 6.48°、132°、132° 7.m>2 8.2
6.48°、132°、132° 7.m>2 8.2![]() (平方单位) 9.
(平方单位) 9.![]() 10.线段AB的垂直平分线(扣除AB中点) 11.2y2-5y+2=0 12.①AC=CD ②CB=BD ③△CBD∽△ACD
10.线段AB的垂直平分线(扣除AB中点) 11.2y2-5y+2=0 12.①AC=CD ②CB=BD ③△CBD∽△ACD
二、13.B 14 C 15.B 16.A 17.A 18.A
三、19. X=1或x=-3
20.解:设另两边长为![]()
∴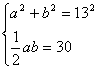 ∴
∴![]()
∴![]() 是一元二次方程,
是一元二次方程,![]() 两根
两根
解得:方程两根为5,12
∴另两边长为5,12
21.解:![]()
22.确定圆心4分,作切线3分
23.评价:文字说明或建立表达式均可
24.解:在Rt△ABC中,
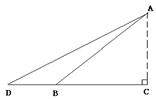
![]()
Rt△ADC中,
![]()
答:DB的长为![]() .
.
25.解:(1)代入检验,-3是原方程的根
(2)设另一根为![]()
∴![]() (-3)=3(1-2m)
(-3)=3(1-2m)
∴![]() =2m-1
=2m-1
当x1=-3,x2=2m-1时,有
-3=3(2m-1)
得m=0
当x1=2m-1 x2=-3时,有
2m-1=3×(-3)
得 m= -4
∴m的值为0,-4
26.(1)答:△ACD是等边△
证明: ∵AB⊥CD
∴AC、AD分别为两圆直径
∴AC=AD O2在AB上
又连结CO2
∴CO2⊥AD且CO2平分AB
∴CA=CD
∴AC=AD=CD
∴△ACD仍是等边三角形
(2)答:结论依然成立
事实上,由同孤所对的圆周角相等知
∠C、∠D的大小不变,都等于60°
∴△ACD是等边三角形
∴结论保持不变
注:(1)中的证法是非本质的,可连接01A、01B、02A、02B 0102,由此证明两圆的弧AB的度数为120°,这样不难得到![]() 是等边三角形。解题中应注意养成从特例直观猜测—验证—进一步思考一般性结论—反思解法——揭示本质的思维活动过程。
是等边三角形。解题中应注意养成从特例直观猜测—验证—进一步思考一般性结论—反思解法——揭示本质的思维活动过程。
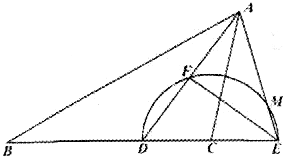 27、(1)证明:∵AD平分∠BAC
27、(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAC
∵∠B=∠CAE
∴∠BAD+∠B=∠DAC+∠CAE
∵∠ADE=∠BAD+∠B
∴∠ADE=∠DAE
∴EA=ED
∵DE是半圆C直径
∴∠DFE=90°
∴AF=DF…………………………………………………………………2分
(2)解:连结DM
∵DE是半圆C的直径
∴∠DME=90°
∵FE:FD=4:3
∴可设FE=4x,则FD=3x
由勾股定理,得DE=5x
∴AE=DE=5x ,AF=FD=3x
由切割线定理的推论,得AF·AD=AM·AE
∴3x(3x+3x)=AM·5x
∴AM=![]()
∴ME=AE-AM=5x-![]() =
=![]()
在Rt△DME中,
∴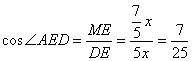 ……
……
28、解:(1)由条件知OB=2![]()
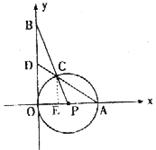 OA=2,OP=1
OA=2,OP=1
∴BP=![]() ………………2分
………………2分
∵OP=PC=1
∴BC=BP-PC=3-1=2 …………………3分
(2)过点C作x轴的垂线CE,垂足是E
∴CE∥BO
∴![]()
∴CE=![]() ,PE=
,PE=![]()
∴OE=1-![]() =
=![]()
∴C(![]() ,
,![]() )而A(2,0) ………………………………4分
)而A(2,0) ………………………………4分
设直线AC的解析式是y=kx+b
![]() 2k+b=0
2k+b=0
|
∴k=﹣![]() ,b=
,b=![]()
∴直线AC的解析式是y=﹣![]() x+
x+![]() …………………………6分
…………………………6分
(3)在y轴上存在点B,使△BOP∽△AOD ……………………7分
理由如下:∵∠BOP=∠AOD=Rt∠
∴当∠OBP=∠OAD时,△BOP∽△AOD
∵∠OAC=![]() ∠OPC
∠OPC
∴∠OBP=![]() ∠OPB
∠OPB
∵∠OBP+∠OPB=90°
∴∠OBP=30° …………………………………………8分
∵OP=1
∴OB=OPcot∠OBP
=1×cot30°
=![]()
∴B(0,![]() )
)
由对称性知,符合条件的点共有两个,分别为B1(0,![]() ),B2(0,﹣
),B2(0,﹣![]() )……9分
)……9分